Темы --> Информатика --> Алгоритмы --> Задачи на моделирование
---> 2 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников --> Окружная олимпиада
    2006(6 задач)
    2007(6 задач)
    2008 (четвертый интернет-этап)(6 задач)
Страница: 1 Отображать по:
#598
Маджонг
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Петя недавно узнал о существовании игры маджонг. Она ему показалась настолько интересной, что он играет в нее целыми днями. Для этой игры необходима прямоугольная доска размером m  n полей и набор фишек разных цветов. При этом фишек каждого цвета в наборе должно быть ровно две. В начале игры фишки располагаются на доске произвольным образом.

После этого за один ход разрешается снять пару фишек одного цвета, если они обе являются самыми правыми в своих горизонталях, либо самыми левыми в своих горизонталях, либо самыми нижними в своих вертикалях, либо самыми верхними в своих вертикалях. Если соответствующей пары фишек нет, то игра закончена.

Например, на рисунке показан пример позиции в игре, когда можно сделать два хода: снять две фишки четвертого цвета, поскольку они являются самыми левыми в своих горизонталях, либо снять две фишки первого цвета, поскольку они являются самыми верхними в своих вертикалях.

Цель игры состоит в том, чтобы сделать как можно больше ходов.

Задана начальная расстановка фишек на доске. Требуется найти самую длинную последовательность ходов, которую может сделать Петя из заданной позиции.

Входные данные

Первая строка входного файла содержит размеры доски: два целых числа \(m\) и \(n\) (1 ≤ \(m\), \(n\) ≤ 300, хотя бы одно из этих чисел четно). Далее следуют \(m\) строк по \(n\) чисел в каждой, \(j\)-е число в \(i\)-й из этих строк представляет собой номер цвета \(j\)-й слева фишки в \(i\)-й горизонтали. Цвета пронумерованы натуральными числами от 1 до \(n\)*\(m\) / 2. На доске ровно две фишки каждого цвета.

Выходные данные

В первой строке выходного файла выведите \(k\) — максимальное количество ходов, которое может сделать Петя из заданной начальной позиции. Во второй строке выходного файла выведите разделенные пробелами \(k\) чисел — номера цветов фишек в том порядке, в котором они должны сниматься с доски. Если возможных ответов несколько, выведите любой.

Примеры
Входные данные
1 2
1 1
Выходные данные
1
1
Входные данные
4 1
1
2
2
1
Выходные данные
2
2 1
#1155
Трехмерный тетрис
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Игра в трехмерный тетрис происходит на поле, имеющем вид прямоугольного параллелепипеда размером W×D×H единичных кубиков. Введем координатную систему так, чтобы один из углов параллелепипеда находится в точке (0, 0, 0), противоположный ему – в точке (W, D, H), а ребра параллелепипеда были параллельны осям координаты. Каждый единичный кубик поля можно задать максимальными координатами его углов, тогда кубики будут иметь координаты от (1, 1, 1) до (W, D, H).

В процессе игры на поле последовательно появляются фигуры. Каждая фигура представляет собой множество единичных кубиков и обладает следующим свойством: от любого кубика можно добраться до любого другого, переходя через общую грань.

Игрок может сделать несколько действий с фигурой. Каждое действие является либо перемещением ее на один в направлении одной из осей координат, либо поворотом ее на 90 градусов вокруг одной из координатных осей. Один из кубиков в фигуре является базовым – при поворотах он остается на месте. При повороте фигура сначала исчезает с игрового поля, и затем появляется снова, уже в новом положении. Направления поворотов показаны на рисунке, при повороте вокруг оси OX ось OY переходит в ось OZ, при повороте вокруг оси OY ось OZ переходит в ось OX, при повороте вокруг оси OZ ось OX переходит в ось OY. Базовый кубик при повороте остается на месте.

 

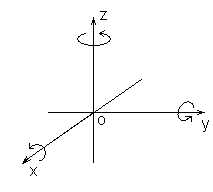Требуется написать программу модуля, ответственного за определение кубиков, которые в результате игры окажутся заняты фигурами. Заранее известна последовательность появления фигур на поле и действия с этими фигурами, которые произвел игрок. Гарантируется, что каждое из действий допустимо, то есть не происходит выхода фигуры за границу поля, и не происходит появления у двух фигур общего кубика.

Входные данные

В первой строке входного файла содержатся размеры игрового поля – три целых числа W, D и H (1 ≤ W, H, D ≤ 100).

Во второй строке входного файла задано целое число n – количество фигур, которые были размещены на игровом поле. (0 ≤ n ≤ 100). Каждая фигура задается следующим образом: на первой строке задано натуральное число m - количество кубиков в фигуре. (1 ≤ m ≤ 100) Далее следуют m строка, в i-й из которых содержится тройка целых чисел xi, yi, zi – координаты i-го кубика в фигуре в ее начальном положении. Базовый кубик описывается первым.

Следующая строка содержит целое число k – количество операций, которые были проведены игроком с данной фигурой (0 ≤ k ≤ 100). Далее следуют k строк. Каждая из них начинается либо со слова «shift», либо со слова «rotate».

В первом случае далее следует одна из букв «x», «y» или «z», обозначающая, вдоль какой из осей был выполнен сдвиг, после чего через пробел идет либо символ «+», если сдвиг был осуществлен в положительном направлении данной оси, либо «–», если сдвиг был осуществлен в отрицательном направлении.

Если же строка начинается со слова «rotate», то далее идет одна из букв «x», «y» или «z», обозначающая, вокруг какой из осей был выполнен поворот.

Выходные данные

Выведите в выходной файл в произвольном порядке координаты всех кубиков, которые будут заняты фигурами. На каждой строке должно содержаться три числа, разделенных пробелом – координаты кубика в формате «x y z».

Примеры
Входные данные
2 2 2
1
2
1 1 1
2 1 1
1
shift z +
Выходные данные
2 1 2
1 1 2
Входные данные
3 3 3
1
4
2 2 2
3 2 2
2 3 2
2 2 3
2
rotate y
rotate z
Выходные данные
2 2 2
2 3 2
2 2 1
1 2 2
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест