#1047

Праздники

Темы: [Массивы]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2004, 1 день, Задача A ]

На планете в звездной системе Альфа Кентавра неделя состоит из A дней, а год - из B дней. Годы нумеруются последовательными натуральными числами: 1, 2, 3, ... Кроме того, годы с номерами C₁, C₂, ..., C_N являются високосными и состоят из (B+1) дней. В году дни с номерами D₁, D₂, ..., D_M являются праздничными. Если праздник попадает на (B+1)-й день года, то он отмечается только в високосные годы. Первый день первого года является первым днем недели.

Один из жителей планеты решил устроиться на новую работу. В соответствии с заключенным трудовым договором он будет числиться на данной работе в течение E дней, начиная с первого дня 1-го года. По договору он имеет право выбрать один день недели (с 1 по A), который будет для него выходным. Праздничные дни также считаются нерабочими. Житель хочет выбрать себе выходной день таким образом, чтобы за период действия договора у него было максимальное количество нерабочих дней.

Требуется написать программу, которая определяет искомый день недели и вычисляет соответствующее количество нерабочих дней.

Входные данные

В первой строке входного файла через пробел записаны числа A и B - количество дней в неделе и в невисокосном году соответственно (1 ≤ A ≤ 2500, 1 ≤ B ≤ 10000). Во второй строке записано число N - количество високосных лет, и в третьей - номера C₁, C₂, ..., C_N високосных лет в возрастающем порядке (0 ≤ N ≤ 5000, 1 ≤ C₁ < C₂ < ... < C_N ≤ 10⁷). В следующей строке число M - количество праздничных дней в году, и на новой строке - D₁, D₂, ..., D_M в возрастающем порядке (1 ≤ D₁ < D₂ < ... < D_M ≤ B+1). В последней строке записано число E (1 ≤ E ≤ 10⁹). Известно, что житель заключил контракт не более чем на 10⁷ лет.

Выходные данные

В выходной файл выведите через пробел два числа - номер дня недели, который выгоднее всего сделать выходным, и соответствующее количество нерабочих дней за период действия договора. Если ответов несколько, то выведите любой из них.

Примеры

Входные данные

Выходные данные

1 8

#1048

Опечатки

Темы: [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2004, 1 день, Задача B ]

При наборе текста довольно часто возникают опечатки из-за неправильного нажатия на клавиши. Например, некоторые буквы оказываются заменены на другие, появляются лишние буквы, некоторые буквы исчезают из слов. В большинстве случаев эти опечатки можно исправить автоматически. В частности, существует метод проверки орфографии, основанный на поиске в словаре слов, похожих на проверяемые.

Два слова называются похожими, если можно удалить из каждого слова не более одной буквы так, чтобы слова стали одинаковыми, возможно пустыми. Например, слова "spot" и "sport" похожи, так как одно и то же слово "spot" можно получить из первого слова без удаления букв, а из второго - удалением буквы "r".

Требуется написать программу, которая для каждого слова проверяемого текста определяет количество похожих на него слов в словаре.

Входные данные

В первой строке входного файла через пробел записаны натуральные числа N ≥ 1 - общее количество слов в словаре и M ≥ 1 - количество слов в проверяемом тексте (N+M ≤ 20000) В последующих N строках записаны слова, входящие в словарь, по одному на строке. Все слова словаря различны. Далее следуют M строк, в которых записаны слова проверяемого текста, по одному слову в строке.

Слова состоят из строчных и прописных букв латинского алфавита (прописные и строчные буквы считаются различными). Любое слово состоит не менее чем из одной и не более чем из 12 букв.

Выходные данные

Для каждого слова из текста выведите в выходной файл строку, содержащую это слово, далее через пробел количество слов из словаря, на которые оно похоже. Если в словаре имеется единственное похожее слово, то также выведите в этой строке это слово (через пробел).

Примеры

Входные данные

5 8
father
and
or
mother
a
Father
and
mather
go
o
for
e
walk

Выходные данные

Father 1 father
and 1 and
mather 2
go 1 or
o 2
for 1 or
e 1 a
walk 0

#1049

Горнолыжные соревнования

Темы: [Элементарная геометрия] [Дерево Фенвика] [Дерево отрезков, RSQ, RMQ]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2004, 1 день, Задача C ]

Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.

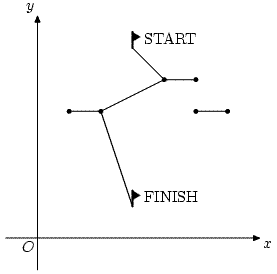
Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.

За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.

Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.

Входные данные

В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы S_x, S_y, F_x, F_y - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа a_i, b_i, y_i, c_i - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (a_i < b_i, F_y < y_i < S_y, c_i - целое число, 0 ≤ c_i ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.

Выходные данные

В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.

Система оценки

Потестовая.

Примеры

Входные данные

Выходные данные

7.8126