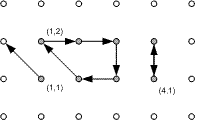
На плоскости задано множество точек (x, y), где x, y – целые числа, 1≤x≤M, 1≤y≤N. Из каждой точки выходит ровно один из следующих векторов: (-1,-1), (-1,0), (-1,1), (0,1), (1,1), (1,0), (1,-1), (0,-1). Каждый вектор соединяет одну целочисленную точку плоскости с другой. Например, если из точке (2, 5) выходит вектор (1, 1), то он соединяет эту точку с (3, 6), но не наоборот.
Последовательность из двух и более точек плоскости a1, a2,…, ak назовем циклом, если каждая точка ai соединена вектором с ai+1 (1≤i≤k-1), и ak соединена вектором с a1. Циклы считаются разными если они отличаются хотя бы одной вершиной.
Напишите программу, которая по информации о векторах, выходящих из точек плоскости, находит количество различных циклов.
Первая строка входного файла содержит два целых числа N (1≤N≤100) и M (1≤M≤100). Каждая из последующих N строк, содержит M пар чисел (т.е. 2≤M чисел). Пара x, которая находится в строке y, задает вектор в точке (x, y).
Единственная строка выходного файла должна содержать целое число – количество циклов, образованных векторами.
2 4 -1 1 -1 1 -1 0 0 1 1 0 1 0 0 -1 0 -1
2
Система рейсов авиакомпании OlympAirways была спроектирована таким образом, чтобы из любого аэропорта, который обслуживается авиакомпанией, можно было перелететь в любой другой аэропорт, воспользовавшись, возможно, больше чем одним рейсом. Каждый рейс соединяет два аэропорта, и выполняется в обе стороны.
Существует проблема, что некоторые рейсы определенное время могут не выполняться из-за плохих погодных условий. Таким образом, вероятно, что клиент не сможет перелететь из аэропорта A аэропорт B, пользуясь только самолетами авиакомпании OlympAirways. Для исследования подобных ситуаций научный отдел компании ввел понятие числа уязвимости связи между парой аэропортов A и B. Это число равно количеству рейсов авиакомпании, отмена любого из которых (при условии, что все остальные рейсы выполняются в обычном порядке) приведет к невозможности перелета в аэропорт B из аэропорта A.
Напишите программу, которая по информации обо всех рейсах, выполняемых авиакомпанией, определяет сумму чисел уязвимости связи между всеми парами аэропортов.
Первая строка входного файла содержит целое число N (1≤N≤100) – количество аэропортов, которые обслуживаются авиакомпанией. Вторая строка содержит целое число M (1≤M≤4950) — количество рейсов, выполняемых авиакомпанией. Каждая из последующих M строк задает рейс, который представлен парой целых чисел от 1 до N – номерами аэропортов, которые он соединяет.
Единственная строка выходного файла должна содержать целое число — суммарное число уязвимости связи между всеми разными парами аэропортов A и B, таких, что номер A меньше номера B.
5 5 1 2 4 2 4 5 3 2 3 1
10
Наверное, всем известно, что шоколад полезен для мозга человека. Поэтому участники национальной олимпиады страны Олимпия принесли на тур много плиток шоколада, чтобы гениальные идеи приходили к ним быстрее. Однако принесенного шоколада оказалось слишком много, и после тура в кабинете осталось N прямоугольных плиток, которые состояли из долей размерами 1×1. Двое участников решили съесть часть оставшегося шоколада, но, учитывая что во время тура они уже съели достаточно много шоколада, было решено сделать это достаточно необычным игровым способом, по следующим правилам.
Участники выполняют определенные операции с шоколадными плитками по очереди: сначала первый, потом второй, снова первый и т.д. В свою очередь участник выбирает плитку шоколада, с которой он будет выполнять одну из следующих операций:
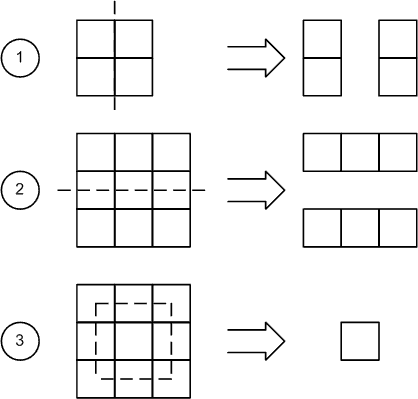
- Разломить плитку на две; линия разлома должна проходить параллельно сторонам плитки и между долями.
- Отломить и съесть произвольную «строку» или «столбик» плитки, который не есть крайним.
- Отломить и съесть все доли плитки, которые находятся с краю, но чтобы после этого от плитки осталась хотя бы одна доля (минимальный размер плитки, c которой может быть произведена такая операция – 3×3)
Никакая из этих операций не может быть произведена с плиткой 1×1, поэтому все такие плитки остаются до конца игры. Проигрывает тот участник, который в свою очередь не может произвести ни одной из приведенных операций.
Напишите программу, которая по информации о плитках шоколада, оставшихся после тура, определяет количество вариантов первого хода первого участника, гарантирующих ему выигрыш, при следовании выигрышной стратегии в дальнейшем.
В первой строке входного файла содержится целое число N (1≤N≤100) – количество шоколадных плиток. Во второй строке содержатся N пар целых чисел, каждая i-ая из которых задает длину и ширину i-ой плитки. Длина и ширина не меньше чем 1 и не превышают 100.
В единственной строке выходного файла должно находиться целое число – количество вариантов первого хода первого участника, которые гарантируют ему выигрыш, при следовании оптимальной стратегии в дальнейшем.
Комментарий к примеру тестов
Выигрышные ходы первого участника следующие: операция (3), операция (2) со второй строкой, и операция (2) со вторым столбиком.
1 3 3
3