Как и у каждого мальчика, у Феди есть игрушечные машинки. Однако ему повезло больше, чем обычному мальчику — все \(n\) его машинок являются радиоуправляемыми. Целыми днями он может устраивать различные автогонки и играть с друзьями.
Из всех видов гонок Федя предпочитает гонки по прямой. В данном формате соревнования трасса имеет форму прямой и является бесконечной (соревнования идут до тех пор, пока Феде это не надоест). Изначально каждая из \(n\) машинок находится на некотором расстоянии от старта — имеет фору \(x_i\) метров. По команде все машинки начинают свое движение от старта, при этом каждая машинка движется во время гонки с постоянной скоростью \(v_i\) метров в секунду. Все машинки движутся в одном направлении — удаляются от старта.
Недавно Феде подарили видеокамеру, и он хочет заснять яркие моменты гонки. Прежде всего Федя хочет запечатлеть первый обгон гонки, то есть первый момент времени, в который две машины находятся на одном расстоянии от старта.
Так как этого события можно ждать очень долго, Федя хочет настроить камеру на автоматическое включение во время обгона. Однако, Федя самостоятельно не может найти время, которое пройдет со времени начала гонки до времени первого обгона. Помогите Феде — напишите программу, находящую искомую величину.
В первой строке входного файла содержится единственное число \(n\) — количество машинок на трассе (2 \(\leq\) n \(\leq\) 100). Каждая из следующих \(n\) строк содержит по два целых числа \(x_i\) и \(v_i\) — расстояние от старта (в метрах) и скорость машинки \(i\) (в метрах в секунду) соответственно (1 \(\leq x_i, v_i \leq\) 1000).
Исходно никакие две машинки не находятся в одной точке. Гарантируется, что хотя бы один обгон во время гонки произойдет.
В выходной файл выведите количество секунд, которое пройдет с момента старта до момента первого обгона, с точностью не менее 5 знаков после десятичной точки.
Пояснение для первого примера:
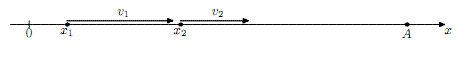
На рисунке точкой A обозначено место обгона.
2 1 3 4 2
3.00000
2 12 20 2 21
10.00000
В тактике футбола одним из основных понятий является схема игры. Она определяет, сколько из десяти полевых игроков будут играть в защите, сколько — в полузащите и сколько — в нападении.
Например, схема игры 5-3-2 означает, что в команде пять защитников, три полузащитника и два нападающих. В соответствии с современными представлениями на схему игры накладываются следующие ограничения: должно быть не менее одного и не более пяти защитников, не менее одного и не более пяти полузащитников и не более трех нападающих. Отметим, что нападающих может в команде и не быть совсем. Будем рассматривать только такие схемы.
Будем считать, что футбольное поле имеет длину 120 метров и ширину 80 метров. Введем на нем прямоугольную декартову систему координат таким образом, как показано на рисунке. Ворота рассматриваемой нами команды находятся слева.
Будем также считать, что игрок в некоторый момент времени находится в линии полузащиты, если он находится на расстоянии не более 20 метров от центральной линии. Соответственно, игрок находится в линии защиты, если он находится не более чем в 40 метрах от «своей» лицевой линии, и в линии нападения, если находится не более чем в 40 метрах от «чужой» лицевой линии.
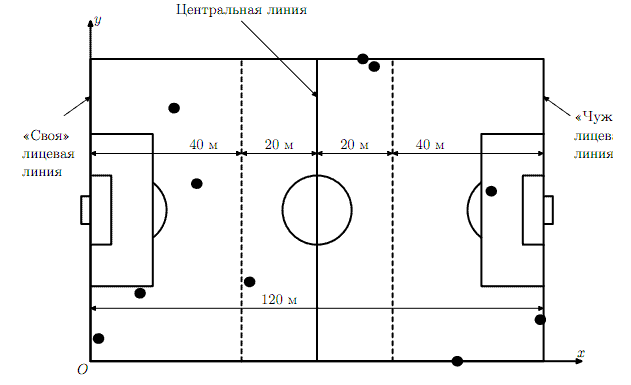
Например, в ситуации, изображенной на рисунке, в линии защиты находятся четыре игрока, в линии полузащиты — три, в линии нападения — также три.
В процессе игры некоторые игроки могут перемещаться из одной линии в другую. В этой задаче будем считать, что возможно перемещение из полузащиты в защиту (и обратно) и из полузащиты в нападение (и обратно). Таким образом, игрок, который в соответствии со схемой игры является защитником, не может оказаться в линии нападения, и наоборот — игрок, который в соответствии со схемой игры является нападающим, не может оказаться в линии защиты. Кроме этого, в соответствии с установкой тренера из каждой линии в каждую могло перейти не более двух игроков.
Ваша задача состоит в том, чтобы написать программу, которая по положениям игроков в некоторый момент времени найдет все возможные схемы игры, при которых в течение игры могло возникнуть такое расположение игроков.
Входной файл содержит десять строк, содержащих по два целых числа xi и yi каждая, — координаты каждого из игроков команды (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 ≤ yi ≤ 80).
В первой строке выходного файла выведите k — число схем игры, по которым может играть команда. В последующих k строках в произвольном порядке выведите описание каждой из этих схем. Следуйте формату данных, приведенному в примере.
97 0 13 18 2 6 119 11 42 21 72 80 75 78 106 45 22 67 28 47
9 2-5-3 3-5-2 3-4-3 4-5-1 4-4-2 4-3-3 5-4-1 5-3-2 5-2-3
В новой математической игре для одного игрока «Таблица чисел» используется таблица размером n строк на m столбцов, заполненная целыми числами. За один ход игрок выбирает одну из строк или один из столбцов и меняет знак на противоположный у всех чисел этой строки или столбца.
Цель игры состоит в том, чтобы привести таблицу в такой вид, что сумма чисел в каждой строке и каждом столбце является неотрицательной. При этом минимизировать количество ходов не требуется, но можно сделать не более 20000 ходов.
Ваша задача состоит в том, чтобы написать программу, которая по описанию начального вида таблицы, найдет последовательность ходов, которая ведет к достижению цели игры, или определит, что цель игры недостижима.
Первая строка входного файла содержит два целых числа: n и m (2 ≤ n, m ≤ 100). Каждая из последующих n строк содержит по m целых чисел a
В первой строке выходного файла выведите k — число ходов, которые необходимо выполнить, или «-1», если цели игры добиться невозможно. В первом случае в последующих k строках выведите описание этих ходов.
Описание каждого хода должно быть выведено в отдельной строке, которые должны содержать: тип хода («R» — на этом ходе выбирается строка или «C» — на этом ходе выбирается столбец) и номер соответствующей строки или столбца. Строки и столбцы нумеруются натуральными числами начиная с единицы, строки нумеруются сверху вниз, а столбцы — слева направо.
Выведенная вашей программой последовательность ходов должна содержать не более 20000 ходов. Гарантируется, что если существует последовательность ходов, ведущая к достижению цели игры, то существует и последовательность, удовлетворяющая указанному ограничению
2 2 -1 -3 1 -2
1 C 2
3 2 -1 -1 -1 -1 -1 -1
3 R 1 R 2 R 3
Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной w ячеек и высотой h ячеек. В некоторых из них расположены кнопки.
Код на этом замке вводится одновременным нажатием k кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.
Для оценки надежности замков требуется написать программу для вычисления указанной величины.
Формат входных данных
В первой строке входного файла находятся три целых числа h, w и k (1 ≤ h, w ≤ 30; 1 ≤ k ≤ 10). Каждая из последующих h строк содержит w символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.
Формат выходных данных
В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.
Примеры
| Входные данные | Выходные данные |
| 2 2 2 .# ## | 2
|
| 5 6 7 .#.... ##.##. ..#.#. .####. .....# | 3 |
На рисунке изображен один из возможных кодов для второго примера.
