Страница: << 3 4 5 6 7 8 9 Отображать по:

#113134

Передача опыта

Источники: [ Личные олимпиады, Нижегородская олимпиада школьников, XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г., Задача E ]

Как известно, Берляндия — хорошо развитая страна, а поэтому в каждом городе есть школа. На недавнем съезде учителей стало ясно, что методики преподавания различных предметов во всех школах разные. Чтобы исправить это недоразумение, а также для улучшения качества образования было решено, что школам необходимо обмениваться опытом. Так как школы действительно разные, и у каждой имеется уникальный опыт, поступило предложение из каждой школы в каждую другую отправить делегата для перенимания опыта.

К сожалению, города в Берляндии находятся далеко друг от друга, поэтому их связывает минимальная возможная сеть дорог: из каждого города можно добраться по дорогам в любой другой не посещая ни один город дважды, но при этом лишь единственным способом. Также, еще большую проблему для учителей создает сложная система оплаты проезда по дорогам Берляндии.

Каждой дорогой владеет одна из K компаний, и для проезда по дорогам любой компании человек должен один раз купить проездной у этой компании. После этого он может проезжать по любым дорогам этой компании без дополнительной платы. Стоимость проездного i -ой компании ( 1 ≤ i ≤ K ) равна c _i бурлей.

Каждому из делегатов нужно купить необходимые ему проездные. Помогите учителям посчитать, сколько же всего бурлей будут стоить все проездные для всех делегатов. Так как это число может быть большим, найдите остаток от деления этого числа на 1 000 000 007 ( 10 ⁹ + 7 ).

Входные данные

В первой строке входных данных находятся два натуральных числа N и K ( 1 ≤ N ≤ 1 500 000 , 1 ≤ K ≤ 1 500 000 ) — число городов в Берляндии и число компаний-владельцев дорог соответственно. На следующих ( N - 1) строках дано описание дорог Берляндии, на i -ой из этих строк (эти строки нумеруются с единицы, города тоже нумеруются с единицы) находятся два числа b _i и t _i ( 1 ≤ b _i ≤ N , 1 ≤ t _i ≤ K ), означающие, что существует дорога из города с номером i + 1 в город с номером b _i , и владеет ей компания с номером t _i . По всем дорогам можно передвигаться в обе стороны; также, гарантируется, что из любого города можно добраться в любой другой по существующим дорогам.

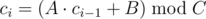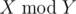На последней строке входных данных находятся 4 числа A , B , C , c ₀ ( 1 ≤ C ≤ 1 000 000 001 , 0 ≤ A , B , c ₀ < C ), задающие стоимости проездных. Стоимости проездных вычисляются по формуле $\text{[math]}$ , где c _i "— стоимость проездного i -ой компании, а « $\text{[math]}$ » — остаток от деления X на Y .

Выходные данные

Выведите единственное число — остаток от деления суммарной стоимости необходимых проездных на 1 000 000 007 .

Примечание

$\text{[math]}$

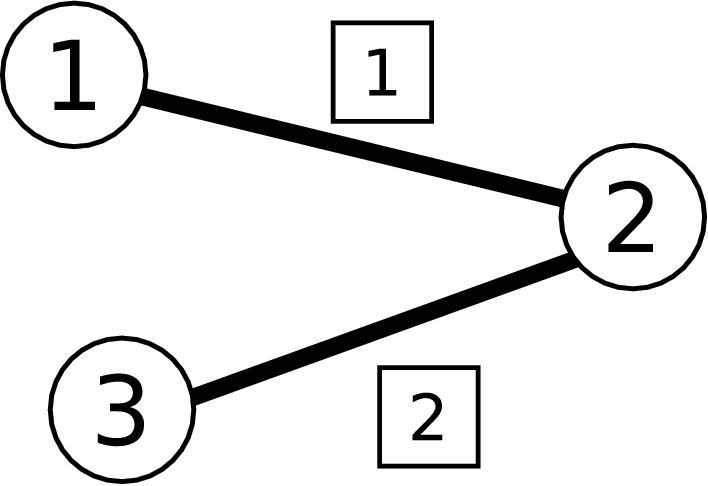
В первом тесте из примера карта дорог выглядит так, как показано на рисунке. Кружками обозначены города, линиями — дороги, а числа в квадратах около дорог обозначают номера компаний, обслуживающих эти дороги. Цены проездных в этом примере равны c ₁ = 3 бурля, c ₂ = 5 бурлей. Таким образом, делегаты, едущие из первого города в третий, или обратно, должны купить оба проездных, остальным делегатам нужно проехать только одну дорогу, поэтому им нужно купить только один проездной. Итоговая стоимость проездных равна 2·(3 + 5) + 2·3 + 2·5 = 32 бурлей.

Во втором тесте схема дорог выглядит так же, а компания-владелец только одна. Стоимость проездного равна 3 бурля. Поэтому все 6 делегатов должны купить единственный проездной, и суммарная стоимость 6·3 = 18 бурлей.

Тесты, в которых выполняются дополнительные ограничения 1 ≤ N , K ≤ 100 , имеют суммарную стоимость не менее 30 баллов.

Тесты, в которых выполняются дополнительные ограничения 1 ≤ N , K ≤ 1000 , имеют суммарную стоимость не менее 50 баллов.

Тесты, в которых выполняются дополнительные ограничения 1 ≤ N , K ≤ 100 000 , имеют суммарную стоимость не менее 75 баллов.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#113135

Источники: [ Личные олимпиады, Нижегородская олимпиада школьников, XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г., Задача F ]

Вы — министр транспорта в Тридевятом королевстве. Дороги, как известно, являются одной из основных проблем королевства, тем не менее, недавно была закончена постройка Великого Королевского Тракта — самой длинной дороги в Тридевятом царстве. Тракт представляет из себя прямую дорогу, поэтому далее будем называть координатой точки на тракте расстояние от начала тракта до нее.

Вам стало известно, что король скоро собирается проехать по этому тракту от начала до конца, причем поедет он со скоростью 1. Когда именно он собирается начать, вам неизвестно, но зато вы уверены, что это произойдет в какой-то случайный целочисленный момент времени между t ₁ и t ₂ включительно. В рамках модернизационной программы вы отдали поручение построить на Тракте n светофоров, которые должны будут впечатлить проезжающего короля. Светофоры в некотором смысле одноразовые, а именно они поначалу горят зеленым, затем красным, а потом снова зеленым, не переключаясь больше, пока не сломаются (но можно считать, что сломаются они не скоро). Про каждый светофор вам известно три величины: его положение на Тракте, время, когда он загорится красным, и время, когда он вновь загорится зеленым. Так получилось, что последний светофор стоит прямо на конце Тракта. Понятно, что король не станет подавать плохой пример подданным: никакой светофор он не будет проезжать на красный свет (в том числе это относится и к последнему светофору). В момент, когда красный свет только загорается, ехать уже становится нельзя, а когда загорается зеленый — сразу же можно.

Ваша премия как министра напрямую зависит от того, насколько долго король будет ехать по тракту, поэтому вас интересует вопрос, сколько в среднем времени ему потребуется на то, чтоб проехать Тракт от начала до конца (включая время ожидания на последнем светофоре, если это потребуется). Напишите программу, которая посчитает эту величину.

Входные данные

В первой строке входного файла вводится число n — количество светофоров ( 1 ≤ n ≤ 100 000 ). Затем в каждой из следующих n строк — описания светофоров. В каждой из них содержатся 3 целых числа x _i , s _i , f _i ( 0 ≤ x _i , s _i , f _i ≤ 10 ⁹ ), описывающих очередной светофор: x _i — это положение светофора на Тракте, s _i — момент времени, когда светофор загорится красным, f _i — момент времени, когда он вновь загорится зеленым ( 0 ≤ s _i < f _i ). Светофоры упорядочены по величине x , т.е. для любых номеров i и j таких, что 1 ≤ i < j ≤ n , верно, что x _i < x _j . Кроме того, гарантируется, что длина Тракта больше нуля, т.е. что x _n > 0 .

В последней строке задаются целые числа t ₁ и t ₂ — начальный и конечный момент времени, когда король может начать свой путь ( 0 ≤ t ₁ ≤ t ₂ ≤ 10 ⁹ ).

Выходные данные

Выведите одно число — время в пути, усредненное по всем возможным временам начала (т.е. среднее арифметические времен в пути, вычисленных для всех возможных целочисленных времен старта от t ₁ до t ₂ включительно). Ваш ответ будет считаться верным, если его относительная погрешность будет не более 10 ^- 9 . Это обозначает, что, если ваш ответ равен a , а правильный — b , то должно выполняться | a - b | ≤ 10 ^- 9 b .

Примечание

В примере король может выехать в любой момент между 6 и 9 включительно.

Если король выезжает в момент времени 6, то к первому светофору он подъезжает в момент времени 10, этот светофор еще горит зеленым, поэтому король едет дальше без остановки. Ко второму светофору король подъезжает в момент времени 14, этот светофор в этот момент загорается красным, поэтому король ждет до момента времени 15, когда светофор загорается опять зеленым. Итого получается время в пути равно 9.

Если король выезжает в момент времени 7, то к первому светофору он подъезжает в момент времени 11, когда этот светофор только загорелся красным — король ждет до момента времени 12. Ко второму светофору король подъезжает в момент времени 16, когда этот светофор уже горит зеленым. Итого получается время в пути равно 9.

Если король выезжает в момент времени 8 или 9, то он не ждет ни на одном светофоре, и время в пути получается 8.

Итого среднее время в пути есть (9 + 9 + 8 + 8) / 4 = 8.5 .

Примеры

Входные данные

Выходные данные

8.5000000000

Страница: << 3 4 5 6 7 8 9 Отображать по:

Выбрано

Отменить

Добавить в контест