Темы --> Информатика --> Алгоритмы --> Вычислительная геометрия
    Градиентный спуск(1 задач)
    Элементарная геометрия(144 задач)
    Многоугольники. Выпуклые оболочки(38 задач)
    Клеточная геометрия(8 задач)
    Квадродерево(3 задач)
---> 4 задач <---
Источники --> Личные олимпиады --> Нижегородская олимпиада школьников
    2009(6 задач)
    2010(6 задач)
    2011(6 задач)
    2012(6 задач)
    2013(6 задач)
    XI Нижегородская городская олимпиада по информатике им. В. Д. Лелюха, 2015г.(6 задач)
    XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г.(6 задач)
Страница: 1 Отображать по:
#3881
Пересечение
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Компания, производящая оборудование для сотовой связи, обратилась к вам с просьбой написать программу, оценивающую качество организации сети. Одним из важных параметров является то, пересекаются ли зоны покрытия передатчиков, работающих на одинаковых частотах. Для простоты будем считать, что область покрытия каждого передатчика представляет собой многоугольник на плоскости (не обязательно выпуклый). Две области покрытия будем считать пересекающимися, если у них есть хотя бы одна общая точка (возможно, лежащая на границе одной или даже обеих областей). Ваша программа должна принимать на вход набор пар многоугольников, описывающих зоны покрытия передатчиков, и выводить про каждую пару информацию о том, пересекаются ли эти зоны.

Входные данные

На первой строке входного файла находится число \(K\) — количество тестов во входном файле. Далее идёт описание \(K\) тестов. Каждый тест задаётся описанием двух многоугольников, которые надо проверить на пересечение. Каждый многоугольник задаётся в следующем формате: сначала указывается одно число \(N_i\) — число вершин этого многоугольника, после чего идут \(N_i\) строк, каждая из которых содержит два разделённых пробелом числа \(x_{ij}\) и \(y_{ij}\) — координаты \(j\)-й вершины этого многоугольника. Вершины перечислены в порядке обхода многоугольника.

Число пар многоугольников в одном тесте \(1 \leq K \leq 10\), число вершин каждого многоугольника \(3 \leq N_i \leq 100\), координаты вершин — целые числа, \(|x_{ij}|, |y_{ij}| \leq 10\,000\).

Выходные данные

Для каждой пары многоугольников выведите в выходной файл на отдельной строке одно слово: “YES”, если многоугольники пересекаются, и “NO”, если нет.

Примеры
Входные данные
2
3
0 0
-1 0
0 -1
3
1 1
2 1
1 2
4
0 0
2 0
2 2
0 2
4
1 1
3 1
3 3
1 3
Выходные данные
NO
YES
#3887
Метро
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

В городе N строят метро. Вася, житель города N, хочет знать, сколько станций окажутся недалеко от его дома. Помогите ему.

Город N отличается очень строгой планировкой улиц: каждая улица идёт либо строго с юга на север, либо строго с востока на запад; при этом расстояние между соседними параллельными улицами одинаково. Соответственно, в городе есть много перекрёстков, расположенных в вершинах квадратной сетки. По планам, первая линия метро будет прямой и будет иметь станции на каждом перекрёстке, через который она пройдёт. Вася считает, что станция находится недалеко от его дома, если расстояние по прямой от его дома до станции не превосходит некоторой фиксированной величины \(R\).

Входные данные

Введём систему координат с осью \(x\), направленной с востока на запад, и осью \(y\), направленной с юга на север, с началом координат на одном из перекрёстков и с единицей длины, равной расстоянию между соседними параллельными улицами. Таким образом, улицы будут прямыми с уравнениями ..., \(x=-2\), \(x=-1\), \(x=0\), \(x=1\), \(x=2\), ..., а также ..., \(y=-2\), \(y=-1\), \(y=0\), \(y=1\), \(y=2\), ...

Во первой строке входного файла находятся целые числа \(x_0\), \(y_0\) — координаты Васиного дома (считаем, что он находится на некотором перекрёстке), — и расстояние \(R\) в тех же единицах измерения, в которых введены координаты. Во второй строке находятся четыре числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты некоторых двух различных перекрёстков, через которые пройдёт линия метро. Все координаты во входном файле не превосходят \(100\,000\,000\) по модулю; расстояние \(R\) целое, положительное и не превосходит \(100\,000\,000\).

Можете считать, что линия метро будет бесконечной в обоих направлениях.

Выходные данные

В выходной файл выведите одно число — количество станций, расположенных недалеко от Васиного дома.

Примечание

Первый пример соответствует рисунку; на рисунке дом Васи и станции метро обозначены жирными точками.

Примеры
Входные данные
2 2 3
0 -1 1 1
Выходные данные
2
Входные данные
0 0 1
-5 0 -3 0
Выходные данные
3
#3894
Освещение двора
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Фирма, в которой всё ещё работает ваш друг, собирается расширяться на новые маршруты, и потому приобрела новую площадку для ночного отстоя автобусов. Площадка раньше относилась к военной части, поэтому она имеет необычную форму — форму треугольника, огороженного забором.

Для того, чтобы освещать площадку ночью, на ней надо установить несколько прожекторов. К счастью, у фирмы как раз в наличие есть три регулируемых прожектора, а на территории площадки обнаружились три высоких столба. Было решено на каждый столб повесить по прожектору и отрегулировать их так, чтобы каждый прожектор освещал ровно одну из трёх сторон забора: один прожектор должен освещать одну сторону забора, другой — другую, третий — третью. Никакой прожектор не должен освещать ни миллиметра “чужой” стены.

Конечно, прожекторы должны освещать не только забор, но вообще всю территорию площадки, поэтому возникла проблема: надо определить, какой прожектор на какую сторону забора направить. Зная ваши высокие навыки в решении подобных задач, фирма обратилась к вам за помощью. Напишите программу, которая будет решать эту задачу.

Естественно, каждый прожектор освещает не только стену, но и всю соответствующую часть двора — треугольник с вершиной в месте, где находится столб, на котором висит прожектор, и основанием, совпадающим с соответствующей стороной забора. Будем считать, что стороны этого треугольника тоже освещены прожектором. Тенью от столбов пренебрегайте.

Входные данные

Первая строка входного файла содержит одно число \(T\) — количество тестовых примеров, которые идут дальше (\(1\leq T\leq 1000\)).

Далее следуют описания \(T\) примеров. В каждом сначала идут шесть чисел \(x_1\), \(y_1\), \(x_2\), \(y_2\), \(x_3\), \(y_3\) — координаты вершин площадки, после чего идут шесть чисел \(X_1\), \(Y_1\), \(X_2\), \(Y_2\), \(X_3\), \(Y_3\) — координаты столбов. Гарантируется, что все столбы находятся строго внутри площадки. Гарантируется, что площадь площадки строго больше нуля. Гарантируется, что никакие два столба не совпадают. Все координаты во входном файле целые и не превосходят по модулю \(800\).

Выходные данные

Выведите в выходной файл \(T\) строк по три числа в каждой: для каждого примера выведите номер стороны забора, на которую должен светить прожектор, находящийся на первом столбе, потом номер стороны, на которую должен светить прожектор со второго столба, и наконец номер стороны, на которую должен светить прожектор с третьего столба.

Первая сторона — та, которая соединяет вершины \((x_1, y_1)\) и \((x_2, y_2)\), вторая — \((x_2, y_2)\) и \((x_3, y_3)\), третья — \((x_3, y_3)\) и \((x_1, y_1)\).

Если решения не существует, выведите в соответствующую строку выходного файла три минус единицы: “-1 -1 -1”.

Примечание

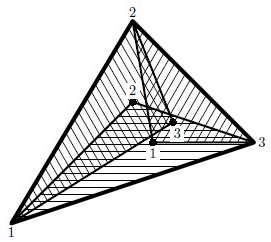
Первый пример соответствует рисунку.

Среди тестов будут такие, в которых \(T\leq 10\); суммарная стоимость таких тестов будет 70 баллов.

Примеры
Входные данные
2
0 0 6 10 12 4
7 4 6 6 8 5
-10 -10 0 10 10 -10
0 1 0 -1 1 1
Выходные данные
2 3 1
3 2 1
#111500
Дуга, отрезок и точка
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

На плоскости заданы дуга окружности, отрезок и точка. Как отрезок, так и дуга окружности непрозрачны. Определите, какая часть дуги видна из этой точки.

Входные данные

Входной файл состоит из трёх строк, описывающих данные объекты. Первая строка описывает дугу и содержит пять чисел — координаты центра дуги, радиус дуги, полярный угол точки начала дуги и полярный угол точки конца дуги. Полярные углы заданы в градусах и отсчитываются относительно центра дуги против часовой стрелки от положительного направления оси \(x\). Вторая строка описывает точку и содержит два числа — её координаты. Третья строка описывает отрезок и содержит четыре числа — координаты начала и конца отрезка. Все числа во входном файле вещественны и не превосходят \(10^6\) по модулю. Гарантируется, что как радиус окружности, так и длина отрезка больше нуля, что полярный угол конца дуги больше, чем полярный угол начала, и что разность этих углов не превосходит 360.

Гарантируются, что никакие два из данных трёх объектов не имеют общих точек.

Выходные данные

Выведите в выходной файл одно число на отрезке от 0 до 1 — относительную часть дуги, которая видна из данной точки. Ваш ответ должен отличаться от правильного не более, чем на 10−4.

Примечание
Система оценивания:
  • Группа тестов 1 (40 баллов). В этой группе во всех тестах дуга либо полностью видна, либо полностью не видна.
  • Группа тестов 2 (60 баллов). Нет ограничений. Только при прохождении группы 1.
Примеры
Входные данные
2 1 2 120 420
3 6
2 4 2.5 4
Выходные данные
0.496842552858631315
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест