В фирме, в которой работает ваш друг, ввели новый дизайн билетов на маршрутки. Теперь номер билета может быть любым натуральным числом. Радостные пассажиры тут же придумали новый, очень простой способ определения счастливости номера билета. Он состоит в следующем. Пусть номер билета равен \(N\). Если \(N<10\), то счастливость числа \(N\) (т.е. и самого билета) равна \(N\), иначе: посчитаем сумму цифр числа \(N\), пусть она равна \(S\) — тогда счастливость числа \(N\) будет равна счастливости числа \(S\).
Например, счастливость билета с номером \(7351\) равна счастливости билета с номером \(16\) (т.к. \(7+3+5+1=16\)), а она в свою очередь равна счастливости билета с номером 7 (т.к. \(1+6=7\)), а последняя просто равна 7 (т.к. \(7<10\)).
Такое определение счастливости вполне устроило обычных пассажиров маршрутки, но совсем не устроило большинство студентов, которые быстро нашли способ без особенных усилий определять счастливость билета. Поэтому, используя это определение, они придумали новую игру: обладатель билета должен разложить его номер в сумму нескольких чисел так, чтобы суммарная счастливость слагаемых была максимальна.
Но и эта игра устроила не всех студентов. Наиболее активные из них заметили, что игра становится ещё более интересной, если раскладывать \(N\) не в сумму, а в произведение чисел, с целью, по-прежнему, максимизировать сумму счастливостей множителей.
Напишите программу, которая будет решать эту задачу, т.е. по данному \(N\) находить такое его представление \(N=a_1\cdot a_2\cdot \ldots\), где все \(a_i\) натуральны, больше единицы, и суммарная счастливость чисел \(a_1\), \(a_2\), ... максимальна.
Для вашего удобства номер билета \(N\) задан его разложением на простые множители. Таким образом, первая строка входного файла содержит одно натуральное число — количество множителей в разложении числа \(N\) на простые, а далее следуют сами множители. \(N\) не превосходит \(10^{18}\), а каждый простой множитель не превосходит \(10^9\).
Если оптимальных решений несколько, выведите любое.
В выходной файл выведите искомое разложение \(N\) на множители. А именно, сначала выведите количество множителей в вашем разложении, а потом — сами множители.
Если ваша программа будет проходить тесты, в которых \(N\leq 10^9\), то она получит не менее 30 баллов.
3 2 2 3
2 6 2
2 2 11
2 2 11
Большое количество соревнований по разным видам спорта проводится по так называемой “олимпийской системе”. В простейшем варианте она состоит в следующем. В турнире участвуют \(N=2k\) игроков. Они получают номера от 1 до \(N\), и в первом круге игрок 1 играет с игроком 2, игрок 3 — с игроком 4 и т.д., игрок (\(N−1\)) — с игроком \(N\). Проигравшие в каждой паре выбывают из соревнований, а победители проходят во второй круг. Там победитель первой пары (т.е. игрок 1 или игрок 2) играет с победителем второй пары и т.д. Таким образом, в первом круге участвуют \(N=2k\) игроков, во втором круге — N2=2k−1 и т.д., в последнем круге (финале) участвуют два игрока.
Серьёзной проблемой при организации соревнований по олимпийской системе является то, что некоторые сильные игроки могут встретиться между собой уже в одном из первых кругов, в результате чего некоторые сильные участники могут рано выбыть из борьбы, в то время как другие, менее сильные участники могут пройти намного выше, если им повезёт с соперниками. Для борьбы с этим эффектом применяется так называемый “рассев” игроков, когда начальная нумерация участников не является полностью случайной, и вероятность “везения”/“невезения” с соперниками резко уменьшается.
В этой задаче вам нужно будет написать программу, находящую в некотором смысле оптимальный “рассев” игроков. Для этого рассмотрим следующую модель.
Предположим, что участников можно упорядочить по силе так, что более сильный игрок всегда будет выигрывать у более слабого. В таком случае по изначальному “рассеву” игроков дальнейший ход соревнований будет однозначно определён. Тогда в качестве критерия оптимальности “рассева” можно потребовать выполнение следующих условий:
* в финале играют двое сильнейших игроков,
* в полуфиналах играют четверо сильнейших игроков,
* и т.д.: в каждом круге играют только сильнейшие игроки (т.е. если в каком-то круге n мест, то в этом круге должны участвовать n сильнейших игроков).
Вам дано \(N\). Найдите хотя бы один оптимальный рассев.
Входной файл содержит одно число \(N\) — количество участников соревнований. Гарантируется, что \(N\) будет степенью двойки и что \(1\leq N\leq 2^{17}\).
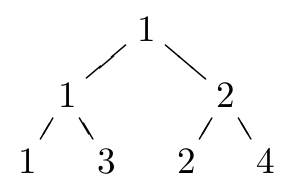
Занумеруем игроков по их силе от 1 до \(N\) (1 — наиболее сильный, \(N\) — наименее). Выведите в выходной файл оптимальный “рассев” участников, т.е. выведите \(N\) чисел, \(i\)"=ое из которых будет номером игрока, который должен стоять на \(i\)"=м месте в оптимальном “рассеве”.
Если существует несколько оптимальных “рассевов”, выведите любой. Если оптимального “рассева” не существует, выведите в выходной файл одно число \(-1\).
4
1 3 2 4
В последнее время в одной из школ Н. Новгорода, а также на одном из факультетов ННГУ стала очень популярна игра в настольный теннис. Игроки часто сталкиваются со следующей проблемой: довольно трудно уследить за всем ходом матча и при этом не сбиться со счёта, поэтому очень хотелось бы иметь программу, подсчитывающую счёт. Напишите программу, которая по данному протоколу матча восстановит итоговый счёт.
Протокол состоит из последовательности следующих событий: service, net, out, goal, return, eom.
События обозначают следующее:
* service — подача (при этом игрок ударяет по мячу). service — всегда первое событие во входном файле. После него могут следовать net, out, goal, return.
* net — мяч ударяется о половину поля того игрока, который ударял по мячу последним, слишком много раз. Игрок, который ударял по мячу последним, проигрывает розыгрыш. После этого события могут идти service или eom.
* out — мяч уходит в аут. Игрок, который ударял по мячу последним, проигрывает розыгрыш. После этого события могут идти service или eom.
* goal — игрок, который ударял по мячу последним, забивает гол (т.,е. выигрывает розыгрыш). Далее может быть service или eom.
* return — игрок отбивает мяч, ударяя по нему (игроки ударяют по мячу по очереди). Далее может быть net, out, goal, return.
* eom — матч окончен. Это всегда последнее событие.

Когда игрок выигрывает розыгрыш, ему начисляется очко. Когда игрок проигрывает розыгрыш, очко начисляется его противнику.
Подачи подаются по пять штук, т.,е. первые пять подач подаёт первый игрок, следующие пять — другой и т.д. Полное количество подач может быть не кратным пяти, в таком случае последняя серия подач будет короче пяти штук.
Конечно, в реальном матче может произойти ситуация, которую невозможно описать этими событиями, но ваша программа должна считать, что весь матч описывается данными во входном файле событиями.
Во входном файле находится список событий. События расположены по одному на строке без пробелов. Последовательность событий удовлетворяет всему, что было сказано выше; пустых строк во входном файле нет (кроме, возможно, строк после события eom). Всего событий не более 50000.
В выходной файл выведите два числа: очки того, кто подавал первым, потом — очки его противника.
service goal service out service net service return return return out service return goal service goal eom
2 4
service out eom
0 1
На плоскости заданы дуга окружности, отрезок и точка. Как отрезок, так и дуга окружности непрозрачны. Определите, какая часть дуги видна из этой точки.
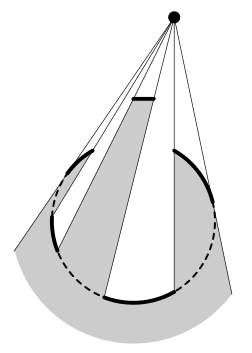
Входной файл состоит из трёх строк, описывающих данные объекты. Первая строка описывает дугу и содержит пять чисел — координаты центра дуги, радиус дуги, полярный угол точки начала дуги и полярный угол точки конца дуги. Полярные углы заданы в градусах
и отсчитываются относительно центра дуги против часовой стрелки от положительного направления оси \(x\). Вторая строка описывает точку и содержит два числа — её координаты. Третья строка описывает отрезок и содержит четыре числа — координаты
начала и конца отрезка. Все числа во входном файле вещественны и не превосходят \(10^6\) по модулю. Гарантируется, что как радиус окружности, так и длина отрезка больше нуля, что полярный угол конца дуги больше, чем полярный угол начала, и
что разность этих углов не превосходит 360.
Гарантируются, что никакие два из данных трёх объектов не имеют общих точек.
Выведите в выходной файл одно число на отрезке от 0 до 1 — относительную часть дуги, которая видна из данной точки. Ваш ответ должен отличаться от правильного не более, чем на 10−4.
- Группа тестов 1 (40 баллов). В этой группе во всех тестах дуга либо полностью видна, либо полностью не видна.
- Группа тестов 2 (60 баллов). Нет ограничений. Только при прохождении группы 1.
2 1 2 120 420 3 6 2 4 2.5 4
0.496842552858631315
На зачёте по квантовым вычислениям преподаватель решил сделать всё возможное, чтобы избежать списывания. За время семестра он успел выделить несколько пар студентов, которые, по его мнению, могут списывать друг у друга, при этом каждый студент входит не более чем в одну такую пару. Теперь преподаватель хочет придумать такую рассадку для студентов, чтобы они все решали задачи самостоятельно.
Зачёт проводится в аудитории, в которой стоит один большой круглый стол, за которым ровно \(N\) мест; студентов в группе тоже ровно \(N\). Преподаватель считает, что списывать сложнее всего, если тот, у кого списывают, находится на расстоянии ровно \(L\) от того, кто списывает. Таким образом, преподаватель хочет рассадить студентов так, чтобы между каждыми двумя студентами, которые могут списывать друг у друга, сидело бы ровно \(L\)−1 других студентов.
Помогите преподавателю найти такую рассадку.
Примечание Ясно, что в зависимости от того, с какого именно из двух студентов начинать считать, и в зависимости от того, в какую сторону считать, получится разное количество человек, сидящих между ними. Преподавателю требуется лишь, чтобы для каждой пары, начиная с хотя бы какого-нибудь из этих двух студентов, хотя бы в какую-нибудь сторону до другого студента насчитывался бы ровно \(L\)−1 студент.
Первая строка входного файла содержит три числа: \(N\), \(L\) и \(K\), где \(N\) — количество студентов в группе, \(L\) — оптимальное “антисписывательное” расстояние, а \(K\) — количество пар студентов, которые могут друг у друга списывать. Далее следуют \(K\) строк по два числа в каждой — номера студентов, входящих в очередную пару. Студенты нумеруются от 1 до \(N\). Все числа во входном файле натуральные и не превосходят 8000; гарантируется, что \(L\) < \(N\).
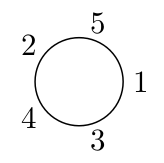
Если искомая рассадка существует, то выведите в выходной файл любой из возможных ответов, т.е. \(N\) чисел — номера студентов в порядке обходе стола против часовой стрелки начиная с любого места. Если решения не существует, выведите −1.
5 3 2 1 4 2 3
1 5 2 4 3