В городе N строят метро. Вася, житель города N, хочет знать, сколько станций окажутся недалеко от его дома. Помогите ему.
Город N отличается очень строгой планировкой улиц: каждая улица идёт либо строго с юга на север, либо строго с востока на запад; при этом расстояние между соседними параллельными улицами одинаково. Соответственно, в городе есть много перекрёстков, расположенных в вершинах квадратной сетки. По планам, первая линия метро будет прямой и будет иметь станции на каждом перекрёстке, через который она пройдёт. Вася считает, что станция находится недалеко от его дома, если расстояние по прямой от его дома до станции не превосходит некоторой фиксированной величины \(R\).
Введём систему координат с осью \(x\), направленной с востока на запад, и осью \(y\), направленной с юга на север, с началом координат на одном из перекрёстков и с единицей длины, равной расстоянию между соседними параллельными улицами. Таким образом, улицы будут прямыми с уравнениями ..., \(x=-2\), \(x=-1\), \(x=0\), \(x=1\), \(x=2\), ..., а также ..., \(y=-2\), \(y=-1\), \(y=0\), \(y=1\), \(y=2\), ...
Во первой строке входного файла находятся целые числа \(x_0\), \(y_0\) — координаты Васиного дома (считаем, что он находится на некотором перекрёстке), — и расстояние \(R\) в тех же единицах измерения, в которых введены координаты. Во второй строке находятся четыре числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты некоторых двух различных перекрёстков, через которые пройдёт линия метро. Все координаты во входном файле не превосходят \(100\,000\,000\) по модулю; расстояние \(R\) целое, положительное и не превосходит \(100\,000\,000\).
Можете считать, что линия метро будет бесконечной в обоих направлениях.
В выходной файл выведите одно число — количество станций, расположенных недалеко от Васиного дома.
Первый пример соответствует рисунку; на рисунке дом Васи и станции метро обозначены жирными
точками.
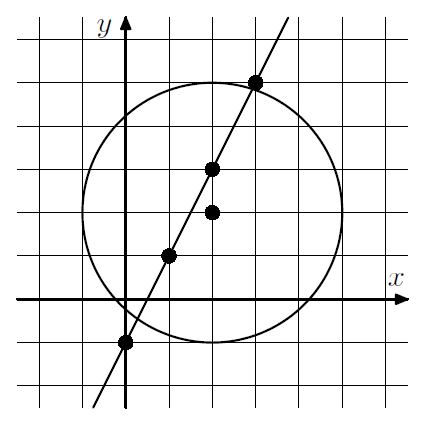
2 2 3 0 -1 1 1
2
0 0 1 -5 0 -3 0
3
Фирма, в которой всё ещё работает ваш друг, решила установить в своих маршрутках автоматы по продаже чая и кофе, чтобы во время поездок и, особенно, во время ожидания в пробках, пассажиры могли с толком провести время.
Стоимость стакана чая и кофе в автомате предполагается установить равной пяти рублям. Автоматы будут принимать монеты по 5 и 10 рублей, а также купюры в 10, 50 и 100 рублей. Когда пассажиру надо выдавать сдачу (т.е. когда пассажир бросил в автомат десятирублёвую монету или 10-, 50- или 100-рублёвую купюру), автомат выдаёт сдачу пятирублёвыми монетами; если же пассажир бросил в автомат пятирублёвую монету, то автомат её сохраняет и может использовать для сдачи следующим пассажирам.
Ясно, что, чтобы обеспечить возможность выдачи сдачи всем покупателям, может потребоваться изначально загрузить в автомат некоторое количество пятирублёвых монет. Сейчас на маршрутках фирмы проходят испытания с целью определить минимальное количество монет, которые надо загрузить в автомат перед выездом маршрутки в рейс. Вам дан протокол одного из таких испытаний: известен порядок, в котором пассажиры оплачивали свои покупки различными монетами и купюрами. Определите, какое минимальное количество пятирублёвых монет должно было изначально находиться в автомате, чтобы всем пассажирам хватило сдачи.
В первой строке входного файла находится одно натуральное число \(N\) — количество покупок в автомате, которые были совершены в ходе испытания (\(1\leq N\leq 50\,000\)). Во второй строке находятся \(N\) натуральных чисел, каждое из которых равно номиналу монеты или купюры, которую использовал очередной покупатель для оплаты; каждый номинал может принимать одно из четырёх значений: 5, 10, 50 или 100.
В выходной файл выведите одно число — минимальное количество пятирублёвых монет, которые надо было загрузить в автомат изначально, чтобы всем покупателям хватило сдачи.
В первом примере одна пятирублёвая монета потребуется для сдачи первому покупателю и 19 монет — третьему, но при сдаче третьему можно будет использовать ту монету, которую бросит второй покупатель, поэтому изначально в автомате достаточно 19 монет.
Во втором примере сдачу третьему покупателю можно выдать, используя монету первого или второго покупателя, и поэтому не требуется загружать монеты в автомат изначально.
В третьем примере первому же покупателю требуются девять монет сдачи, и все они должны изначально находится в автомате.
3 10 5 100
19
3 5 5 10
0
4 50 5 5 5
9
Рассмотрим два числа \(a\) и \(b\). По ним можно однозначно определить такое целое \(k\), что \(\) b^k\leq a< b^{k+1}; \(\) это \(k\) мы будем называть целой частью логарифма \(a\) по основанию \(b\).
Напишите программу, которая будет вычислять целую часть логарифма.
В первой строке входного файла записано одно целое число \(a\) (\(1\leq a \leq 10^{100}\)) без ведущих нулей. Во второй строке входного файла записано целое число \(b\) (\(2\leq b\leq 100\)).
В выходной файл выведите одно число — целую часть логарифма \(a\) по основанию \(b\) без ведущих нулей.
12345678987654321 3
33
8 2
3
2 5
0
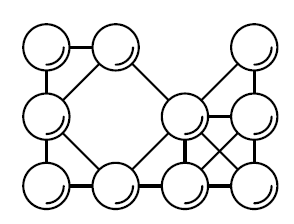Фирма, в которой работает ваш друг, решила установить на конечной остановке своих маршруток
большую абстрактную скульптуру со своим логотипом. Скульптура будет представлять собой
прямоугольную сетку из \(N\) строк и \(M\) столбцов, в некоторых узлах которой будут располагаться разноцветные шары.
Для обеспечения жёсткости конструкции шары, расположенные в узлах, соседних по вертикали,
горизонтали или диагонали, необходимо соединить металлическими стержнями. Более строго, два шара
должны быть соединены стержнем, если разность номеров строк, в которых расположены эти шары, не
превосходит по модулю единицы, и разность номеров столбцов тоже не превосходит по модулю единицы.
Напишите программу, которая по заданному расположению шаров позволит определить, как будет выглядеть скульптура после установки стержней.
В первой строке входного файла находятся два натуральных числа \(N\) и \(M\) — размеры конструкции (\(1\leq
N,M\leq 100\)). Далее следуют \(N\) строк по \(M\) символов в каждой. Каждый символ — это или
“#” (решетка), обозначающий, что в соответствующем узле будет находиться шарик, или “.” (точка),
обозначающий, что соответствующий узел будет пустой.
Выведите в выходной файл \(2N-1\) строку по \(2M-1\) символов в каждой,
изображающие как сами шары, так и соединяющие их стержни. А именно,
в нечётных позициях нечётных строк выведите символ “#”
или “.”, в зависимости от того, заполнен этот узел шариком или нет,
а в остальных позициях выведите один из символов “ ” (пробел),
“-” (минус), “|” (вертикальная
палочка, ASCII #124),
“/” (дробь, ASCII #47), “\” (обратный слеш, ASCII #92) или “X”
(латинская заглавная буква X, ASCII #88), отражающий конфигурацию стержней в соответствующем месте структуры.
Если какая-то строка выходного файла должна заканчиваться на пробелы, их можно не выводить.
Первый пример соответствует рисунку.
3 4 ##.# #.## ####
#-# . # |/ \ /| # . #-# |\ /|X| #-#-#-#
3 4 .#.. #.#. .#..
. # . . / \ # . # . \ / . # . .
В секретном 240 отделе ИПФ РАН \(N\) сотрудников и \(N\) компьютеров. В отделе вводятся новые требования к секретности. В соответствии с этими требованиями, для каждого сотрудника будут определены ровно \(K\) компьютеров, к которым этот сотрудник будет иметь допуск (т.е. за которыми этот сотрудник будет иметь право работать), причём так, что к каждому компьютеру будут иметь допуск ровно \(K\) сотрудников.
Информация о том, какой сотрудник к какому компьютеру будет иметь допуск, будет известна лишь непосредственно перед вступлением новых требований в силу. Таким образом, чтобы не прерывать работу отдела, сотрудники должны будут быстро решить, кто за каким компьютером будет работать. Для этого им необходимо заранее написать программу, которая по любому распределению допусков сотрудников найдёт рассадку сотрудников по компьютерам, удовлетворяющую этим допускам.
Обратите внимание, что значение \(K\) тоже будет известно лишь в последний момент. Из общих соображений секретности известно лишь, что \(K\) будет равняться или 1, или 2, или 4; поэтому ваша программа должна уметь работать для любого из этих трех значений \(K\).
В первой строке входного файла записаны натуральные числа \(N\) и \(K\) (\(1\leq N \leq 500\)). Далее следуют \(KN\) строк, в каждой из которых записаны два натуральных числа — номер сотрудника и номер компьютера, к которому этот сотрудник имеет допуск.
Гарантируется, что каждый сотрудник имеет допуск ровно к \(K\) компьютерам, что к каждому компьютеру ровно \(K\) сотрудников имеют допуск, и что \(K\) равно либо 1, либо 2, либо 4.
В выходной файл выведите \(N\) строк, в каждой по два числа — номер сотрудника и номер компьютера, за которым он должен работать. Строки можно выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Можно доказать, что для любого входного файла, удовлетворяющего указанным ограничениям, всегда имеется как минимум одно решение.
3 1 2 3 3 1 1 2
3 1 1 2 2 3
2 2 1 2 2 1 2 2 1 1
1 2 2 1