Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 544 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 11 12 13 14 15 16 17 >> Отображать по:
#714
Турнир
  
За победу команда получает 2 очка, за ничью - 1, за поражение - 0. По известным результатам команд требуется восстановить турнирную таблицу.

В турнире по хоккею участвовало K команд, каждая сыграла с каждой по одному матчу. За победу команда получала 2 очка, за ничью – 1, за поражение – 0 очков.

Известно, сколько очков в итоге получила каждая команда, однако результаты конкретных матчей были утеряны. Требуется восстановить одну из возможных турнирных таблиц.

Входные данные

В первой строке входных данных содержится одно натурально число K, не превосходящее 100 – количество команд. Во второй строке  задаются  через пробел K целых неотрицательных чисел, не превосходящих 2(K–1), – количество очков, набранных командами, занявшими первое, второе, …, K-е места соответственно (то есть каждое следующее число не больше предыдущего).

Выходные данные

Выведите турнирную таблицу в следующем формате. Таблица должна состоять из K строк с результатами игр команд, занявших первое, второе, …, последнее место (команды, набравшие одинаковое число очков, могут быть расположены в таблице в любом порядке). В каждой строке должно быть записано K чисел через пробел – количество очков, набранных в игре данной команды с первой, второй, … командами соответственно. Количество очков – это число 0, 1 или 2. В клетках на главной диагонали (соответствующих не существующей игре команды "самой с собой") нужно записать нули.

Гарантируется, что входные данные соответствуют реальному турниру, то есть хотя бы одна таблица, соответствующая входным данным, может быть построена. Если таких таблиц несколько, выведите любую из них.

Примеры
Входные данные
4
6 4 2 0
Выходные данные
0 2 2 2 
0 0 2 2
0 0 0 2
0 0 0 0
Входные данные
4
3 3 3 3
Выходные данные
0 2 0 1
0 0 2 1
2 0 0 1
1 1 1 0
#715
Морской бой
  
Заданы начальные координаты и скорости кораблей на плоскости. Есть бомбы, уничтожающие корабли на расстоянии не превышающем R от центра взрыва. Взрывать бомбы можно только в целые моменты времени. Требуется уничтожить все корабли наименьшим количеством бомб.

N вражеских кораблей движутся прямолинейно с постоянными скоростями. Вакуумная бомба уничтожает все объекты в радиусе R от точки взрыва (то есть все объекты, расстояние от которых до точки взрыва не больше R). Взрывать бомбу можно только в целые моменты времени.

Требуется определить, за какое наименьшее количество взрывов можно уничтожить все корабли, а также в какие моменты времени и в каких точках для этого следует произвести взрывы. Время отсчитывается от момента, когда координаты движущихся кораблей были определены со спутника.

Входные данные

В первой строке входных данных задаются целые числа N (2 <= N <= 10) и R (0 < R ≤ 50. В следующих Nстроках  содержится по 4 числа, описывающих движение кораблей. Первые два числа строки – координаты корабля в момент времени 0, по модулю не превосходящие 105. Следующие два числа – значения координат вектора скорости, по модулю не превосходящие 1000. Все эти числа целые.

Гарантируется, что никакие 2 корабля не имеют одинаковые векторы скорости.Однако вполне возможно, что в какой-то момент времени два корабля пройдут через одну точку.

Выходные данные

В первой строке выведите одно число – минимальное количество взрывов K. В следующих K строках для каждого взрыва выведите по три числа: целое время взрыва и вещественные координаты взрыва, указанные с точностью не менее трех значащих цифр после точки. Разрешается производить взрывы как в разные, так и в один и тот же момент времени. Разрешается взрывы производить как в различных точках, так и в одной точке в разные моменты времени.

Если решений несколько, выведите любое из них.

Комментарий. Решения, верно работающие при N ≤ 3, будут набирать не менее 50 баллов.

Примеры
Входные данные
3 3
-3 3 1 0
0 -6 0 2
-8 6 4 -1
Выходные данные
1
3 2.000 1.500
Входные данные
2 1
-4 -4 2 2
2 2 -2 -2
Выходные данные
2
0 -4.0000 -4.0000
0 2.0000 2.0000
#720
Минимальное число
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Дано натуральное четырехзначное число. Найдите минимальное натуральное четырехзначное число, состоящее из тех же цифр, что и заданное. Заметим, что четырехзначные числа не могут начинаться с нуля.

Входные данные

Вводится натуральное четырехзначное число.

Выходные данные

Выведите минимальное натуральное  четырехзначное число, состоящее из тех же цифр.

Примеры
Входные данные
1513
Выходные данные
1135
#721
Шнурки
  
Темы: [Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N.

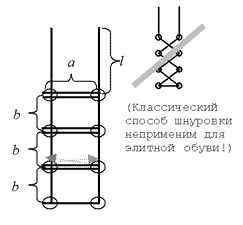Рис. 1 Шнуровка должна происходить элитным способом «наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.» (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l.

Какова должна быть длина шнурка для этих ботинок?

Входные данные

Вводятся четыре натуральных числа a, b, l и N.

Выходные данные

Ваша программа должна выводить одно число – искомую длину шнурка.

Примеры
Входные данные
2 1 3 4
Выходные данные
26
#722
Пересадки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На Новом проспекте для разгрузки было решено пустить два новых автобусных маршрута на разных участках проспекта.  Известны конечные остановки каждого из автобусов. Определите количество остановок, на  которых можно пересесть с одного автобуса на другой.

Входные данные

Вводятся четыре числа, не превосходящие 100, задающие номера конечных остановок. Сначала для первого, потом второго автобуса (см. примеры и рисунок).

Выходные данные

Ваша программа должна выводить одно число – искомое количество остановок.

 Задача В, рис. 2

Пояснения

Первый пример (см. рисунок): первый автобус ходит с 3-й остановки по 6-ю и обратно, а второй с 2-й по 4-ю и обратно. Пересесть с одного автобуса на другой можно на 3-й и 4-й остановках. Их две.

Второй пример: автобусы не имеют общих остановок.

Примеры
Входные данные
3 6 4 2
Выходные данные
2
Входные данные
3 1 5 10
Выходные данные
0
Страница: << 11 12 13 14 15 16 17 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест