Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 74 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#497
Автобусы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В столице одной Очень Демократической Страны все жители в 8 часов утра одновременно выходят со станций метро, ближайших к месту своей работы, и дальше добираются до работы на автобусах. Мэр города хочет построить еще одну станцию метро так, чтобы после этого время, к которому все люди доберутся до места своей работы (то есть время, когда последний работник окажется на работе), было наименьшим возможным.

Автобусное сообщение в столице устроено следующим образом. Есть N автобусных остановок, в частности, возле каждой станции метро расположено по остановке. Между N – 1 парой остановок постоянно курсируют автобусы, время движения от одной остановки до другой – 1 минута. Временем ожидания и пересадки можно пренебречь. Автобусное сообщение в столице организовано так, что от любой автобусной остановки до любой другой можно добраться на автобусах (возможно, с пересадками).

Входные данные

В первой строке входных данных содержатся два числа N и M – количество автобусных остановок и станций метро соответственно (2 ≤ N ≤ 50 000, 1 ≤ M ≤ 1 000, M < N).

Во второй строке задаются через пробел M чисел – номера автобусных остановок, рядом с которыми есть станции метро (каждая – не более одного раза).

В следующих N – 1 строках записано по два числа – номера автобусных остановок, между которыми курсирует автобус. (Автобус ходит в обоих направлениях. Каждый маршрут указан один раз.)

Выходные данные

Выведите два числа – сначала наибольшее время за которое кто-то будет и после строительства добираться на работу, а затем номер автобусной остановки, рядом с которой следует построить новую станцию метро. (Строить можно возле тех автобусных остановок, возле которых еще нет станций метро). Если решений несколько, выведите одно из них.

Подзадачи и система оценки

Данная задача содержит две подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1 (40 баллов)

В этой подзадаче \(N \leq 2000\)

Подзадача 2 (60 баллов)

Дополнительные ограничения отсутствуют.

Примеры
Входные данные
8 2
1 2
1 2
1 3
1 4
2 5
2 6
6 7
6 8
Выходные данные
1
6
Входные данные
8 2
5 3
1 2
1 3
1 4
2 5
2 6
6 7
6 8
Выходные данные
2
6
#510
Метро
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Задано описание метрополитена в виде описания веток. Каждая ветка содержит номера станций, которые на ней находятся. Станция, присутствующая на нескольких ветках - пересадочная. Требуется определить маршрут от станции до станции с минимальным количеством пересадок.

Метрополитен состоит из нескольких линий метро. Все станции метро в городе пронумерованы натуральными числами от 1 до \(N\). На каждой линии расположено несколько станций. Если одна и та же станция расположена сразу на нескольких линиях, то она является станцией пересадки и на этой станции можно пересесть с любой линии, которая через нее проходит, на любую другую (опять же проходящую через нее).

Напишите программу, которая по данному вам описанию метрополитена определит, с каким минимальным числом пересадок можно добраться со станции \(A\) на станцию \(B\). Если данный метрополитен не соединяет все линии в одну систему, то может так получиться, что со станции \(A\) на станцию \(B\) добраться невозможно, в этом случае ваша программа должна это определить.

Входные данные

Сначала вводится число \(N\) — количество станций метро в городе (2≤\(N\)≤100). Далее следует число \(M\) — количество линий метро (1≤\(M\)≤20). Далее идет описание \(M\) линий. Описание каждой линии состоит из числа \(P_i\) — количество станций на этой линии (2≤\(P_i\)≤50) и \(P_i\) чисел, задающих номера станций, через которые проходит линия (ни через какую станцию линия не проходит дважды).

Затем вводятся два различных числа: \(A\) — номер начальной станции, и \(B\) — номер станции, на которую нам нужно попасть. При этом если через станцию \(A\) проходит несколько линий, то мы можем спуститься на любую из них. Так же если через станцию \(B\) проходит несколько линий, то нам не важно, по какой линии мы приедем.

Выходные данные

Выведите минимальное количество пересадок, которое нам понадобится. Если добраться со станции \(A\) на станцию \(B\) невозможно, программа должна вывести одно число –1 (минус один).

Примеры
Входные данные
5
2
4 1 2 3 4
2 5 3
3 1
Выходные данные
0
Входные данные
5
5
2 1 2
2 1 3
2 2 3
2 3 4
2 4 5
1 5
Выходные данные
2
Входные данные
10
2
6 1 3 5 7 4 9
6 2 4 6 8 10 7
3 8
Выходные данные
1
Входные данные
4
2
2 1 2
2 3 4
1 3
Выходные данные
-1
#556
Мехико
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
16 megabytes

Город Мехико расположен в прекрасной долине, известной как Долина Мехико, на месте которой много лет назад было озеро. Около 1300 года ацтекские религиозные лидеры выпустили указ о том, что центр озера должен быть засыпан, чтобы построить столицу их империи. В настоящее время озеро полностью осушено.

Вокруг озера до появления ацтеков были расположены c прибрежных городов. Некоторые из этих городов заключили между собой коммерческие соглашения. Между городами, установившими коммерческие соглашения, по озеру на лодках перевозились различные товары. Любую пару городов можно было соединить отрезком прямой, полностью проходящим через озеро.

В какой-то момент короли городов решили упорядочить товароперевозки. Они разработали маршрут товароперевозок, который соединяет все города вокруг озера. Маршрут удовлетворяет следующим условиям:

*Он начинается в каком-либо городе, проходит через каждый прибрежный город и заканчивается в городе, отличном от того, в котором он начался.
*Маршрут проходит через каждый город ровно один раз.
*Любые два последовательно посещаемых города маршрута обязаны иметь между собой коммерческое соглашение.
*Маршрут состоит из отрезков прямых, каждый из которых соединяет два последовательно посещаемых города маршрута.
*Чтобы избежать столкновения лодок, маршрут не должен иметь самопересечений.


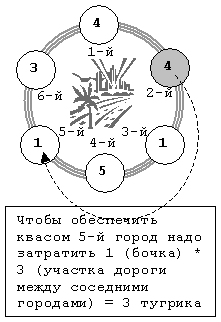
На рисунке показано озеро и города вокруг него. Тонкие и жирные линии отрезков обозначают коммерческие соглашения между городами. Жирные линии показывают маршрут грузоперевозок, начинающийся в городе 2 и заканчивающийся в городе 5.

Этот маршрут нигде не имеет самопересечений. Но если построить маршрут, идущий из города 2 в город 6, затем в город 5, а затем в город 1, то он будет неправильным, поскольку имеет самопересечения.

Города нумеруются целыми числами от 1 до \(c\) по направлению часовой стрелки.

Задание

Напишите программу, которая по заданному числу городов \(c\) и списку коммерческих соглашений между городами, найдет маршрут товароперевозок, удовлетворяющий указанным выше условиям.

Ограничения

3 ≤ \(c\) ≤ 1000, \(c\) – число городов вокруг озера

Входные данные

На вход Вашей программы поступают данные в следующем формате:

СТРОКА 1: Содержит целое число \(c\).
СТРОКА 2: Содержит целое число \(n\) – количество коммерческих соглашений.
СЛЕДУЮЩИЕ \(n\) СТРОК: Каждая строка описывает одно коммерческое соглашение (одно соглашение описывается один раз). В строке задаются два целых числа, разделенных пробелами, которые соответствуют номерам городов, заключивших между собой коммерческое соглашение.

Выходные данные

Если возможно построить маршрут товароперевозок, выведите c строк, в каждой из которых записано целое число. Эти числа представляют собой порядок посещения городов по маршруту товароперевозок. Если невозможно построить маршрут товароперевозок, удовлетворяющий всем указанным требованиям, выведите одну строку, содержащую отрицательное целое число -1.

Замечание

Если существует несколько маршрутов товароперевозок, удовлетворяющих всем указанным требованиям, выведите любой из них.

Оценивание

Ряд тестов с общей суммой 30 баллов будет удовлетворять следующим ограничениям:
3 ≤ \(m\) ≤ 10
3 ≤ \(n\) ≤ 10

Примеры
Входные данные
7
9
1 4
5 1
1 7
5 6
2 3
3 4
2 6
4 6
6 7
Выходные данные
5
6
7
1
4
3
2
#608
Витрина
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Зал супермаркета имеет форму прямоугольника размером \(M\) x \(N\), в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.

В супермаркет привезли новую супервитрину размером \(K\) x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.

Входные данные

В первой строке вводятся три натуральных числа \(M\), \(N\) и \(K\) (\(M\), \(N\) ≤ 100, \(K\) ≤ \(M\)). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число \(V\) – количество витрин (0 ≤ \(V\) ≤ \(N\)*\(M\)). В следующих \(V\) строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до \(M\)–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до \(N\)–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.

Выходные данные

В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:

U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать \(N\) x \(M\).

Если возможных маршрутов несколько, то выведите любой из них.

Примеры
Входные данные
10 10 5
0
Выходные данные
0
RUURUURUURUURU
Входные данные
9 3 2
4
2 0
5 1
5 2
8 2
Выходные данные
1
URRRDRRRRUU
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест