#1312

Последовательность

Темы: [Быстрая сортировка]

Источники: [ Личные олимпиады, Украинские олимпиады, 2000, 1 день, Задача A ]

Дана последовательность, состоящая из 2N натуральных чисел. Известно, что все числа этой последовательности можно разбить на пары таким образом, что сумма чисел во всех парах будет одинаковой. Например, числа последовательности 99, 23, 77, 1 можно разбить на пары 1+99=77+23.

Напишите программу, которая по такой последовательности определяет, можно ли эту последовательность разбить на пары таким образом, чтобы произведение чисел во всех парах было одинаковым.

Входные данные

Файл содержит данные нескольких тестов. Первая строка содержит натуральное число - количество тестов в файле. Первая строка каждого теста содержит число 2N — количество чисел в последовательности. В каждой из последующих 2N строчек содержится целое число от 1 до 10⁹— элементы последовательности (1≤N≤ 50000)

Выходные данные

Файл должен содержать ответ на каждый из тестов в отдельной строке. Ответом на тест является символ 1, если входную последовательность можно разбить на пары, произведения в которых были бы одинаковыми, и 0 в противном случае.

Примеры

Входные данные

Выходные данные

0
1

#1338

НГУ-стройка

Темы: [Быстрая сортировка] [Сканирующая прямая]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2009, Задача B ]

Заданы параллелепипеды с целочисленными координатами. Необходимо выбрать минимальный набор параллелепипедов, покрывающих горизонтальный слой.

Над ареной огромного спортивного комплекса Независимого Главного Университета (НГУ) решили построить перекрытие. Перекрытие будет построено по клеевой технологии и состоять из склеенных друг с другом блоков. Блок представляет собой легкий прямоугольный параллелепипед. Два блока можно склеить, если они соприкасаются перекрывающимися частями боковых граней ненулевой площади.

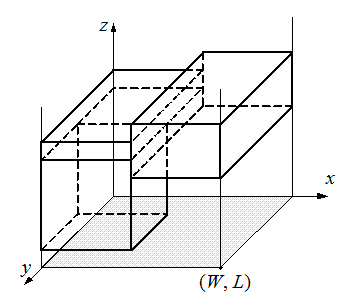
НГУ представил план комплекса, имеющий вид прямоугольника размером W на L. При этом один из углов прямоугольника находится в начале системы координат, а другой имеет координаты (W, L). Стены комплекса параллельны осям координат.

Подрядчики известили НГУ, что они готовы к определенному сроку изготовить блоки и установить их. Для каждого блока фиксировано место его возможного монтажа, совпадающее по размерам с этим блоком. Места выбраны так, что ребра блоков параллельны осям координат. Места монтажа блоков не пересекаются.

По техническим условиям перекрытие должно состоять из такого набора склеенных блоков, который содержит сплошной горизонтальный слой ненулевой толщины. Торопясь ввести комплекс в эксплуатацию, НГУ решил построить перекрытие из минимально возможного числа блоков.

Требуется написать программу, которая позволяет выбрать минимальное число блоков, которые, будучи установленными на указанных подрядчиками местах, образуют перекрытие, либо определить, что этого сделать невозможно. Высота, на которой образуется перекрытие, не имеет значения.

Входные данные

В первой строке входного файла указаны три целых числа: N — количество возможных блоков (1 ≤ N ≤ 10⁵) и размеры комплекса W и L (1 ≤ W, L ≤ 10⁴). Каждая из последующих N строк описывает место монтажа одного блока, определяемое координатами противоположных углов: (x₁, y₁, z₁) и (x₂, y₂, z₂), при этом 0 ≤ x₁ < x₂ ≤ W, 0 ≤ y₁ < y₂ ≤ L, 0 ≤ z₁ < z₂ ≤ 10⁹. Все числа во входном файле целые и разделяются пробелами или переводами строк.

Гарантируется, что места установки блоков не пересекаются друг с другом.

Выходные данные

Первая строка выходного файла должна содержать либо слово «YES», если перекрытие возможно построить, иначе — слово «NO». В первом случае вторая строка выходного файла должна содержать минимальное число блоков, образующих перекрытие, а последующие строки — номера этих блоков, в соответствии с порядком, в котором они перечислены во входном файле.

Если возможно несколько минимальных наборов блоков, выведите любой из них.

Примечания

Решения, корректно работающие в случае, когда все числа во входном файле не превышают 100, будут оцениваться из 40 баллов.

Примеры

Входные данные

1 10 10
0 0 0 10 10 10

Выходные данные

YES
1
1

Входные данные

2 10 10
0 0 0 10 5 5
0 5 5 10 10 10

Выходные данные

NO

#1341

Граффити на заборе

Темы: [Бинарный поиск по ответу] [Быстрая сортировка] [Жадный алгоритм]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2009, Задача E ]

Около прямолинейного забора, состоящего из N одинаковых бетонных плит, проводится конкурс граффити, в котором участвуют M граффити-художников. Художники должны разрисовать все плиты своими произведениями за наименьшее возможное время.

Плиты пронумерованы числами от 1 до N, граффити-художники имеют номера от 1 до M. Первоначально i-й граффити-художник находится около плиты с заданным номером p_i. Каждому художнику требуется b минут на разрисовывание любой плиты. Каждую плиту должен разрисовать ровно один граффити-художник.

В начале работы, а также после разрисовывания любой плиты граффити-художник может перейти к любой неразрисованной плите. Время перемещения граффити-художника от любой плиты к соседней с ней одинаково и равно a минут. Таким образом, чтобы перейти от плиты с номером i к плите с номером j художнику требуется a×|i – j| минут.

Требуется написать программу, которая поможет участникам конкурса разрисовать все плиты за минимальное возможное время.

Входные данные

В первой строке входного файла указаны числа N — количество плит в заборе и M — количество граффити-художников (1 ≤ N, M ≤ 100000). Во второй строке заданы два целых числа: a — количество минут, которое требуется для перехода от любой плиты к соседней, и b — количество минут, которое требуется граффити-художнику на разрисовывание одной плиты (1 ≤ a, b ≤ 10⁶). В третьей строке заданы M чисел p₁, p₂, …, p_M — начальные положения граффити-художников (1 ≤ p_i ≤ N).

Выходные данные

В первую строку выходного файла выведите минимальное количество минут, требуемых художникам для выполнения работы.

В последующих M строках выведите описание действий художников. В i-й из этих строк должно содержаться описание действий i-го художника: количество плит, которые должен разрисовать этот художник, и номера этих плит в очередности их разрисовывания. Если оптимальных решений несколько, можно вывести любое из них.

Примечание

Решения, корректно работающие при M ≤ 2, будут оцениваться из 40 баллов.

Примеры

Входные данные

10 2
19 56
9 2

Выходные данные

375
5 10 9 8 7 6 
5 1 2 3 4 5

#1344

Многоугольники

Темы: [Быстрая сортировка] [Элементарная геометрия]

Источники: [ Личные олимпиады, Украинские олимпиады, 2002, 2 день, Задача B ]

На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:

никакие два многоугольника не имеют общих точек;
для каждого i –го многоугольника существует P_i многоугольников, внутри которых он находится, и N-1-P_i многоугольников, которые находятся внутри его, 0 ≤P_i≤N-1.

Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.

Входные данные

Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число C_i — количество вершин многоугольника, 3≤C_i≤20. Последующие C_i пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.

Выходные данные

Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть P_i — количество многоугольников, внутри которых находится i–ый многоугольник.

Примеры

Входные данные

3
3 -2 1 8 9 12 1
3 7 5 6 3 7 4
4 4 3 7 7 9 3 1 2

Выходные данные

0 2 1

#1387

Предпраздничная суета

Темы: [Сортировка подсчетом] [Бинарный поиск по ответу] [Быстрая сортировка]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2008-2009, Заключительный этап, Задача C ]

Помимо открыток Петя и Вася решили устроить одноклассницам чаепитие и заразили своей идеей еще K–2 своих друзей. Они собрались вместе и выбрали в одном довольно известном супермаркете P тортиков. Настал черед рассчитываться за них.

В магазине есть N работающих касс, занумерованных числами от 1 до N. Про i-ю кассу известно, что кассиру требуется A_i единиц времени на обработку одного товара и B_i единиц времени для того, чтобы рассчитаться с покупателем. Обойдя все кассы, школьники посчитали, что на обслуживание покупателей, уже стоящих в i-ю кассу, уйдет T_i единиц времени.

Теперь Петя и Вася задались вопросом, в какие кассы надо встать им и их друзьям (в каждую из выбранных касс должен стоять хотя бы один из них, и каждый из них может стоять не более, чем в одну кассу, поэтому суммарно они могут стоять не более чем в K касс) и сколько тортиков каждый должен взять, чтобы последний из них вышел из магазина как можно раньше. Некоторые из ребят могут в кассу не стоять, а, отдав все тортики другим, выйти через специальный выход для тех, кто ничего не купил.

Напишите программу, которая определит это минимальное время.

Входные данные

В первой строке записано одно число N — количество касс в супермаркете (1 ≤ N ≤ 100000). В следующих N строках записано по три числа A_i, B_i, T_i(0 ≤ A_i, B_i, T_i ≤ 100000). В последней строке записаны два числа — K и P — число школьников и покупок у них соответственно (0 ≤ P ≤ 100000, 2 ≤ K ≤ 100000).

Все числа во входном файле целые.

Выходные данные

Выведите минимальное время выхода последнего школьника из магазина.

Комментарии к примерам тестов

Здесь лучше всего встать в обе кассы и купить там по одному тортику.

Выгоднее всего одному из школьников встать со всеми тортиками в первую кассу, а остальным выйти без покупок.

Частичные ограничения

Первая группа состоит из тестов, в которых N ≤ 10 и оценивается в 30 баллов.

Вторая группа состоит из тестов, в которых N ≤ K ≤ 100000 и оценивается в 30 баллов.

Третья группа состоит из тестов без дополнительного ограничения и оценивается в 40 баллов.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные