Темы --> Информатика --> Структуры данных --> Деревья
    Куча(30 задач)
    Двоичное дерево поиска(24 задач)
    Дерево отрезков, RSQ, RMQ(90 задач)
    Бор(14 задач)
    Дерево Фенвика(6 задач)
    Декартово дерево(10 задач)
---> 43 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 3 4 5 6 7 8 9 >> Отображать по:
#113251
Подчисло
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Петрик и Василько — настоящие друзья, поэтому они постоянно задают друг другу всевозможные интересные задачи. Однако Василько всегда с легкостью решает задачи своего друга, поэтому Петрик решил придумать по-настоящему сложную задачу. И вот что у него получилось. Будем называть число b подчислом числа a , если из числа a можно вычеркнуть некоторые цифры так, что цифры, которые остались, образуют число b . Задано n -цифровое число x . Обозначим как x k наибольшее k -цифровое подчисло числа x . Необходимо ответить на m запросов. Каждый запрос состоит из двух цифр - k и l . Ответом на запрос является l -я цифра числа x k . На этот раз задача действительно заставила Василько задуматься. А сможете ли вы решить ее быстрее его?

Входные данные

В первой строке входного файла содержится целое число x длины n ( 1 ≤ n ≤ 100 000 ). Во второй строке содержится число m ( 1 ≤ m ≤ 50 000 ). В следующих m строках содержится по два числа k i , l i ( 1 ≤ k i ≤ n , 1 ≤ l i ≤ k i ) — параметры i -го запроса.

Выходные данные

Выходной файл должен содержать одну строку длины m , i -й символ которого является ответом на i -й запрос.

Примечание

  1. n = 20, m = 10 000 .( 15 баллов)
  2. n · m ≤ 500 000 .( 25 баллов)
  3. n ≤ 100 000, m ≤ 50 000 .( 60 баллов)
Примеры
Входные данные
31415926
7
2 2
3 1
1 1
4 3
5 2
8 2
7 3
Выходные данные
6992511
#113539
Продажа картин
  
Источники: [ Личные олимпиады, COCI, COCI 2015-2016, Раунд 1, Продажа картин ]
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
32 megabytes

Лука - торговец картинами. У него есть N клиентов, каждому из которых он продает произведения искусства. Каждый клиент может купить либо цветные картины, либо черно-белые, но не те и другие вместе. При этом клиент под номером i готов купить не более a i цветных картин и не более b i черно-белых картин. При этом каждый клиент хочет купить хотя бы одну картину.

У Луки практически неограниченный запас картин, поэтому запросы клиентов не являются для него проблемой. Однако, Лука не любит продавать черно-белые картины, и если окажется, что меньше, чем C людей купили цветные картины, он очень огорчится.

В силу нестабильной экономической ситуации в стране клиенты постоянно изменяют свои запросы, иными словами количество цветных и черно-белых картин, которые они готовы купить. Из-за этого Лука постоянно задается вопросом: "Сколько у меня есть вариантов, как продать клиентам картины, чтобы хотя бы C человек купили цветные картины?". Помогите Луке и защитите его от излишнего беспокойства.

Входные данные

Первая строка содержит два целых числа N и C ( 1 ≤ N ≤ 105, 1 ≤ C ≤ 20 ). Вторая строка содержит N целых чисел a i ( 1 ≤ a i ≤ 109 ). Третья строка содержит N целых чисел b i ( 1 ≤ b i ≤ 109 ). Четвертая строка содержит одно целое число Q ( 1 ≤ Q ≤ 105 ) - количество изменений требований клиентов. Каждая из следующих Q строк содержит три числа: номер клиента, меняющего требования P ( 1 ≤ P ≤ N ), новое максимальное количество цветных картин, которое он готов купить A p ( 1 ≤ A p ≤ 109 ) и новое максимальное количество черно-белых картин, которое он готов купить B p ( 1 ≤ B p ≤ 109 ).

Выходные данные

Выведите Q строк, где в q -й строке записано единственное число - количество вариантов продать картины клиентам, чтобы хотя бы C человек купили цветные картины, по модулю 10007 после первых q изменений требований.

Разбалловка для личной олимпиады

Тесты 4-6 — числа n, q не превосходят 1000. Группа тестов оценивается в 30 баллов.

Тесты 7-13 — Полные ограничения. Группа тестов оценивается в 70 баллов.

Примеры
Входные данные
2 2
1 1
1 1
1
1 1 1
Выходные данные
1
Входные данные
2 2
1 2
2 3
2
1 2 2
2 2 2
Выходные данные
4
4
Входные данные
4 2
1 2 3 4
1 2 3 4
1
4 1 1
Выходные данные
66
#113540
Игра Мирко
  
Источники: [ Личные олимпиады, COCI, COCI 2015-2016, Раунд 1, Игра Мирко ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Мирко большой любитель шахмат и программирования, но обычные шахматы уже наскучили ему, поэтому он начал экспериментировать и придумал свою игру. Он взял шахматную доску с N рядами и N столбцами и расположил на ней K ладей. Игра Мирко следует таким правилам: 1. У каждой ладьи есть своя сила, заданная натуральным числом. 2. Ладья видит все клетки поля в своем ряду и своем столбце кроме той, на которой стоит сама. 3. Клетка считается атакованной в том случае, если побитовый XOR сил всех ладей, которые видят эту клетку, положителен. Изначально Мирко некоторым образом расположил ладьи на поле, и теперь собирается сделать P перемещений. Каждый раз он будет брать одну ладью и ставить ее на другую клетку поля (при этом ладья не обязательно будет перемещена вдоль ряда или столбца в котором она стоит). После каждого перемещения, определите сколько клеток на поле атакованы.

Входные данные

Первая строка содержит 3 целых числа N , K , P ( 1 ≤ N ≤ 1000000000 , 1 ≤ K , P ≤ 10000 ). Каждая из следующих K строк содержит 3 натуральных числа R i , C i , X i ( 1 ≤ R i , C i ≤ N , 1 ≤ X i ≤ 1000000000 ), которые обозначают что на клетке ( R i , C i ) стоит ладья с силой X i . Каждая из следующих P строк содержит 4 натуральных числа R 1 , C 1 , R 2 , C 2 ( 1 ≤ R 1, C 1, R 2, C 2 ≤ N ), которые означают что ладья, стоящая на клетке ( R 1, C 1 ), была передвинута на поле ( R 2, C 2 ). Гарантируется, что в момент перемещения на клетке ( R 1, C 1 ) есть ладья и что ни в какой момент времени на одной клетке нет двух и более ладей.

Выходные данные

Выведите P строк, где в k -й строке записано единственное число - количество клеток поля, атакованных после первых k перемещений.

Примеры
Входные данные
2 2 2
1 1 1
2 2 1
2 2 2 1
1 1 1 2
Выходные данные
4
0
Входные данные
2 2 2
1 1 1
2 2 2
2 2 2 1
1 1 1 2
Выходные данные
4
2
Входные данные
3 3 4
1 1 1
2 2 2
2 3 3
2 3 3 3
3 3 3 1
1 1 1 2
3 1 3 2
Выходные данные
6
7
7
9
#113545
Иллюзия сортировки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Известный программист пробует себя в роли иллюзиониста. Его коронный фокус состоит в следующем.

Для заданного массива из n целых неотрицательных чисел a1, a2, ..., an он быстро подбирает магическое число b. Целое неотрицательное число b называется магическим для массива, если применение операции побитового исключающего ИЛИ с этим числом к каждому элементу массива превращает его в отсортированный массив. Иначе говоря,

\(\) (a_1\oplus b) \le (a_2\oplus b) \le ... \le (a_n\oplus b) \(\)

где \(\oplus\) — операция побитового исключающего ИЛИ.

Чтобы фокус был более эффектным, после предъявления магического числа для заданного массива иллюзионист q раз выполняет следующее действие. Он предлагает зрителям изменить один из элементов массива и после этого снова пытается предъявить магическое число. При этом программист настолько отточил свое мастерство иллюзиониста, что каждый раз предъявляет зрителям минимальное возможное магическое число. Иногда фокус не удаётся, так как для полученного массива невозможно подобрать магическое число.

Требуется написать программу, которая по заданному исходно массиву, а также после каждого изменения элемента, вычисляет минимальное магическое число для полученного массива, либо определяет, что такого числа нет.

Примечание

Исключающее ИЛИ — это логическая операция, обозначаемая знаком \(\oplus\), которая задаётся следующей таблицей истинности:

Определим побитовое исключающее ИЛИ для двух неотрицательных целых чисел x и y. Запишем каждое из целых чисел x и y в двоичной системе счисления, дополнив при необходимости более короткое из чисел ведущими нулями до равной длины. Побитовое исключающее ИЛИ двух целых чисел \(x\) и \(y\), обозначаемое также как \(\oplus\), это целое неотрицательное число, каждый разряд которого в двоичной системе счисления является исключающим ИЛИ соответствующих разрядов чисел \(x\) и \(y\). Например, \(5\oplus22=101_2\oplus10110_2=10011_2=19\).

Среди предложенных на олимпиаде языков программирования в языке Паскаль для обозначения исключающего ИЛИ используется оператор «xor», в остальных языках программирования используется оператор «^».

Входные данные

Первая строка входных данных содержит целое число n — количество чисел в массиве (1 ≤ n ≤ 106).

Вторая строка содержит n целых чисел a1, a2, ..., an — элементы массива (0 ≤ ai < 230).

Третья строка содержит целое число q — число изменений элемента массива (0 ≤ q ≤ 106).

Следующие q строк содержат по два целых числа pi и vi, где pi — номер элемента массива, который следует заменить (1 ≤ pi ≤ n), а vi — новое значение этого элемента (0 ≤ vi < 230).

Выходные данные

Выходные данные должны содержать (q + 1) целых чисел b0, b1, ..., bq, по одному в строке.

Значение b0 — либо минимальное возможное магическое число для исходного массива, либо  - 1, если такого числа не существует.

Для i от 1 до q значение bi — либо минимальное возможное магическое число для массива после первых i изменений, либо  - 1, если такого числа не существует.

Примеры
Входные данные
3
0 1 4
3
2 7
3 3
1 4
Выходные данные
0
2
-1
4
#113550
Антивещество
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

Компания тестирует технологию получения антивещества, используемого в качестве топлива в межпланетном звездолёте. Антивещество получается в результате специальных экспериментов в реакторе.

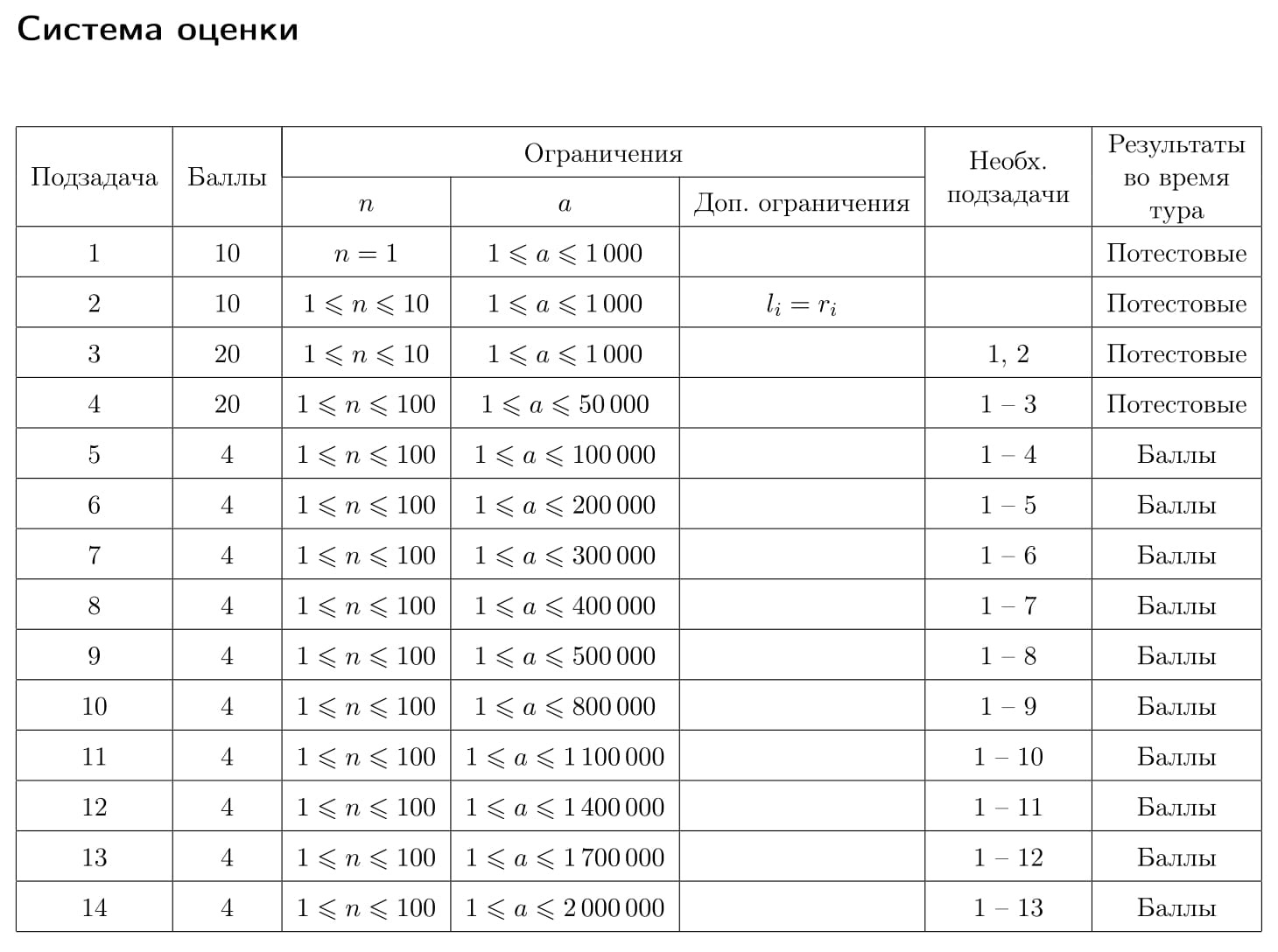
Известно n типов экспериментов, приводящих к получению антивещества. В результате проведения эксперимента i-го типа в выходной контейнер реактора добавляется от li до ri граммов антивещества. Из соображений безопасности запрещается накапливать в контейнере более a граммов антивещества.

Затраты на проведение эксперимента i-го типа составляют ci, а стоимость одного грамма полученного антивещества составляет 109.

Если после проведения экспериментов в контейнере образовалось t граммов антивещества, а суммарные затраты на проведение экспериментов в реакторе составили s, то прибыль определяется по формуле (t·109 - s). Компании необходимо разработать стратегию проведения экспериментов, позволяющую максимизировать прибыль, которую можно гарантированно получить.

В зависимости от результатов предыдущих экспериментов стратегия определяет, эксперимент какого типа следует провести, или решает прекратить дальнейшее выполнение экспериментов. Стратегия позволяет гарантированно получить прибыль x, если при любых результатах проведения экспериментов: во-первых, в контейнере реактора оказывается не более a граммов антивещества, во-вторых, прибыль составит не менее x.

Например, пусть возможен только один тип эксперимента, порождающий от 4 до 6 граммов антивещества, затраты на его проведение равны 10, а вместимость контейнера составляет 17 граммов. Тогда после двукратного проведения эксперимента в контейнере может оказаться от 8 до 12 граммов антивещества. Если получилось 12 граммов, то больше проводить эксперимент нельзя, так как в случае получения 6 граммов антивещества контейнер может переполниться. В остальных случаях можно провести эксперимент в третий раз и получить от 12 до 17 граммов антивещества. В худшем случае придётся провести эксперимент трижды, затратив в сумме 30, прибыль составит (12·109 - 30) = 11 999 999 970.

Требуется написать программу, которая определяет максимальную прибыль x, которую гарантированно можно получить.

Входные данные

Первая строка входных данных содержит два целых числа: n — количество типов экспериментов и a — максимально допустимое количество антивещества в контейнере (1 ≤ n ≤ 100, 1 ≤ a ≤ 2 000 000).

Следующие n строк содержат по три целых числа li, ri и ci — минимальное и максимальное количество антивещества, получаемое в результате эксперимента типа i, и затраты на эксперимент этого типа, соответственно (1 ≤ li ≤ ri ≤ a, 1 ≤ ci ≤ 100).

Выходные данные

Выходные данные должны содержать одно целое число — максимальную прибыль x, которую гарантированно можно получить.

Примеры
Входные данные
1 17
4 6 10
Выходные данные
11999999970
Входные данные
2 11
2 2 100
3 5 5
Выходные данные
9999999890
Страница: << 3 4 5 6 7 8 9 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест