Страница: 1 Отображать по:
#113548
Накопитель
  
Темы: [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Исследуется новое цифровое устройство для хранения информации. Информация на устройстве хранится в виде последовательности ячеек, каждая из которых находится в одном из двух состояний, обозначаемых символами «+» и «-», и, таким образом, хранит один бит информации.

Назовём фрагментом группу соседних ячеек с одинаковым состоянием, слева от которой либо нет ячеек, либо находится ячейка в противоположном состоянии, и справа — либо нет ячеек, либо находится ячейка в противоположном состоянии.

Операция записи позволяет выбрать любую пару соседних фрагментов разной длины и изменить состояние всех ячеек более короткого фрагмента на противоположное, объединяя таким образом два или три соседних фрагмента в один.

Требуется написать программу, которая по заданной исходной и итоговой последовательностям состояний ячеек определяет, можно ли из исходной последовательности получить итоговую с помощью последовательных операций записи.

Входные данные

Первая строка входных данных содержит целое положительное число q — количество тестов.

Каждая из следующих q строк содержит si, ti — непустые последовательности символов «+» и «-» одинаковой длины, разделённые одним пробелом. Эта строка означает, что в тесте номер i из исходной последовательности состояний ячеек si требуется получить итоговую последовательность ti.

Выходные данные

Выходные данные должны содержать q строк, где i-я строка равна «Yes», если из исходной последовательности состояний ячеек si можно получить итоговую последовательность ti, или «No» в противном случае.

Примеры
Входные данные
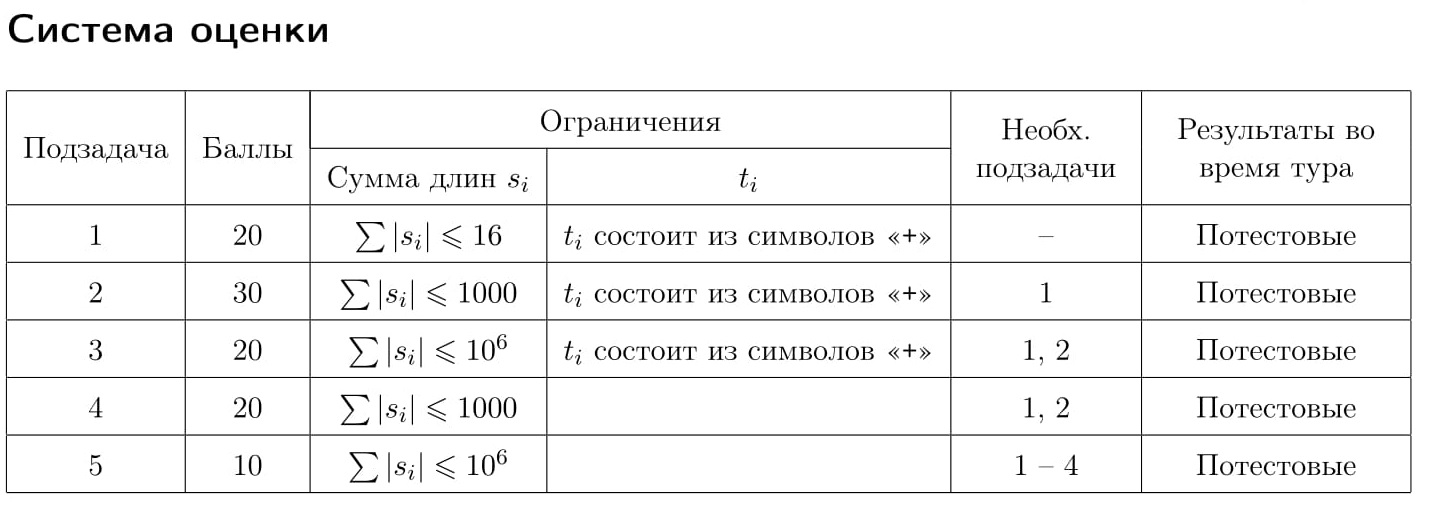
3
++- +++
++-- ++++
++-+--+- ++++++++
Выходные данные
Yes
No
Yes
Входные данные
3
++-+-- ++----
++-+-- +++---
-++- -++-
Выходные данные
Yes
No
Yes
#113549
Серверы на Меркурии
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
512 megabytes

Компьютерная система управления станциями на Меркурии состоит из n серверов, пронумерованных от 1 до n. Серверы соединены (n - 1) двусторонними каналами связи, i-й из которых соединяет i-й и (i + 1)-й серверы.

С Земли необходимо передать пакет обновления программного обеспечения для компьютерной системы управления. Пакет необходимо установить на каждый сервер. Стоимость передачи пакета обновления с Земли на Меркурий очень высока, поэтому с Земли пакет обновления передаётся только на один сервер. Затем пакет необходимо передать на все остальные серверы по каналам связи, возможно, через другие серверы.

Из-за высокой солнечной радиации на Меркурии передавать пакет обновления по каналам связи можно только в некоторые промежутки времени. Для i-го канала связи известен промежуток времени [li, ri], во время которого возможна передача пакета по этому каналу. Пакет передаётся по любому каналу связи мгновенно.

Пакет обновления, переданный на j-й сервер, немедленно устанавливается и помещается в специальный буфер памяти, из которого он может быть передан на другие серверы. Пакет находится в буфере памяти j-го сервера в течение tj секунд с момента его получения. Если в момент нахождения пакета в буфере памяти сервера появляется возможность передать его по каналу связи на соседний сервер, на котором пакет обновления пока не установлен, то он немедленно передаётся по этому каналу связи.

Поскольку пакет содержит важные обновления, требуется начать его распространение как можно раньше.

Требуется написать программу, которая для всех i от 1 до n определяет, возможно ли установить пакет обновления на все серверы, передав его с Земли на i-й сервер. Если это возможно, то необходимо определить, в какой минимальный неотрицательный момент времени можно установить пакет на этот сервер, чтобы в результате обновление оказалось установлено на всех серверах.

Входные данные

Первая строка входных данных содержит n — количество серверов (1 ≤ n ≤ 200 000).

Вторая строка содержит n целых чисел t1, t2, ..., tn, где tj — время нахождения пакета в буфере памяти j-го сервера (0 ≤ tj ≤ 109).

Следующие (n - 1) строк описывают каналы связи. Для описания i-го канала задаются два целых числа li и ri — границы промежутка времени, на протяжении которого возможна передача пакета по этому каналу (0 ≤ li ≤ ri ≤ 109).

Выходные данные

Выходные данные должны содержать n целых чисел a1, a2, ..., an.

Число ai должно быть равно такому минимальному неотрицательному моменту времени, что при установке пакета обновления на i-й сервер в момент ai, пакет будет в итоге установлен на всех серверах. Если такого момента времени для i-го сервера не существует, необходимо вывести ai =  - 1.

Примечание

В первом примере имеется всего один сервер, минимальное подходящее время, в которое можно установить на него обновление — 0.

Во втором примере есть два сервера, передать обновление между которыми можно в промежуток от 6 до 8. Первый сервер хранит обновление в буфере 3 единицы времени, а второй — 5 единиц времени. Если отправить обновление первому серверу в момент 3, то он передаст его второму серверу в момент 6. Аналогично если отправить обновление второму серверу в момент 1, то он передаст его первому серверу в момент 6.

В третьем примере нельзя передать обновление первому серверу так, чтобы оно передалось третьему серверу, так как канал 2–3 закрывается до того, как открывается канал 1–2. Можно отправить обновление второму или третьему серверу в момент 5. В этот момент канал 2–3 открыт, поэтому его сразу получат второй и третий серверы. В момент 7, когда откроется канал 1–2 обновление ещё будет находиться в буфере второго сервера, и передастся первому серверу.

В четвёртом примере второй сервер хранит пакет 0 единиц времени, а канал 2–3 открыт в промежуток 5–5. Чтобы передать обновление через второй сервер к третьему серверу, оно должно попасть ко второму серверу в момент 5. Если же мы хотим отправить обновление третьему серверу, то это можно сделать в момент 4, при этом оно будет храниться до момента 7 и будет в итоге установлено на все серверы.

Примеры
Входные данные
1
10
Выходные данные
0
Входные данные
2
3 5
6 8
Выходные данные
3
1
Входные данные
3
1 2 4
7 10
3 5
Выходные данные
-1
5
5
Входные данные
4
1 0 3 2
4 6
5 5
7 10
Выходные данные
5
5
4
-1
#113550
Антивещество
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

Компания тестирует технологию получения антивещества, используемого в качестве топлива в межпланетном звездолёте. Антивещество получается в результате специальных экспериментов в реакторе.

Известно n типов экспериментов, приводящих к получению антивещества. В результате проведения эксперимента i-го типа в выходной контейнер реактора добавляется от li до ri граммов антивещества. Из соображений безопасности запрещается накапливать в контейнере более a граммов антивещества.

Затраты на проведение эксперимента i-го типа составляют ci, а стоимость одного грамма полученного антивещества составляет 109.

Если после проведения экспериментов в контейнере образовалось t граммов антивещества, а суммарные затраты на проведение экспериментов в реакторе составили s, то прибыль определяется по формуле (t·109 - s). Компании необходимо разработать стратегию проведения экспериментов, позволяющую максимизировать прибыль, которую можно гарантированно получить.

В зависимости от результатов предыдущих экспериментов стратегия определяет, эксперимент какого типа следует провести, или решает прекратить дальнейшее выполнение экспериментов. Стратегия позволяет гарантированно получить прибыль x, если при любых результатах проведения экспериментов: во-первых, в контейнере реактора оказывается не более a граммов антивещества, во-вторых, прибыль составит не менее x.

Например, пусть возможен только один тип эксперимента, порождающий от 4 до 6 граммов антивещества, затраты на его проведение равны 10, а вместимость контейнера составляет 17 граммов. Тогда после двукратного проведения эксперимента в контейнере может оказаться от 8 до 12 граммов антивещества. Если получилось 12 граммов, то больше проводить эксперимент нельзя, так как в случае получения 6 граммов антивещества контейнер может переполниться. В остальных случаях можно провести эксперимент в третий раз и получить от 12 до 17 граммов антивещества. В худшем случае придётся провести эксперимент трижды, затратив в сумме 30, прибыль составит (12·109 - 30) = 11 999 999 970.

Требуется написать программу, которая определяет максимальную прибыль x, которую гарантированно можно получить.

Входные данные

Первая строка входных данных содержит два целых числа: n — количество типов экспериментов и a — максимально допустимое количество антивещества в контейнере (1 ≤ n ≤ 100, 1 ≤ a ≤ 2 000 000).

Следующие n строк содержат по три целых числа li, ri и ci — минимальное и максимальное количество антивещества, получаемое в результате эксперимента типа i, и затраты на эксперимент этого типа, соответственно (1 ≤ li ≤ ri ≤ a, 1 ≤ ci ≤ 100).

Выходные данные

Выходные данные должны содержать одно целое число — максимальную прибыль x, которую гарантированно можно получить.

Примеры
Входные данные
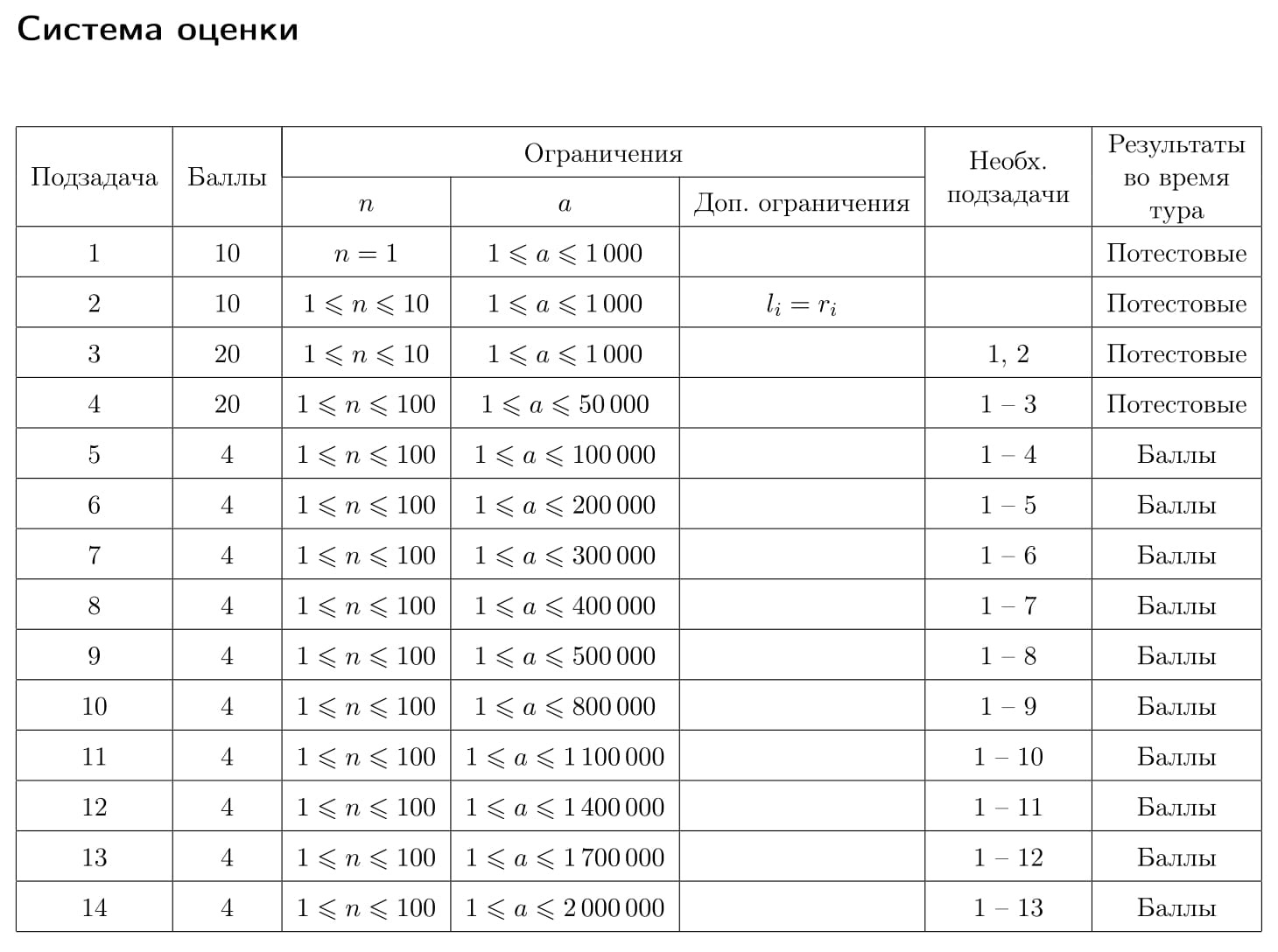
1 17
4 6 10
Выходные данные
11999999970
Входные данные
2 11
2 2 100
3 5 5
Выходные данные
9999999890
#113551
Траектория обучения
  
Темы: [Рекурсия] [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Победитель студенческой олимпиады получил предложения о стажировке от двух университетов. При подготовке планов обучения он узнал рейтинг качества преподавания каждой дисциплины в этих университетах.

Программа обучения первого университета состоит из последовательности перечисленных в хронологическом порядке n различных дисциплин a1, a2, ..., an, имеющих рейтинги x1, x2, ..., xn соответственно. Программа обучения второго университета состоит из последовательности перечисленных в хронологическом порядке m различных дисциплин b1, b2, ..., bm, имеющих рейтинги y1, y2, ..., ym соответственно.

Студент имеет возможность составить план обучения в первом университете таким образом, чтобы изучить дисциплины на позициях учебной программы с la по ra включительно (1 ≤ la ≤ ra ≤ n), либо отказаться от стажировки в первом университете. Аналогично он может составить план обучения во втором университете таким образом, чтобы изучить дисциплины на позициях учебной программы с lb по rb включительно (1 ≤ lb ≤ rb ≤ m), либо отказаться от стажировки во втором университете.

Изучать одну и ту же дисциплину дважды в разных университетах не имеет смысла, поэтому все дисциплины в двух выбранных планах обучения должны быть различны.

Требуется написать программу, которая определит планы обучения студента таким образом, чтобы получить наибольшую возможную сумму рейтингов изучаемых дисциплин.

Входные данные

Первая строка входных данных содержит целые числа n и m — количество дисциплин в программах обучения первого и второго университетов (1 ≤ n, m ≤ 500 000).

Вторая строка входных данных содержит n целых чисел ai — дисциплины, входящие в программу обучения первого университета, перечисленные в хронологическом порядке (1 ≤ ai ≤ n + m).

Третья строка входных данных содержит n целых чисел xi — рейтинги дисциплин, входящих в программу обучения первого университета, перечисленные том же порядке, что и дисциплины ai (1 ≤ xi ≤ 109).

Четвёртая строка входных данных содержит m целых чисел bi — дисциплины, входящие в программу обучения второго университета, перечисленные в хронологическом порядке (1 ≤ bi ≤ n + m).

Пятая строка входных данных содержит m целых чисел yi — рейтинги дисциплин, входящих в программу обучения второго университета, перечисленные том же порядке, что и дисциплины bi (1 ≤ yi ≤ 109).

Выходные данные

Первая строка выходных данных должна содержать целое число r — наибольшую возможную сумму рейтингов дисциплин.

Вторая строка выходных данных должна содержать целые числа la, ra — позиции в учебной программе первой и последней дисциплин, входящих в план обучения в первом университете, либо «0 0», если студент отказался от стажировки в первом университете.

Третья строка выходных данных должна содержать целые числа lb, rb — позиции в учебной программе первой и последней дисциплин, входящих в план обучения во втором университете, либо «0 0», если студент отказался от стажировки во втором университете.

Если возможных правильных ответов несколько, разрешается вывести любой из них.

Примечание

В первом тесте из условия приведённые планы обучения в университетах приводят к суммарному рейтингу дисциплин (7 + 4 + 10 + 1 + 5) + (5 + 3 + 4) = 27 + 12 = 39. Если бы студент выбрал только вторую и третью дисциплины в первом университете и весь курс обучения во втором университете, суммарный рейтинг дисциплин был бы (7 + 4) + (3 + 5 + 3 + 4 + 12) = 11 + 27 = 38.

Во втором тесте из условия первая и третья дисциплины во втором университете имеют настолько высокий рейтинг по сравнению с соответствующими дисциплинами первого университета, что наиболее выгодный вариант — пройти целиком стажировку во втором университете и отказаться от стажировки в первом университете.

Примеры
Входные данные
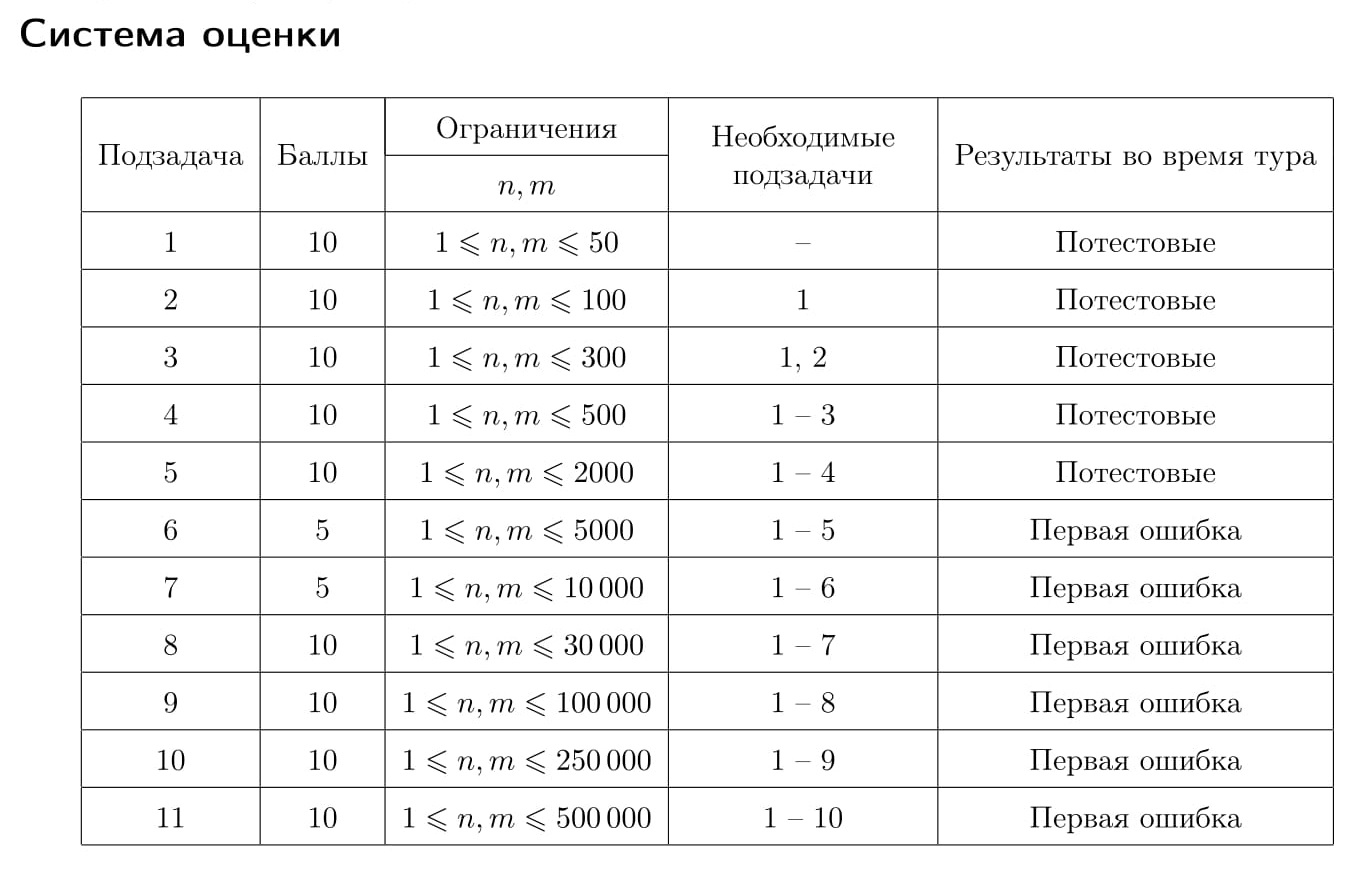
7 5
3 1 4 8 6 9 2
2 7 4 10 1 5 3
9 2 11 3 8
3 5 3 4 12
Выходные данные
39
2 6
2 4
Входные данные
2 3
1 2
1 4
2 3 1
17 2 15
Выходные данные
34
0 0
1 3
Входные данные
3 3
4 2 1
10 1 2
5 4 2
1 2 9
Выходные данные
19
1 1
3 3
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест