Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.
Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.
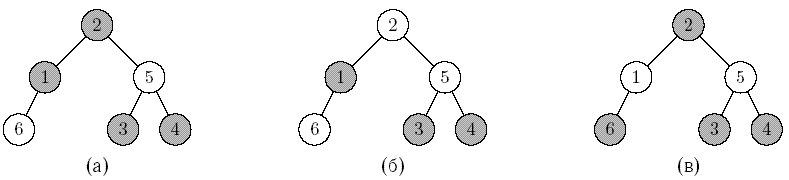 |
Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.
Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.
В первой строке вводится число n – количество вершин в дереве ( 1![]() n
n![]() 1000).
1000).
Пусть вершины дерева пронумерованы числами от 1 до n. Следующие n строк содержат по два числа – для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор вводимых чисел действительно задает двоичное дерево.
Выведите одно число – количество способов раскрасить вершины заданного двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.
 |
6 6 0 1 5 0 0 0 0 3 4 0 0
3
4 2 0 3 0 4 0 0 0
0
Максимальное время работы на одном тесте: 2 секунды
При разработке программ для просмотра веб-страниц одной из наиболее сложных задач является корректное отображение таблиц. Компания «Kozilla», в которой вы работаете, планирует разработать новую версию браузера «Waterrat» для работы в терминальном режиме и просит вас написать фрагмент ядра отображения веб-страниц, ответственный за формирование структуры таблиц.
Фрагмент, который вы должны написать, получает на вход информацию о количестве строк таблицы и ячейках этих строк и должен сгенерировать структуру таблицы и передать ее модулю, который занимается отображением таблицы на экране.
Таблица состоит из строк, каждая строка состоит из одной или нескольких ячеек, j-я ячейка i-й строки имеет ширину ai, j.
По заданным параметрам таблицы постройте символическое изображение ее структуры.
В первой строке вводится число n – количество строк в таблице ( 1![]() n
n![]() 100). Каждая из следующих n строк входных данных описывает одну строку таблицы.
100). Каждая из следующих n строк входных данных описывает одну строку таблицы.
Описание строки включает число mi – количество ячеек в этой строке, и mi целых чисел ai, 1, ai, 2,..., ai, mi – ширину каждой из ячеек строки ( 1![]() mi
mi![]() 10, 1
10, 1![]() ai, j
ai, j![]() 20).
20).
Выведите символическое изображение структуры таблицы.
Изображение i-й строки таблицы должно начинаться горизонтальной линией, составленной из символов «+» (плюс) и «-» (минус). Затем должна следовать строка, содержащая пробелы и символы «|» (вертикальная черта). Первым символом строки должна быть вертикальная черта, затем ai, 1 пробелов, затем вертикальная черта, затем ai, 2 пробелов, и так далее, всего mi блоков пробелов. После последнего блока должна следовать вертикальная черта.
После последней строки таблицы также должна следовать горизонтальная линия.
В изображении горизонтальной линии используйте символ «+», если сверху или снизу от этой позиции находится вертикальная черта, и «-» в противном случае. Горизонтальная черта должна иметь минимальную возможную длину, чтобы над каждым символом вертикальной черты следующей строки и под каждым символом вертикальной черты предыдущей строки были символы «+».
4 3 3 5 1 1 2 1 2 2 5 1
+---+-----+-+ | | | | +--++-----+-+ | | +--+ | | +--+--+-+ | | | +-----+-+
Ребята во дворе решили поиграть в прятки. Чтобы выбрать ведущего, который будет искать, они решили воспользоваться считалкой. Считалка состоит из k слов и используется следующим образом.
Все n ребят становятся в круг, и один из них, начиная с себя, по очереди указывает на ребят в порядке, в котором они стоят по кругу, называя слова считалки. Тот, на кого указывает считающий, называя последнее слово считалки, выбывает из круга. После этого считалка повторяется сначала, а счет начинается со следующего за выбывшим. Так продолжается до тех пор, пока в круге не останется один человек. Он то и будет ведущим.
Но на этот раз ребята так увлеклись идеей предстоящей игры, что забывали выходить из круга после того, как считающий указывал на них, называя последнее слово считалки. В результате считающий снова указывал на них при следующих повторениях считалки.
Ребята заметили это только тогда, когда после очередного повторения считалки считающий снова указал на последнем слове на участника, который уже должен был покинуть круг. Теперь их заинтересовал вопрос – а на скольких ребят в этот момент считающий все еще не указал, что они должны покинуть круг.
Помогите им ответить на этот вопрос.
Вводятся два целых числа – n и k ( 1![]() n
n![]() 1000, 1
1000, 1![]() k
k![]() 109).
109).
Выведите одно число – количество ребят, на которых ведущий еще не указал, что они должны покинуть круг, когда ведущий повторно укажет на кого-либо на последнем слове считалки.
6 14
3
6 13
0
Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.
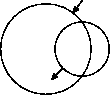
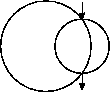
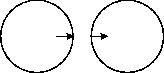
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.
Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.
Будем считать, что в городе введена прямоугольная декартова система координат.
Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.
Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.
Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.
Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.
0 0 5 4 0 3 3.0 4.0 1.878679656440357 -2.121320343559643
8.4875540166
0 0 5 4 0 3 4.0 3.0 4.0 -3.0
6.4350110879
0 0 4 10 0 4 4.0 0.0 6.0 0.0
-1
Неудовлетворенный стандартным календарем своей операционной системы, Витя решил написать программу, которая будет выводить красиво отформатированный календарь. Он разработал формальные требования к календарю, но понял, что сам не способен написать соответствующую программу. Помогите ему.
Календарь состоит из блоков, каждый из которых соответствует одному месяцу. Блоки расположены в виде таблицы из k столбцов и 12/k строк (k выбирается делителем числа 12). Месяцы выводятся в следующем порядке: первая строка содержит блоки, соответствующие месяцам с первого по k-ый, следующая – с (k + 1)-го по 2k-ый, и т. д.
Ширина всех блоков в столбце должна быть одинакова, высота всех блоков равна семи (числу дней в неделе). Между блоками различных строк таблицы выводится пустая строка, в каждой строке между соседними блоками из разных столбцов выводится три пробела.
Блок, соответствующий месяцу, устроен следующим образом. Каждой (в том числе неполной) неделе данного месяца в блоке соответствует столбец, имеющий ширину, равную двум. Между двумя соседними столбцами в каждой строке выводится один пробел. Если несколько блоков располагаются в одном столбце календаря, то для выравнивания ширины в те блоки, которые содержат меньше недель, в конец добавляется необходимое число пустых столбцов-недель. При этом разные столбцы календаря могут иметь разную ширину.
Все числа месяца заносятся в блок, соответствующий этому месяцу. Число заносится строку блока, соответствующую дню недели, на который приходится число в этом месяце. Число заносится в столбец блока, соответствующий неделе, к которой относится данное число. Однозначные числа дополняются слева одним пробелом. Таким образом, числа в столбце оказываются выравнены по правому краю.
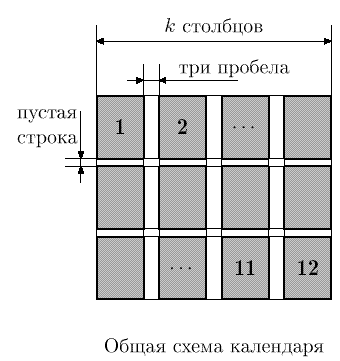 | 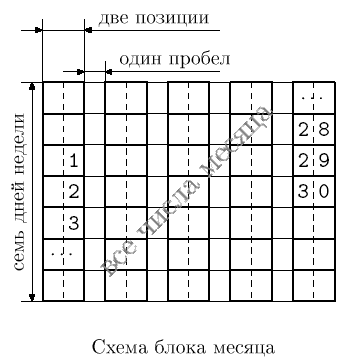 | |
| Общая схема календаря | Схема блока месяца |
На вход прораммы поступает описание года, календарь для которого следует вывести. Оно содержит три числа: d – день недели, на который приходится первое января ( 1![]() d
d![]() 7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).
7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).
Напомним, что високосный год отличается от обычного тем, что в високосном году февраль содержит 29 дней.
Выведите календарь, отформатированный в соответствии с условием задачи. Проверяющая программа в этой задаче игнорирует пробелы в конце строк. В остальном календарь должен быть отформатирован в точности так, как описано в условии.
4 1 4
5 12 19 26 2 9 16 23 1 8 15 22 29 5 12 19 26
6 13 20 27 3 10 17 24 2 9 16 23 30 6 13 20 27
7 14 21 28 4 11 18 25 3 10 17 24 31 7 14 21 28
1 8 15 22 29 5 12 19 26 4 11 18 25 1 8 15 22 29
2 9 16 23 30 6 13 20 27 5 12 19 26 2 9 16 23 30
3 10 17 24 31 7 14 21 28 6 13 20 27 3 10 17 24
4 11 18 25 1 8 15 22 29 7 14 21 28 4 11 18 25
3 10 17 24 31 7 14 21 28 5 12 19 26 2 9 16 23 30
4 11 18 25 1 8 15 22 29 6 13 20 27 3 10 17 24 31
5 12 19 26 2 9 16 23 30 7 14 21 28 4 11 18 25
6 13 20 27 3 10 17 24 1 8 15 22 29 5 12 19 26
7 14 21 28 4 11 18 25 2 9 16 23 30 6 13 20 27
1 8 15 22 29 5 12 19 26 3 10 17 24 31 7 14 21 28
2 9 16 23 30 6 13 20 27 4 11 18 25 1 8 15 22 29
6 13 20 27 4 11 18 25 1 8 15 22 29 6 13 20 27
7 14 21 28 5 12 19 26 2 9 16 23 30 7 14 21 28
1 8 15 22 29 6 13 20 27 3 10 17 24 1 8 15 22 29
2 9 16 23 30 7 14 21 28 4 11 18 25 2 9 16 23 30
3 10 17 24 1 8 15 22 29 5 12 19 26 3 10 17 24 31
4 11 18 25 2 9 16 23 30 6 13 20 27 4 11 18 25
5 12 19 26 3 10 17 24 31 7 14 21 28 5 12 19 26