#421

Изображение таблицы

Темы: [Задачи на моделирование] [Строки]

Источники: [ Командные олимпиады, ВКОШП, 2005, Задача I ]

Задана таблица в виде количества строк. Для каждой строки задано количество ячеек в ней и ширина каждой из ячеек. Необходимо нарисовать таблицу псевдографикой (знаками -, +, |).

Максимальное время работы на одном тесте: 2 секунды

При разработке программ для просмотра веб-страниц одной из наиболее сложных задач является корректное отображение таблиц. Компания «Kozilla», в которой вы работаете, планирует разработать новую версию браузера «Waterrat» для работы в терминальном режиме и просит вас написать фрагмент ядра отображения веб-страниц, ответственный за формирование структуры таблиц.

Фрагмент, который вы должны написать, получает на вход информацию о количестве строк таблицы и ячейках этих строк и должен сгенерировать структуру таблицы и передать ее модулю, который занимается отображением таблицы на экране.

Таблица состоит из строк, каждая строка состоит из одной или нескольких ячеек, j-я ячейка i-й строки имеет ширину a_{i, j}.

По заданным параметрам таблицы постройте символическое изображение ее структуры.

Входные данные

В первой строке вводится число n – количество строк в таблице ( 1 $le$ n $le$ 100). Каждая из следующих n строк входных данных описывает одну строку таблицы.

Описание строки включает число m_i – количество ячеек в этой строке, и m_i целых чисел a_{i, 1}, a_{i, 2},..., a_{i, m_i} – ширину каждой из ячеек строки ( 1 $le$ m_i $le$ 10, 1 $le$ a_{i, j} $le$ 20).

Выходные данные

Выведите символическое изображение структуры таблицы.

Изображение i-й строки таблицы должно начинаться горизонтальной линией, составленной из символов «+» (плюс) и «-» (минус). Затем должна следовать строка, содержащая пробелы и символы «|» (вертикальная черта). Первым символом строки должна быть вертикальная черта, затем a_{i, 1} пробелов, затем вертикальная черта, затем a_{i, 2} пробелов, и так далее, всего m_i блоков пробелов. После последнего блока должна следовать вертикальная черта.

После последней строки таблицы также должна следовать горизонтальная линия.

В изображении горизонтальной линии используйте символ «+», если сверху или снизу от этой позиции находится вертикальная черта, и «-» в противном случае. Горизонтальная черта должна иметь минимальную возможную длину, чтобы над каждым символом вертикальной черты следующей строки и под каждым символом вертикальной черты предыдущей строки были символы «+».

Примеры

Входные данные

Выходные данные

+---+-----+-+
|   |     | |
+--++-----+-+
|  |
+--+
|  |
+--+--+-+
|     | |
+-----+-+

#422

Неправильная считалка

Темы: [НОД и алгоритм Евклида]

Источники: [ Командные олимпиады, ВКОШП, 2005, Задача J ]

N человек стоит в круге. Длина считалки K - слов. Игроки не выходят, если считалка закончилась на них. Требуется определить на скольких людях считалка не кончалась, когда она впервые закончится второй раз на каком-либо человеке.

Ребята во дворе решили поиграть в прятки. Чтобы выбрать ведущего, который будет искать, они решили воспользоваться считалкой. Считалка состоит из k слов и используется следующим образом.

Все n ребят становятся в круг, и один из них, начиная с себя, по очереди указывает на ребят в порядке, в котором они стоят по кругу, называя слова считалки. Тот, на кого указывает считающий, называя последнее слово считалки, выбывает из круга. После этого считалка повторяется сначала, а счет начинается со следующего за выбывшим. Так продолжается до тех пор, пока в круге не останется один человек. Он то и будет ведущим.

Но на этот раз ребята так увлеклись идеей предстоящей игры, что забывали выходить из круга после того, как считающий указывал на них, называя последнее слово считалки. В результате считающий снова указывал на них при следующих повторениях считалки.

Ребята заметили это только тогда, когда после очередного повторения считалки считающий снова указал на последнем слове на участника, который уже должен был покинуть круг. Теперь их заинтересовал вопрос – а на скольких ребят в этот момент считающий все еще не указал, что они должны покинуть круг.

Помогите им ответить на этот вопрос.

Входные данные

Вводятся два целых числа – n и k ( 1 $le$ n $le$ 1000, 1 $le$ k $le$ 10⁹).

Выходные данные

Выведите одно число – количество ребят, на которых ведущий еще не указал, что они должны покинуть круг, когда ведущий повторно укажет на кого-либо на последнем слове считалки.

Примеры

Входные данные

6 14

Выходные данные

Входные данные

6 13

Выходные данные

#423

В школу на велосипеде

Темы: [Алгоритм Дейкстры] [Элементарная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2004, Задача A ]

Даны две пересекающихся окружности. Необходимо найти кратчайший путь от точки до точки по окружностям.

Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.

В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.

Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.

Входные данные

Будем считать, что в городе введена прямоугольная декартова система координат.

Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.

Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10^-8). Точки могут лежать как на одной дорожке, так и на разных.

Выходные данные

Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10^-4.

Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.

Примеры

Входные данные

0 0 5
4 0 3
3.0 4.0
1.878679656440357 -2.121320343559643

Выходные данные

8.4875540166

Входные данные

Выходные данные

6.4350110879

Входные данные

Выходные данные

-1

#424

Календарь

Темы: [Дата и время] [Строки]

Источники: [ Командные олимпиады, ВКОШП, 2004, Задача B ]

По известному первому дню года, високосности года, количеству столбцов в календаре необходимо напечатать календарь.

Неудовлетворенный стандартным календарем своей операционной системы, Витя решил написать программу, которая будет выводить красиво отформатированный календарь. Он разработал формальные требования к календарю, но понял, что сам не способен написать соответствующую программу. Помогите ему.

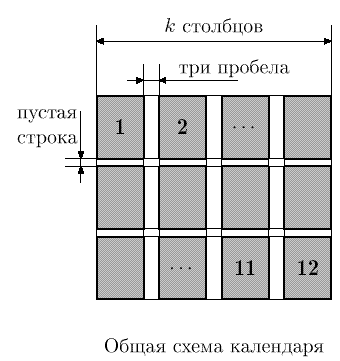
Календарь состоит из блоков, каждый из которых соответствует одному месяцу. Блоки расположены в виде таблицы из k столбцов и 12/k строк (k выбирается делителем числа 12). Месяцы выводятся в следующем порядке: первая строка содержит блоки, соответствующие месяцам с первого по k-ый, следующая – с (k + 1)-го по 2k-ый, и т. д.

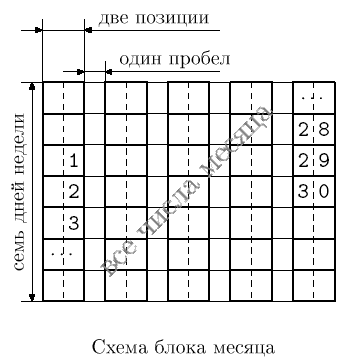
Ширина всех блоков в столбце должна быть одинакова, высота всех блоков равна семи (числу дней в неделе). Между блоками различных строк таблицы выводится пустая строка, в каждой строке между соседними блоками из разных столбцов выводится три пробела.

Блок, соответствующий месяцу, устроен следующим образом. Каждой (в том числе неполной) неделе данного месяца в блоке соответствует столбец, имеющий ширину, равную двум. Между двумя соседними столбцами в каждой строке выводится один пробел. Если несколько блоков располагаются в одном столбце календаря, то для выравнивания ширины в те блоки, которые содержат меньше недель, в конец добавляется необходимое число пустых столбцов-недель. При этом разные столбцы календаря могут иметь разную ширину.

Все числа месяца заносятся в блок, соответствующий этому месяцу. Число заносится строку блока, соответствующую дню недели, на который приходится число в этом месяце. Число заносится в столбец блока, соответствующий неделе, к которой относится данное число. Однозначные числа дополняются слева одним пробелом. Таким образом, числа в столбце оказываются выравнены по правому краю.



Общая схема календаря		Схема блока месяца

Входные данные

На вход прораммы поступает описание года, календарь для которого следует вывести. Оно содержит три числа: d – день недели, на который приходится первое января ( 1 $le$ d $le$ 7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).

Напомним, что високосный год отличается от обычного тем, что в високосном году февраль содержит 29 дней.

Выходные данные

Выведите календарь, отформатированный в соответствии с условием задачи. Проверяющая программа в этой задаче игнорирует пробелы в конце строк. В остальном календарь должен быть отформатирован в точности так, как описано в условии.

Примеры

Входные данные

4 1 4

Выходные данные

    5 12 19 26          2  9 16 23    1  8 15 22 29       5 12 19 26   
    6 13 20 27          3 10 17 24    2  9 16 23 30       6 13 20 27   
    7 14 21 28          4 11 18 25    3 10 17 24 31       7 14 21 28   
 1  8 15 22 29          5 12 19 26    4 11 18 25       1  8 15 22 29   
 2  9 16 23 30          6 13 20 27    5 12 19 26       2  9 16 23 30   
 3 10 17 24 31          7 14 21 28    6 13 20 27       3 10 17 24      
 4 11 18 25          1  8 15 22 29    7 14 21 28       4 11 18 25      
                                                                       
    3 10 17 24 31       7 14 21 28       5 12 19 26       2  9 16 23 30
    4 11 18 25       1  8 15 22 29       6 13 20 27       3 10 17 24 31
    5 12 19 26       2  9 16 23 30       7 14 21 28       4 11 18 25   
    6 13 20 27       3 10 17 24       1  8 15 22 29       5 12 19 26   
    7 14 21 28       4 11 18 25       2  9 16 23 30       6 13 20 27   
 1  8 15 22 29       5 12 19 26       3 10 17 24 31       7 14 21 28   
 2  9 16 23 30       6 13 20 27       4 11 18 25       1  8 15 22 29   
                                                                       
    6 13 20 27          4 11 18 25    1  8 15 22 29       6 13 20 27   
    7 14 21 28          5 12 19 26    2  9 16 23 30       7 14 21 28   
 1  8 15 22 29          6 13 20 27    3 10 17 24       1  8 15 22 29   
 2  9 16 23 30          7 14 21 28    4 11 18 25       2  9 16 23 30   
 3 10 17 24          1  8 15 22 29    5 12 19 26       3 10 17 24 31   
 4 11 18 25          2  9 16 23 30    6 13 20 27       4 11 18 25      
 5 12 19 26          3 10 17 24 31    7 14 21 28       5 12 19 26

#425

Военный поход

Темы: [Алгоритм Дейкстры]

Источники: [ Командные олимпиады, ВКОШП, 2004, Задача C ]

В неориентированном графе, где для ребра указана его стоимость, мы владеем некоторым набором ребер. Необходимо купить все дороги по маршруту и продать часть своих дорог.

В одном феодальном государстве средневековой Европы было n городов и m дорог, каждая из которых соединяла некоторые два города. Каждая дорога принадлежала правителю одного из городов (не обязательно одного из тех, которые она соединяла). Однажды правитель города S решил объявить войну правителю города T. Перед ним сразу же встала нелегкая задача: как довести армию до города T.

Правитель каждого города требует плату за проход войск через его город. Кроме того, правитель города S может перемещать войска только по дорогам, которые принадлежат ему. При этом он может купить любую дорогу у ее владельца за определенную плату (даже если владелец – правитель города T). К сожалению, все деньги из казны города S были потрачены на предыдущий неудачный военный поход, поэтому сначала правителю придется продать некоторые свои дороги (разумеется, после этого он не сможет провести по ним войска).

Помогите правителю выяснить, какие дороги следует продать, а какие купить, чтобы довести войска от города S до города T и оплатить проход через все промежуточные города. Все операции продажи и покупки дорог надо осуществить до начала похода, пока правители других городов не догадались о воинственных намерениях правителя города S.

Входные данные

В первой строке вводятся целые числа n и m – количество городов и дорог соответственно ( 2 $le$ n $le$ 2 000, 1 $le$ m $le$ 50 000). Города нумеруются от 1 до n, города S и T имеют номера 1 и n соответственно.

Следующие n строк содержат под одному целому числу r_i – плату за проезд через город i ( 0 $le$ r_i $le$ 10 000, r₁ = r_n = 0).

Далее идут m строк, задающих описания дорог. Дорога описывается четырьмя целыми числами: a_i, b_i, p_i и c_i. Здесь a_i и b_i – номера городов, которые соединяет дорога, p_i – номер города, правителю которого она принадлежит, c_i – ее стоимость ( a_i $ne$ b_i, 1 $le$ c_i $le$ 10 000). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более, чем одной дорогой.

Выходные данные

В первой строке выведите список дорог, которые нужно продать в следующем формате: сначала число дорог, а затем их номера. Дороги нумеруются с единицы в том порядке, в котором они заданы во входных данных. Во второй строке выведите список дорог, которые нужно купить, в том же формате. В третьей строке выведите маршрут похода – номера городов в порядке следования войска. Если решений несколько, выведите любое.

Если решения нет, выведите число -1.

Примеры

Входные данные

Выходные данные

2 1 2
1 3
1 3