Из правил проведения студенческого командного чемпионата мира по программированию ACM:

Когда команда считает, что она решила задачу, она может послать свое решение на проверку. Решение проверяется на наборе секретных тестов. Если хотя бы один из тестов не проходит, команде сообщается причина (неверный ответ, превышение предела времени и т.д.). Такое решение считается неверным и на результат команды никак не влияет.

Если же решение проходит все тесты, то данная задача считается решенной, и команде начисляется некоторое количество штрафного времени. Штрафное время — это время в минутах от начала тура до момента посылки правильного решения этой задачи на проверку плюс по 20 штрафных минут за каждую неверную попытку по этой задаче (до тех пор, пока решение не прошло все тесты, никакого штрафного времени за задачу не начисляется).

Команды ранжируются по числу решенных задач, а при одинаковом их числе — по штрафному времени (чем штрафное время меньше, тем лучше).

Задача:

Жюри точно уверено, что команда «Super solvers», известная своей непобедимостью, все равно за тур успеет решить все задачи, и, скорее всего, каждую из задач — с первой же попытки (то есть штрафное время за каждую задачу будет равно времени от начала тура до момента ее посылки на проверку). Конечно, жюри может попытаться усложнить задачи, однако оно не хочет этого делать, так как опасается, что в этом случае из остальных команд вообще никто ничего не решит.

Сама команда тоже прекрасно понимает, что ей по силам решить все задачи, поэтому ей все равно, в каком порядке решать задачи — и команда решила, что будет решать задачи по порядку, начиная с первой.

Среди членов жюри есть тренер этой команды. Он прознал про тактику, которой решила придерживаться команда, а также может примерно оценить время, которое потребуется команде для решения каждой задачи. Жюри прекрасно понимает, что уже никак не может повлиять на число решенных командой задач, но зато, учитывая тактику команды, жюри может влиять на штрафное время, которое получит команда, располагая задачи в разном порядке. В самом деле, если на тур предлагается две задачи, и на решение одной из них команда тратит 10 минут, а на решение второй — 20, то штрафное время команды, если задачи расположить именно в таком порядке, будет равно 40 минутам (первую задачу команда сдает на 10-й минуте тура, вторую — на 30, 10+30=40). Если же задачи расположить в обратном порядке, то штрафное время будет равно 50 (сначала команда потратит 20 минут, потом еще 10, то есть пошлет задачи на 20-й и 30-й минутах, и штрафное время будет равно 20+30=50).

Жюри хочет, чтобы штрафное время команды «Super solvers» было как можно больше (быть может, это даст хоть какой-то шанс другим командам). Помогите членам жюри расположить задачи в таком порядке.

«Что наша жизнь? Игра!»

Вася в казино играет в интересную игру.

Сначала он платит вступительный взнос за игру и в обмен на деньги получает право играть. Более того, за уплаченные деньги он сразу получает X очков.

На автомате, в который он играет, есть три кнопки. Когда он нажимает первую, к его очкам добавляется A очков. Когда нажимает вторую — добавляется B. Когда нажимает третью — добавляется C очков.

Ему разрешается сначала несколько раз (или ни разу) нажать третью кнопку, и затем несколько раз (или ни разу) — первую. Нажимать вторую кнопку Васе запрещено.

Если после этого он набрал ровно Y очков, то Вася считается выигравшим, и ему выплачивается премия. Если же Y очков набрать не удается, Вася считается проигравшим, и ничего не получает.

Если Вася выиграл, то считается, что он разгадал одну из волшебных последовательностей нажатий, которые приводят к выигрышу. Он имеет право и дальше играть в эту игру, и искать другие такие последовательности, которые X очков превращают в Y, но ему категорически запрещено использовать одну и ту же выигрышную последовательность более одного раза.

Напишите программу, которая посчитает, сколько различных выигрышных последовательностей существует, то есть сколько раз Вася может выиграть в эту замечательную игру.

Задачи противовоздушной обороны: ...борьба с десантом на всем маршруте пролета,

уничтожение вертолетов огневой поддержки, действующих из засады»

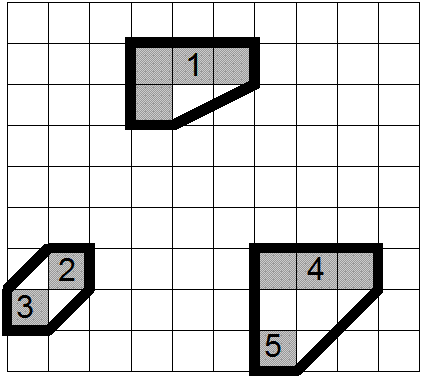Радиолокационная станция (РЛС) состоит из нескольких передатчиков (не более 5). К сожалению, их нельзя ставить рядом — они друг для друга создают помехи. Каждый передатчик состоит из квадратных модулей, которые располагаются вплотную друг к другу.

Вам дана карта района, в котором расположена РЛС. Вся карта для удобства разбита на квадраты, и для каждого квадрата известно, располагается в нем какой-то из модулей одного из передатчиков РЛС или нет.

Требуется оградить забором (или несколькими заборами) минимально возможной суммарной длины все передатчики РЛС. Забор — это произвольная ломаная (ее элементы не обязаны идти по сторонам клеток). Одним забором могут быть огорожены сразу несколько передатчиков.