Страница: << 1 2 3 4 5 >> Отображать по:
#855
Сортировка вагонов
  
Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

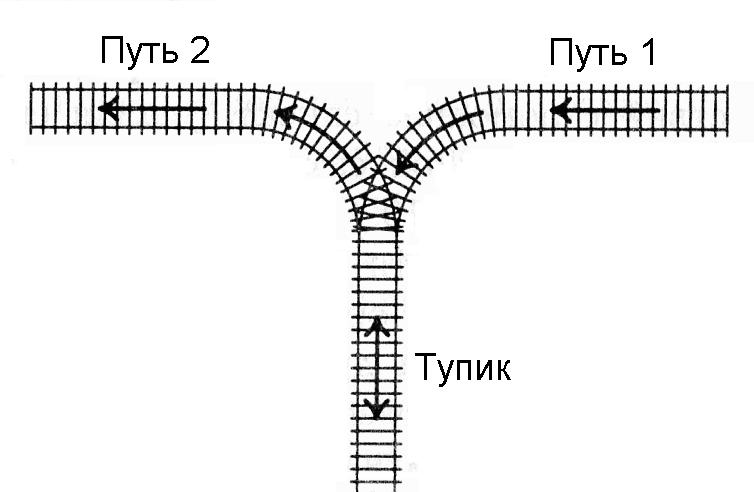
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

  • если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
  • если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0
#1132
Шахматы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
На доске стоят слоны и ладьи. Необходимо подсчитать, сколько клеток не бьет ни одна из фигур.

На шахматной доске стоит несколько офицеров и ладей. Требуется посчитать количество свободных клеток, которые не находятся под боем ни одной из фигур.

Замечание для тех, кто не умеет играть в шахматы:

Шахматная доска имеет размеры 8*8. Ладья бьет все клетки горизонтали и вертикали, проходящих через клетку, где она стоит, до первой встретившейся фигуры. Офицер бьет все клетки обеих диагоналей, проходящих через клетку, где он стоит, до первой встретившейся фигуры.

Входные данные

В первых восьми строках входного файла описывается шахматная доска. Первые восемь символов каждой из этих строк описывают состояние соответствующей горизонтали: символ B (заглавная латинская буква) означает, что в клетке стоит офицер, символ R — ладья, символ * — что клетка пуста. После описания горизонтали в строке могут идти пробелы, однако длина каждой строки не превышает 250 символов. После описания доски в файле могут быть пустые строки.

Выходные данные

В выходной файл выведите количество пустых клеток, которые не бьются ни одной из фигур.

Примеры
Входные данные
********
********
*R******
********
********
********
********
********
Выходные данные
49
Входные данные
********
********
******B*
********
********
********
********
********
Выходные данные
54
#1193
Оцените пассажиропоток
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Маршрут автобуса проходит через N остановок (включая конечные). Отдел по исследованию пассажиропотоков записал данные о том, сколько человек выходило и сколько садилось в автобус на каждой остановке. Напишите программу, которая по этим данным определит, какое максимальное количество человек одновременно в этот рейс ехало в автобусе.

Входные данные

Во входном файле записано сначала число N (2≤N≤100) – количество остановок на маршруте. Далее задается количество человек, севших в автобус на конечной. Далее идет (N-2) пары чисел, задающих для промежуточных остановок количество вышедших и количество вошедших пассажиров. Наконец, идет число, задающее количество вышедших из автобуса на конечной остановке.

Количество вошедших пассажиров на каждой остановке не превышало 100. Данные корректны, в частности, суммарное количество вошедших в автобус на всех остановках пассажиров всегда равно суммарному количеству вышедших.

Выходные данные

В выходной файл выведите одно целое число — максимальное количество человек, которые в какой-то момент одновременно ехали в автобусе.

Комментарии к примерам тестов

1. На конечной в автобус село 10 человек. Далее 3 вышло и 1 зашел. В автобусе стало 8 человек. На следующей остановке вышло 5 и зашло 10. Стало 13 человек. На последней промежуточной остановке никто не вышел, а зашло 2 человека. На конечной вышло 15 человек. Итого максимальное количество – 15.

2. На конечной село 10 человек, которые на следующей остановке вышли. После этого на следующей остановке никто не сел и никто не вышел. Дальше опять село 10 человек, которые доехали до конечной.

3. С конечной автобус отправился без пассажиров. Дальше в него село 9 человек. На следующей остановке 3 вышли и зашли 4. В автобусе стало 10 человек. На следующей остановке 2 вышли и никто не зашел. 8 человек доехало до конечной. Максимальное количество пассажиров составляло 10

4. На начальной и на промежуточной остановку в автобус село по 100 человек. Вышло из автобуса 200 человек.

Примеры
Входные данные
5
10
3 1
5 10
0 2
15
Выходные данные
15
Входные данные
5
10
10 0
0 0
0 10
10
Выходные данные
10
Входные данные
5
0 
0 9
3 4
2 0
8
Выходные данные
10
Входные данные
3
100
0 100
200
Выходные данные
200
#1241
Черно-белые палиндромы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Дана полоса клетчатой бумаги длиной N клеток и шириной 1 клетка, в которой некоторые клетки покрашены в черный цвет, а остальные — в белый. Такая полоса называется палиндромом, если последовательность черных и белых клеток при просмотре этой полосы слева направо оказывается такой же, как при просмотре справа налево.

Вам дана полоса длины N. Требуется разрезать ее на полоски, являющиеся палиндромами, так, чтобы количество получившихся полосок было строго меньше величины (2/5)N + 3.

Входные данные

Первая строка входного файла содержит число N — длину исходной полосы (N — натуральное число, не превышающее 100000). Далее идет N чисел, описывающих раскраску полосы: 0 означает черную клетку, а 1 — белую.

Выходные данные

В выходной файл выведите в возрастающем порядке номера клеток исходной полосы, после которых нужно сделать разрезы.

Примеры

Входные данные

Выходные данные

Пояснение

6

0 1 0 1 1 0

3 5

Из исходной полосы мы получим 3 полосы-палиндрома, сделав разрезы после 3-й клетки (то есть между 3-й и 4-й) и после 5-й (то есть между 5-й и 6-й)

6

0 1 1 0 0 0

1 3

Данную полосу можно разрезать на 2 полосы-палиндрома, однако по условию не требуется искать решение с минимальным числом получившихся полосок — достаточно, чтобы число полосок удовлетворяло указанному в условии ограничению.

5

0 0 0 0 0


Исходная строка уже является палиндромом, поэтому можно ничего не разрезать
#1242
Луч света в темном царстве
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Темное царство представляет собой лабиринт NxM, некоторые клетки которого окружены зеркальными стенами, а остальные — пустые. Весь лабиринт также окружен зеркальной стеной. В одной из пустых клеток лабиринта поставили светофор, который испускает лучи в 4 направлениях: под 45 градусов относительно стен лабиринта. Требуется изобразить траекторию этих лучей.

Когда луч приходит в угол, через который проходят зеркальные стены, дальше он идет так, как показано на рисунках (серым цветом показаны клетки, которые окружены зеркальными стенами). Аналогичным образом луч ведет себя, когда приходит на границу лабиринта.


Входные данные

В первой строке входного файла записаны два натуральных числа N и M — число строк и столбцов в лабиринте (каждое из чисел не меньше 1 и не больше 100). В следующих N строках записано ровно по M символов в каждой — карта лабиринта. Символ * (звездочка) обозначает клетку, окруженную зеркальными стенками, . (точка) — пустую клетку, символ X (заглавная латинская буква X) — клетку, в которой расположен светофор (такая клетка ровно одна).

Выходные данные

В выходной файл выведите N строк по M символов в каждой — изображение лабиринта с траекториями лучей. Здесь, как и раньше, * (звездочка) должна обозначать клетки, окруженные зеркальными стенами, . (точка) — пустые клетки, через которые лучи света не проходят, / (слеш) — клетки, через которые луч света проходит из левого нижнего угла в правый верхний (или обратно — из правого верхнего в левый нижний), \ (обратный слеш) — клетки, через которые луч проходит из левого верхнего угла в правый нижний (или обратно), а символ X (заглавная латинская буква X) — клетки, через которые лучи проходят по обеим диагоналям.

Примеры
Входные данные
3 5
X....
.....
.....
Выходные данные
XXXXX
XXXXX
XXXXX
Входные данные
3 3
...
..X
...
Выходные данные
/X\
X.X
\X/
Страница: << 1 2 3 4 5 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест