Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#428
Фермерские будни
  
Источники: [ Командные олимпиады, ВКОШП, 2004, Задача F ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На плоскости заданы 4 многоугольника со сторонами, параллельными осям координат. Необходимо разбить плоскость вертикальной или горизонтальной прямой так, чтобы в каждой части оказалось по 2 прямоугольника.

Год назад Флатландию потряс серьезный экономический кризис, после которого, с целью снижения издержек, фермер Джон и фермер Билл решили объединить свои фермы. За год совместной продуктивной работы на объединенной территории было построено четыре сарая.

Однако последствия кризиса в последнее время ощущаются все меньше, да и совместное ведение хозяйства – дело непростое. Поэтому фермеры решили снова разделить свои фермы.

Для раздела ферм решено было построить забор. Разумеется, прежде чем приступить к строительству, фермеры взяли карту совместного хозяйства и стали обсуждать возможное положение забора. Забор должен представлять собой прямую линию. Поскольку по закону границы участков должны быть направлены либо с севера на юг, либо с запада на восток, забор на карте должен представлять собой прямую, параллельную краю карты – вертикальную либо горизонтальную.

Единственная проблема – четыре построенных за год совместной работы сарая. Разумеется, каждому фермеру в результате раздела должно достаться по два сарая. Поэтому после постройки забора два сарая должны оказаться с одной стороны от него, а два других – с другой.

Помогите фермерам найти такое положение для забора. Забор может проходить непосредственно вдоль стены сарая.

Входные данные

На вход программы поступают четыре четверки целых чисел. Каждая четверка описывает один сарай. Первые два числа в описании сарая – это координаты на карте его левого нижнего угла, следующие два числа – координаты правого верхнего угла.

Система координат размещена таким образом, что ось OX направлена слева направо, а ось OY – снизу вверх. Оси координат параллельны краям карты. Стороны сараев также параллельны краям карты. Сараи не имеют общих точек. Каждый сарай имеет ненулевую площадь. Все координаты неотрицательны и не превышают 109.

Выходные данные

Если построить забор, удовлетворяющий всем условиям, невозможно, выведите   слово «Impossible».

В противном случае в первой строке выведите слово «Vertical», если забор следует построить параллельно вертикальному краю карты, или слово «Horizontal», если забор следует построить параллельно горизонтальному краю карты.

В следующей строке выведите координату x всех точек забора, если он должен быть вертикальным, либо координату y всех точек забора, если он должен быть горизонтальным. Выведенная координата должна быть целым числом (несложно показать, что если забор можно построить, то его можно построить так, чтобы искомая координата была целой).

Приведенные ниже рисунки соответствуют примерам входных данных.

 

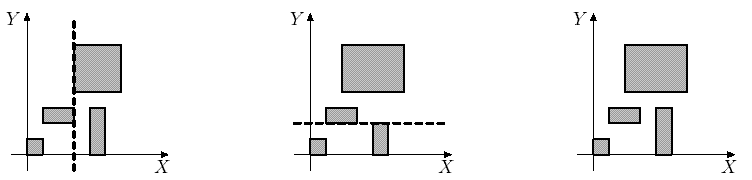
includegraphics{pics/farm.1}
Примеры
Входные данные
0 0 1 1
1 2 3 3
4 0 5 3
3 4 6 7
Выходные данные
Vertical
3
Входные данные
0 0 1 1
1 2 3 3
4 0 5 2
2 4 6 7
Выходные данные
Horizontal
2
Входные данные
0 0 1 1
1 2 3 3
4 0 5 3
2 4 6 7
Выходные данные
Impossible
#431
Восстановление программы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Задана последовательность команд "поворот налево" и "поворот направо". Требуется каждой команде сопоставить число шагов, чтобы путь не пересекал и не касался самого себя.

Выполняя очередное задание Министерства образования и сельского хозяйства, программисты Флатландского государственного университета информационных технологий, удобрений и ядохимикатов создали специального робота по прокладке оросительных каналов.

Программа для робота представляет собой последовательность команд. Команды робота приведены в следующей таблице:

 

Команда

Обозначение

Действия робота

Перемещение

(X)

Переместиться вперед на X километров, прокладывая за собой оросительный канал
Поворот налево L Повернуть налево на 90o
Поворот направо

R

Повернуть направо на 90o

Любая программа начинается и заканчивается командами перемещения и не содержит двух команд перемещения или двух команд поворота подряд.

Исходно робот размещается в некоторой точке поля, на котором требуется создать оросительную систему. После запуска робот последовательно выполняет команды своей программы. Программа считается корректной, если полученный в результате ее выполнения канал не имеет самопересечений или самокасаний.

Программисты университета написали программу и собрались отправить ее по электронной почте в министерство. Однако, в результате поражения сети университета вирусом программа оказалась испорчена. А именно, из нее исчезли все команды перемещения. Теперь программистам требуется восстановить программу. Поскольку времени очень мало, решено было оставить сохранившиеся команды поворота, вставив между ними команды перемещения так, чтобы получившаяся программа была корректной.

Входные данные

Входные данные содержат команды поворота исходной программы в том порядке, в котором они в ней следовали. Каждая команда представляет собой символ «L» либо «R», команды друг от друга не отделяются. Количество команд не превышает 30 000.

Выходные данные

Выведите  любую корректную программу, последовательность команд поворота в которой совпадает с последовательностью, заданной во входных данных. Параметр X каждой команды перемещения должен быть положительным целым числом и не должен превышать 109. Все команды выведите в одной строке и друг от друга не отделяйте.

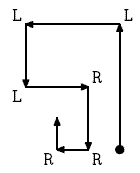
includegraphics{pics/program.1}
Примеры
Входные данные
LLLRRR
Выходные данные
(4)L(3)L(1)L(2)R(2)R(1)R(1)
#503
Календарь
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Календарь на июнь 2007 года, висящий у меня на стене, выглядит следующим образом:
Пн Вт Ср Чт Пт Сб Вс
                    1   2   3
4   5   6   7   8   9  10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
В этом календаре числа располагаются в 5 строк. Вам требуется написать программу, которая определит, сколько строк чисел будет в подобном календаре на любой заданный месяц.

Входные данные

Вводятся два числа \(D\) и \(F\).
\(D\) – количество дней в месяце, натуральное число от 28 до 31.
\(F\) – номер дня недели, на который приходится первое число данного месяца (1 – понедельник, 2 – вторник, … , 7 – воскресенье).

Выходные данные

Выведите количество строк чисел в календаре на указанный месяц.

Примеры
Входные данные
30 5
Выходные данные
5
#504
И снова лифт
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В торговом центре этажи нумеруются так: …, –3, –2, –1, 1, 2, 3, … (нулевого этажа нет!). Вася спустился на лифте с этажа с номером \(A\) на \(B\) этажей, а затем поднялся на лифте на \(C\) этажей. Требуется определить, на каком этаже он оказался.

Входные данные

Вводятся три числа \(A\), \(B\) и \(C\).
\(А\) – целое число от –100 до 100, не равное нулю.
\(B\) и \(С\) – натуральные числа, не превосходящие 100.

Выходные данные

Выведите одно число – номер этажа, на котором окажется Вася.

Примеры
Входные данные
5 1 1
Выходные данные
5
Входные данные
-5 1 1
Выходные данные
-5
#520
Упаковка
  
Источники: [ Командные олимпиады, ВКОШП, 2003, Задача E ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Даны размеры контейнера (в трех измерениях) и двух коробок. Необходимо определить, помещаются ли коробки в контейнер, если верх обязательно должен совпадать и боковые грани должны быть параллельны граням контейнера.

В одну транспортную компанию поступил заказ на перевозку двух ящиков из одного города в другой. Для перевозки ящики решено было упаковать в специальный контейнер.

Ящики и контейнер имеют вид прямоугольных параллелепипедов. Длина, ширина и высота первого ящика – \(l_1\), \(w_1\) и \(h_1\), соответствующие размеры второго ящика – \(l_2\), \(w_2\) и \(h_2\). Контейнер имеет длину, ширину и высоту \(l_c\), \(w_c\) и \(h_c\).

Поскольку ящики содержат хрупкое оборудование, после упаковки в контейнер каждый из них должен остаться в строго вертикальном положении. Таким образом, ящики можно разместить рядом или один на другом. Для надежного закрепления в контейнере стороны ящиков должны быть параллельны его сторонам. Иначе говоря, если исходно ящики были расположены так, что все их стороны параллельны соответствующим сторонам контейнера, то каждый из них разрешается перемещать и поворачивать относительно вертикальной оси на угол, кратный 90 градусам.

Разумеется, после упаковки оба ящика должны полностью находиться внутри контейнера и не должны пересекаться.

Выясните, можно ли поместить ящики в контейнер с соблюдением указанных условий.

Входные данные

Первая строка входных данных содержит \(l_1\), \(w_1\) и \(h_1\), вторая – \(l_2\), \(w_2\) и \(h_2\), третья – \(l_c\), \(w_c\) и \(h_c\). Все размеры – целые положительные числа, не превышающие 1000. Числа в строках разделены пробелами.

Выходные данные

Выведите YES, если ящики можно упаковать в контейнер, и NO в противном случае.

Пояснения к примерам

В первых двух примерах ящики можно разместить рядом, при этом во втором один из них следует повернуть на 90 градусов. В третьем примере ящики можно разместить один на другом. В четвертом примере первый ящик слишком высокий и не влезает в контейнер. В пятом примере ящики нельзя разместить ни рядом, ни один на другом.

Примеры
Входные данные
2 2 3
3 3 3
3 5 3
Выходные данные
YES
Входные данные
2 3 3
3 2 3
4 4 4
Выходные данные
YES
Входные данные
4 1 2
3 3 2
4 3 4
Выходные данные
YES
Входные данные
1 1 4
1 1 3
10 10 3
Выходные данные
NO
Входные данные
3 2 2
3 1 2
5 2 3
Выходные данные
NO
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест