Сегодня Игорь получил долгожданное разрешение на проведение эксперимента по изучению протекания химических реакций в магнитном поле. При этом используются две установки – генератор магнитного поля и манипулятор, соединяющий реагенты.

Эксперимент разбит на некоторое количество этапов, при этом некоторые из них могут быть выполнены только после завершения определенного набора других этапов. Правда известно, что хотя бы один способ проведения эксперимента существует. На каждом этапе Игорь должен управлять ровно одной из двух установок – либо генератором, либо манипулятором.

Игорь очень дорожит своим временем, и поэтому он хочет провести эксперимент, совершив наименьшее количество перемещений между пультами управления установками. Помогите ему узнать, в каком порядке следует выполнять этапы, чтобы этого добиться.

Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.

Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.

Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.

Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.

Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:

 

1. если вершина красная, то ее родитель – черный;
2. количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.

Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.

 

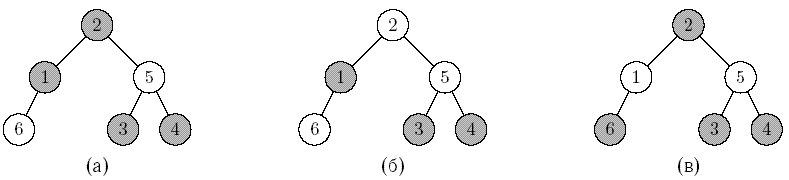Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.

Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.

Сверхсекретный завод, расположенный высоко в горах, занимается изготовлением новейших систем контроля торсионных полей – нанокристаллов. Нанокристалл состоит из нескольких атомов, некоторые из которых попарно связаны сверхпрочными торсионными связями.

Нанокристалл стабилен, если между любыми двумя его атомами можно построить соединяющую их цепочку связей, возможно с использованием других атомов. Например, нанокристалл из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.

Для любой пары атомов стабильного нанокристалла определена их взаимная удаленность – минимальная длина цепочки из связей, которая их соединяет. Например, рассмотрим описанный выше нанокристалл . Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).

Важнейшей характерикой стабильного нанокристалла является его емкость. Емкость нанокристалла равна сумме взаимных удаленностей всех пар его атомов. Например, емкость нанокристалла  равна 8.

Недавно на завод поступил заказ – разработать стабильный нанокристалл заданной емкости c. При этом как число атомов в нанокристалле, так и число связей может быть произвольным. Помогите ученым разработать такой кристалл!

Недавно Билл устроился на работу полицейским. Теперь ему предстоит каждый вечер обходить свой участок, который представляет собой прямоугольник, состоящий из N×M кварталов. Каждый квартал имеет вид квадрата размером 100×100 метров, кварталы отделены друг от друга прямыми улицами.

Таким образом, через участок Билла проходит \(N\) + 1 улица, идущая с запада на восток и \(M\) + 1 улица, идущая с севера на юг. Перекрестки разбивают улицы на (\(N\) + 1)\(M\) + (\(M\) + 1)\(N\) отрезков, каждый из которых имеет длину 100 метров.

Совершая обход, Билл выходит из полицейского управления, расположенного около юго-западного угла его участка, обходит свой участок и возвращается в управление. Во время обхода Билл должен пройти по каждому отрезку улицы на территории своего участка как минимум один раз. Известно, что во время обхода Билл проходит отрезок длиной 100 метров за одну минуту. Выясните, какое минимальное число минут потребуется Биллу, чтобы совершить обход.

Каждый раз, когда в мире происходит значимое событие, наша реальность разветвляется на несколько — в зависимости от исхода этого события. После этого существует уже не только наша основная реальность, но и ответвившиеся от неё в моменты появления разных исходов.

Однажды один архимаг решил сделать мир лучше. Такая грандиозная задача не под силу одному архимагу, поэтому он решил найти самого себя ещё в K реальностях и выполнить эту задачу вместе. Проведённое теоретическое исследование показало, что, кроме реальности, в которой находится именно он, существует ещё N - 1 реальностей. Для удобства они были занумерованы числами от 1 до N, при этом его собственная реальность имеет номер 1, а посетить ему необходимо реальности с номерами 2, 3, ..., K + 1.

Как уже говорилось, каждая реальность когда-то ответвилась от некоторой другой, за исключением одной Начальной реальности, которая существовала всегда (её номер может оказаться каким угодно; считается, что она появилась в момент времени 0). Исследование показало, что реальность с номером i ответвилась от реальности с номером P_i в момент времени T_i. Из каждой реальности с номером i архимаг может переместиться

• в любую ответвившуюся от неё, то есть в любую j, такую что P_j = i;
• в P_i, если i — не Начальная реальность.

Другими словами, возможны лишь переходы вида i <-> P_i. На каждый такой переход в любую сторону архимаг затрачивает T_i - T_Pi > 0 условных единиц энергии.

Требуется найти минимальное количество энергии, которое потребуется архимагу, чтобы, начав в реальности с номером 1, посетить все реальности с номерами от 2 до K + 1 (в любом порядке) и затем вновь вернуться в 1. Любую реальность при этом разрешается посещать сколько угодно раз.