На соревнованиях по прыжкам на лыжах с трамплина техника прыжка оценивается пятью судьями. Каждый судья ставит оценку от \(1\) до \(20\), после чего одна наименьшая и одна наибольшая оценки отбрасываются. Вам нужно написать программу, которая будет демонстрировать результаты прыжка для телетрансляции.
Она должна выводить пять оценок, которые поставили судьи, не меняя их порядка, а затем их сумму, и при этом брать в скобки те оценки, которые не учитываются при расчете суммы
На вход подается \(5\) натуральных чисел от \(1\) до \(20\), разделенных пробелом.
Выведите те же числа в том же порядке, взяв в скобки минимальное (а если их несколько – самое левое из них) и максимальное (а если их несколько – самое правое из них) число, а также сумму всех чисел, не взятых в скобки. Все числа (включая сумму) должны быть напечатаны в одной строке и разделены одним пробелом (внутри скобок пробелов быть не должно). Перед суммой должен стоять знак равенства, отделенный слева и справа одним пробелом. Порядок оценок должен быть такой же, как и во входных данных.
1 2 3 4 5
(1) 2 3 4 (5) = 9
10 11 10 11 10
(10) 11 10 (11) 10 = 31
Магическим квадратом называют таблицу, в которой записаны числа \(1, 2, 3, …\) по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной \((3\times 3, 5\times 5, …)\).
Поставим число \(1\) в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа \(2, 3, 4, …\). Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов \(3\times 3\) и \(5\times 5\) показаны на рисунках.
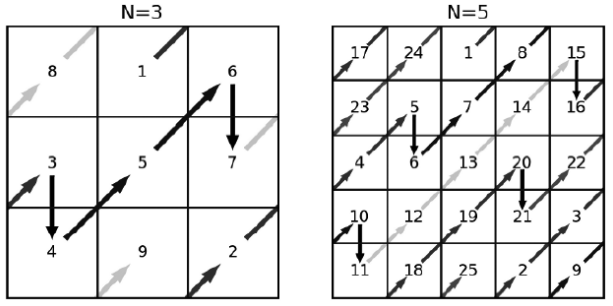
На вход подается одно натуральное нечетное число \(N\), не превосходящее \(30\) – размер квадрата.
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
3
8 1 6 3 5 7 4 9 2
5
17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9
Дано N золотых слитков. Требуется распилить не более одного из них на две части (не обязательно равные, но с целой массой), после чего разделить слитки на две кучи равной массы.
В первой строке вводится одно натуральное число N, не превосходящее 100.
Во второй строке через пробел вводятся N натуральных чисел, не превосходящих 100 - массы имеющихся слитков.
Выведите массы слитков, которые вошли в первую кучку (включая массу части распиленного слитка).
Если решений несколько, выведите любое из них.
Если решений нет, выведите фразу NO SOLUTION (заглавными буквами).
Выводить массы можно в произвольном порядке, но масса части распиленного слитка (если таковой имеется) должна быть последней.
3 5 5 5
NO SOLUTION
4 1 2 3 8
1 2 3 1
4 1 2 3 8
1 2 3 1
Васе подарили два ежедневника на i-й год. Один он использовал в i-м году и теперь интересуется, когда наступит следующий год с точно таким же календарем, чтобы он мог воспользоваться вторым ежедневником.
Вводится одно натуральное число i, не превышающее 2011.
Выведите одно число - номер года, когда можно будет использовать второй ежедневник.
2011
2022
1
7
Сколько всего натуральных чисел состоят из не менее чем a цифр и не более, чем b цифр?
Вводятся два произвольных натуральных числа a и b через пробел. Каждое не превышает 10000.
Выведите одно число: количество чисел, обладающих указанным свойством.
1 2
99
1 1
9