--->
3 задач
<---
Страница:
1
Отображать по:
#235
Темы:
[Целые числа]
[Условный оператор (if)]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Решите в целых числах уравнение:
\(\sqrt{ax+b} = c\),
a, b, c – данные целые числа: найдите все решения или сообщите, что решений в целых числах нет.
Входные данные
Вводятся три числа a, b и c, разделенные пробелами.
Выходные данные
Программа должна вывести все решения уравнения в порядке возрастания, либо NO SOLUTION (заглавными буквами), если решений нет. Если решений бесконечно много, вывести MANY SOLUTIONS.
Примеры
Входные данные
1 0 0
Выходные данные
0
Входные данные
1 2 -3
Выходные данные
NO SOLUTION
#236
Темы:
[Целые числа]
[Условный оператор (if)]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Натуральные числа записаны в (бесконечную) таблицу, как показано на рисунке.
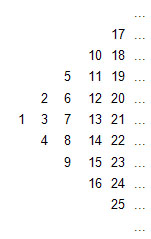
Требуется по заданному числу вывести всех его соседей (числа, записанные в клетках сверху, справа, слева и снизу, если таковые имеются)
Входные данные
Вводится одно натуральное число, не превосходящее \(10^9\).
Выходные данные
Программа должна вывести все числа, записанные в соседних клетках с данным, в порядке возрастания. Числа должны разделяться пробелом.
Примеры
Входные данные
1
Выходные данные
3
Входные данные
7
Выходные данные
3 6 8 13
#2766
Темы:
[Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Два автомобиля движутся по кольцевой дороге длины \(L\) в противоположных направлениях. Они начинают движение из одной точки и едут с постоянными скоростями \(v_1\) и \(v_2\) соответственно. Требуется определить, на каком расстоянии друг от друга они окажутся в момент времени \(T\).
Входные данные
На вход подаются \(4\) натуральных числа \(L\), \(v_1\), \(v_2\), \(T\), разделенных пробелом. Все числа не превосходят \(100\).
Выходные данные
Выведите расстояние между автомобилями в момент времени \(T\) – длину кратчайшей из двух дуг дороги между автомобилями.
Примеры
Входные данные
10 1 2 1
Выходные данные
3
Входные данные
10 2 3 2
Выходные данные
0
Страница:
1
Отображать по:
Выбрано
:
|