Страница: 1 2 >> Отображать по:
#235
Уравнение
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Решите в целых числах уравнение:

 \(\sqrt{ax+b} = c\),

a, b, c – данные целые числа: найдите все решения или сообщите, что решений в целых числах нет.

Входные данные

Вводятся три числа a, b и c, разделенные пробелами.

Выходные данные

Программа должна вывести все решения уравнения в порядке возрастания, либо NO SOLUTION (заглавными буквами), если решений нет. Если решений бесконечно много, вывести MANY SOLUTIONS. 

Примеры
Входные данные
1 0 0
Выходные данные
0
Входные данные
1 2 -3
Выходные данные
NO SOLUTION
#236
Бесконечная таблица
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Натуральные числа записаны в (бесконечную) таблицу, как показано на рисунке.

1

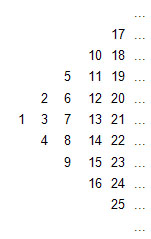
Требуется по заданному числу вывести всех его соседей (числа, записанные в клетках сверху, справа, слева и снизу, если таковые имеются)

Входные данные

Вводится одно натуральное число, не превосходящее \(10^9\).

Выходные данные

Программа должна вывести все числа, записанные в соседних клетках с данным, в порядке возрастания. Числа должны разделяться пробелом.

Примеры
Входные данные
1
Выходные данные
3
Входные данные
7
Выходные данные
3 6 8 13
#502
Ресторан
  
Темы: [Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В одном курином ресторане можно купить
1 ножку + 1 крыло,
1 ножку + 1 бедро,
1 бедро,
2 крыла,
или 3 крыла.
Требуется определить, можно ли купить ровно \(k\) крыльев, \(n\) ножек и \(b\) бедер.

Входные данные

Вводятся три числа \(k\), \(n\), \(b\). Все числа целые неотрицательные, не превосходящие 100.

Выходные данные

Выведите слово YES, если купить указанный набор можно, NO – если нельзя (заглавными латинскими буквами).

Примеры
Входные данные
0 6 0
Выходные данные
NO
Входные данные
2 3 1
Выходные данные
YES
#534
Ваня наблюдает за лягушкой
  
Темы: [Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Ваня наблюдает за лягушкой. Изначально она сидит в точке 0 числовой прямой. Каждую секунду она прыгает на 1 вправо, пока не достигнет точки K. Затем она начинает каждую секунду прыгать на 1 влево, пока не вернется в точку 0, затем – опять вправо и т. д. Требуется определить, где окажется лягушка через T секунд.

Входные данные

Вводятся два числа \(K\) и \(T\), разделенные пробелом. Оба числа натуральные и не превосходят 1 000 000 000.

Выходные данные

Вывести одно число – координату лягушки в момент времени \(T\).

Примеры
Входные данные
10 6
Выходные данные
6
#1233
Двоякие числа
  
Темы: [Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Натуральное число называется двояким, если в его десятичной записи встречается не более двух различных цифр. Например, числа 3, 23, 33, 100, 12121 — двоякие, а числа 123 и 9980 — нет.

Для заданного натурального числа N требуется найти ближайшее к нему двоякое число (если таких чисел два — любое из них).

Входные данные

Во входном файле записано одно натуральное число N, не превосходящее 30 000.

Выходные данные

В выходной файл требуется выдать единственное число — ближайшее двоякое к числу N.

Примеры
Входные данные
123
Выходные данные
122
Входные данные
2012
Выходные данные
2020
Входные данные
11111
Выходные данные
11111
Страница: 1 2 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест