#532

Коля решает уравнение

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача H ]

Помогите Коле решить уравнение Уравнение. a / $x^2$ + b / x + c = 0

Входные данные

Вводятся три числа $a$, $b$, $c$, разделенные пробелами. Все числа целые и по модулю не превосходят 100.

Выходные данные

Требуется вывести все различные корни уравнения (по одному разу в любом порядке). Выведенные корни должны отличаться от точного ответа не более, чем на 0,01. Если уравнение не имеет корней, вывести No solution.

Если уравнение имеет больше 10 корней, вывести Many solutions.

Примеры

Входные данные

1 2 1

Выходные данные

-1.0000000000

#533

Витя и Денис играют в игру \"Быки и коровы\

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача I ]

Витя и Денис играли в игру «Быки и коровы». Витя загадал четырёхзначное число с неповторяющимися цифрами, а Денис пытался это число угадать. Для этого он предлагал свои четырёхзначные числа (тоже с неповторяющимися цифрами), а Витя про каждое из них сообщал, сколько в нём «быков» (т. е. цифр, которые не только присутствуют и в Витином числе, и в числе Дениса, но даже стоят на одних и тех же местах) и «коров» (цифр, которые присутствуют в обоих числах, но стоят на разных местах). У них осталась запись партии (последовательность тестовых чисел и ответов на них), но задуманное число утратилось. Восстановите задуманное число.

Входные данные

Вводится сначала число \)N$ — количество четырёхзначное чисел, названных Денисом в одной партии ($N \le 100$). Затем вводятся $N$ строк, по три числа в каждой. Первое — четырёхзначное число, названное Денисом (оно не начинается с нуля), второе — количество «быков», третье — количество «коров».

Выходные данные

Требуется вывести одно четырёхзначное число, задуманное Витей. Это число не начинается с 0.

Гарантируется, что ответ в задаче существует и является единственным.

Примеры

Входные данные

Выходные данные

#534

Ваня наблюдает за лягушкой

Темы: [Целые числа]

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача J ]

Ваня наблюдает за лягушкой. Изначально она сидит в точке 0 числовой прямой. Каждую секунду она прыгает на 1 вправо, пока не достигнет точки K. Затем она начинает каждую секунду прыгать на 1 влево, пока не вернется в точку 0, затем – опять вправо и т. д. Требуется определить, где окажется лягушка через T секунд.

Входные данные

Вводятся два числа $K$ и $T$, разделенные пробелом. Оба числа натуральные и не превосходят 1 000 000 000.

Выходные данные

Вывести одно число – координату лягушки в момент времени $T$.

Примеры

Входные данные

10 6

Выходные данные

#854

Складирование ноутбуков

Темы: [Простые задачи на перебор]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2008, Лига А, Задача A ]

На склад, который имеет форму прямоугольного параллелепипеда, привезли ноутбуки, упакованные в коробки. Каждая коробка также имеет форму прямоугольного параллелепипеда.

По правилам хранения коробки с ноутбуками должны быть размещены на складе с выполнением следующих двух условий:

Стороны коробок должны быть параллельны сторонам склада

Коробку при помещении на склад разрешается расположить где угодно (с выполнением предыдущего условия), в том числе на другой коробке, но все коробки должны быть ориентированы одинаково (т.е. нельзя одну коробку расположить «стоя», а другую – «лежа»)

Напишите программу, которая по размерам склада и размерам коробки с ноутбуком определит максимальное количество ноутбуков, которое может быть размещено на складе.

Входные данные

Вводится шесть натуральных чисел. Первые три задают длину, высоту и ширину склада. Следующие три задают соответственно длину, высоту и ширину коробки с ноутбуком. Каждое из чисел не превышает 1000.

Выходные данные

Выведите одно число — максимальное количество ноутбуков, которое может быть размещено на складе.

Примеры

Входные данные	Выходные данные
100 200 300 1 2 3	1000000
100 200 300 3 2 1	1000000
100 100 1 2 2 2	0
7 7 7 3 3 3	8

#855

Сортировка вагонов

Темы: [Стек] [Задачи на моделирование]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2008, Лига А, Задача B ]

Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

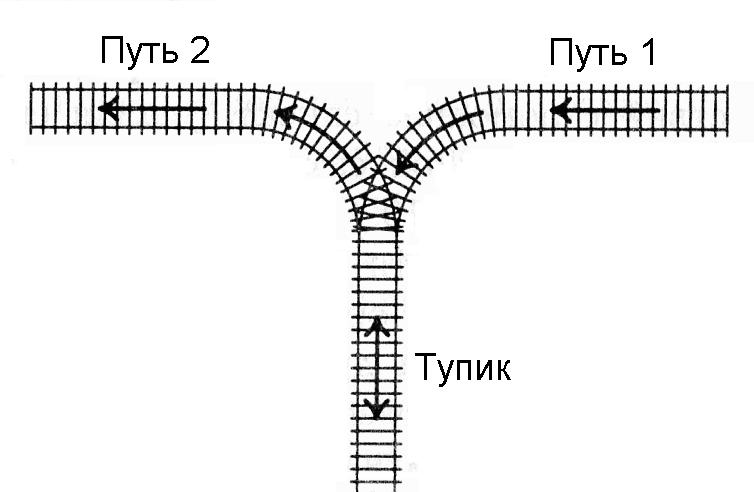
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0