Родители подарили мальчику Пете очень много одинаковых кубиков. Наиболее интересным сооружением из кубиков Петя счел двусторонние лесенки.
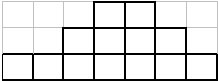
В основании (нижнем ряду) такой лесенки расположено \(N\) кубиков, а каждый следующий ряд кубиков укладывается на предыдущий так, что один кубик укладывается ровно на один нижестоящий кубик, а по крайней мере на самый правый и самый левый кубики предыдущего ряда новые кубики не кладутся (чтобы получилась ступенька).
Петя поручил старшему брату подсчитать, сколько можно построить различных лесенок, состоящих из ровно \(K\) рядов кубиков, в основании которых лежит ровно \(N\) кубиков. При этом, если одну лесенку можно получить из другой путем зеркального отображения, то они все равно считаются различными.
Вводятся два числа \(N\) и \(K\) (\(1 \le N \le 100\), \(1 \le K \le 100\)).
Выведите одно число – количество различных лесенок. Гарантируется, что правильный ответ не будет превышать \(10^{18}\).
10 4
84
Петя каждый день ездит на работу на метро по одному и тому же маршруту с двумя пересадками. Он уже давно запомнил, сколько времени занимает проезд на нужном ему отрезке пути по каждой из трех линий. Также он выучил расписание поездов на всех трех линиях, по которым он ездит. Помогите Пете найти такое время входа в метро, чтобы поездка на работу занимала как можно меньше времени.
В первой строке вводятся времена поездки по первой, второй и третьей линии (до пересадки) в минутах. Все времена – натуральные числа и не превышают 1140 минут. Считается, что пересадка не занимает времени.
Во второй строке вводятся количество поездов на первой линии, на второй линии и на третьей линии – натуральные числа, не превосходящие 100.
В третьей строке вводятся времена отправления поездов первой линии со станции, на которой садится Петя (по два числа на каждый поезд – часы и минуты).
В четвертой строке в том же формате вводятся времена отправления поездов второй линии со станции, на которую Петя делает первую пересадку.
В пятой строке – аналогичное расписание поездов третьей линии со станции, на которую Петя делает вторую пересадку.
Находиться в метро с часу ночи до 6 часов утра запрещается (в 6 часов утра на поезд садиться можно). Расписание движения поездов таково, что Петя может добраться до работы, не выходя из метро.
Выведите время (часы и минуты), в которое Петя может войти в метро, чтобы добраться до работы за наименьшее время. Если решений несколько, выведите любое из них.
10 20 30 2 2 2 10 0 12 0 11 0 15 0 12 0 19 0
10 0
В парикмахерской работают три мастера. Каждый тратит на одного клиента ровно полчаса, а затем сразу переходит к следующему, если в очереди кто-то есть, либо ожидает, когда придет следующий клиент.
Даны времена прихода клиентов в парикмахерскую (в том порядке, в котором они приходили). Требуется для каждого клиента указать время, когда он выйдет из парикмахерской.
В первой строке вводится натуральное число N, не превышающее 100 – количество клиентов.
Гарантируется, что всех клиентов успеют обслужить до полуночи.
Требуется вывести N пар чисел: времена выхода из парикмахерской 1-го, 2-го, …, N-го клиента (часы и минуты).
3 10 0 10 1 10 2
10 30 10 31 10 32
Пароль называется криптостойким, если он включает в себя и строчные латинские буквы, и заглавные латинские буквы, и цифры, при этом его длина должна быть не менее 8 символов.
Требуется по данному паролю определить, является ли он криптостойким.
Вводится одна строка, состоящая только из латинских букв и цифр. Количество символов в строке не превышает 100.
Выведите слово YES, если указанный пароль является криптостойким, и NO – в противном случае (заглавными латинскими буквами).
1
NO
q
NO
В одном курином ресторане можно купить
1 ножку + 1 крыло,
1 ножку + 1 бедро,
1 бедро,
2 крыла,
или 3 крыла.
Требуется определить, можно ли купить ровно \(k\) крыльев, \(n\) ножек и \(b\) бедер.
Вводятся три числа \(k\), \(n\), \(b\). Все числа целые неотрицательные, не превосходящие 100.
Выведите слово YES, если купить указанный набор можно, NO – если нельзя (заглавными латинскими буквами).
0 6 0
NO
2 3 1
YES