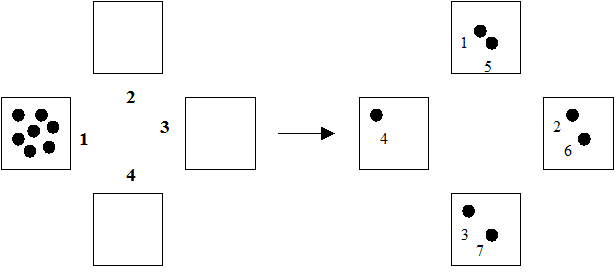
Для игры в калах используют несколько коробочек, расставленных по кругу, в которых лежат шарики. Ход осуществляется следующим образом. Берутся все шарики из одной коробочки, и начинают раскладываться по одному в коробочки подряд начиная со следующей по часовой стрелке. Если шариков больше, чем коробочек, то процесс продолжается (шарики раскладываются по второму кругу, по третьему и т.д.), пока не будут разложены все шарики. В коробочку, из которой взяли шарики, их тоже кладут. Пример одного хода приведен на рисунке. Справа шарики пронумерованы в том порядке, в котором они раскладывались по коробочкам.

Петя, тренируясь перед соревнованиями, разложил шарики по коробочкам произвольным образом, и стал делать произвольные ходы. После каждого хода он записывал номер коробочки, в которую попадал последний шарик. В некоторый момент он решил восстановить начальную конфигурацию по конечной и по тем записям, которые он делал. Напишите программу, которая поможет ему в этом.

Как известно, Россия является одним из ведущих экспортеров нефти. Разные страны мира, от достаточно больших до сравнительно маленьких, нуждаются в этой нефти как в воздухе. В ее состав в больших количествах входят ароматические углеводороды, которые обуславливают ее высокое качество. Доставка нефти в пункт назначения осуществляется с помощью нефтепровода. Считается, что количество нефти, отправленное в страну назначения, равно количеству полученной нефти. На самом деле это, конечно, не так. Как и многое другое, нефть воруют некоторые несознательные личности. Причем неофициально считается, что больше нефти воруют в нефтепроводах тех стран, куда нефти посылается больше (может быть, несознательные личности считают, что приносят, таким образом, меньше ущерба, кто знает...). Официальное руководство компании РусскаяНефть решило узнать, правдивый это слух или нет, чтобы усилить (а может просто установить) охрану на тех нефтепроводах, где больше всего воруют нефть.

Для этого им нужно отсортировать нефтепроводы по количеству нефти, которая протекает в направлении какой-то страны за сутки. У компании РусскаяНефть, как и у любой уважающей себя компании, есть несколько штатных программистов, и руководство предложило им решить эту, в сущности, нетрудную задачу. Но программистов поставило в тупик то, что данные о количестве нефти представлены в разных единицах измерения (начиная от граммов и заканчивая тоннами).

Поэтому они решили найти человека, который был бы в силах решить эту задачу за них, и обещают взять его на работу в эту перспективную и процветающую компанию. Решите задачу, и, кто знает, может, повезет именно Вам?

На некоторой железнодорожной ветке расположено N станций, которые последовательно пронумерованы числами от 1 до N. Известны расстояния между некоторыми станциями. Требуется точно вычислить длины всех перегонов между соседними станциями или указать, что это сделать невозможно (то есть приведенная информация является противоречивой или ее недостаточно).

У калькулятора есть две ячейки памяти: содержимое первой из них всегда отображается на табло, вторая является буфером. В начальный момент времени на табло калькулятора отображается целое число X, а в буфере записано число 0. У калькулятора работают только две клавиши: «+» и «=». При нажатии на «+» число, которое в данный момент отображено на табло, копируется в буфер. При нажатии на «=» число из буфера прибавляется к числу, отображенному на табло и результат отображается на табло, число в буфере при этом не меняется.

Требуется за наименьшее число нажатий клавиш на калькуляторе добиться того, чтобы на табло было отображено число Y.

Петя, изучая, как меняется курс рубля по отношению к доллару и евро, вывел закон, по которому происходят эти изменения (или думает, что вывел). По этому закону Петя рассчитал, каков будет курс рубля по отношению к доллару и евро в ближайшие N дней.

У Пети есть 100 рублей. В каждый из дней он может обменивать валюты друг на друга по текущему курсу без ограничения количества (при этом курс доллара по отношению к евро соответствует величине, которую можно получить, обменяв доллар на рубли, а потом эти рубли — на евро). Поскольку Петя будет оперировать не с наличной валютой, а со счетом в банке, то он может совершать операции обмена с любым (в том числе и нецелым) количеством единиц любой валюты.

Напишите программу, которая вычисляет, какое наибольшее количество рублей сможет получить Петя к исходу N-го дня.

Законы изменения курсов устроены так, что в течение указанного периода рублевый эквивалент той суммы, которая может оказаться у Пети, не превысит 10⁸ рублей.