Командная олимпиада, о которой идёт речь в этой задаче, проходила по тем же правилам, что и олимпиада, в которой вы сейчас участвуете. Возможно, за одним исключением: на ней было введено ограничение на суммарное число посылок от одной команды, которые можно было потратить как на одну задачу, так и распределить их по всем задачам некоторым образом.
Как и сегодня, за час до окончания олимпиады таблица результатов была «заморожена». Каково же было удивление участников, когда при подведении итогов выяснилось, что в окончательной таблице все команды расположились строго в обратном порядке (по отношению к порядку, зафиксированному «заморозкой»). Так как в окончательной таблице результатов посылки участников не отражены, вам предлагается определить, могло ли такое быть в принципе, или это результат технического сбоя системы.
Первая строка содержит три натуральных числа: N — количество команд, K — количество задач, L — лимит на суммарное число посылок по задачам (N ≤ 1000, K ≤ 12, K ≤ L ≤ 200).
Далее следуют N строк, описывающих саму таблицу на момент заморозки. i-я строка содержит название команды (строка из латинских символов и цифр длины не более 50) и K элементов, показывающих успех команды по каждой из задач. j-й элемент таблицы имеет вид * Wrong(Time), где:
* — знак ‘ + ’ или ‘ - ’, показывающий, решила ли команда задачу;
Wrong — количество неуспешных посылок по данной задаче;
Time — минута, на которой команда сдала задачу (0 ≤ Time ≤ 239); если данная задача ещё не была решена, Time = 0.
Команды упорядочены от первого места на момент заморозки к последнему. Напоминаем, что команды сортируются по числу решённых задач, а при равном количестве — по увеличению штрафного времени, которое складывается из времени сдачи задачи и общего количества неудачных попыток по решённым задачам, умноженного на 20. Продолжительность олимпиады — 5 часов.
Гарантируется, что ни одна команда не превысила лимит на число посылок и что никакие две команды не имеют одинаковый с точки зрения сортировки результат.
Если порядок команд теоретически мог измениться за последний час соревнований на обратный, то сначала выведите строку «Possible», а затем подробную таблицу окончательных результатов в формате, аналогичном таблице из входного файла (см. пример). Если соревнование так закончиться не могло, то выведите единственную строку «Impossible».
3 3 10
winner +2(235) +3(170) -2(0)
middle -2(0) +1(30) -0(0)
looser -1(0) +5(30) -0(0)
Possible
looser +1(240) +5(30) +0(240)
middle +5(241) +1(30) +0(240)
winner +2(235) +3(170) +2(240)
2 2 20
winner +10(1) +0(10)
looser -0(0) +1(1)
Impossible
Спортивный программист для достижения вершин своего мастерства должен быть натренирован в совершенно разных аспектах, в том числе и физически. Кто-то для этого садится на велосипед, кто-то ныряет в бассейн, а молодой программист Влад бегает по стадиону. Но из-за неаккуратного обращения с личными вещами его секундомер может измерять время только в минутах, без указания секунд и тем более их долей.
Чтобы следить за прогрессом своего ученика, тренеру Влада приходится довольствоваться показаниями этого прибора. Каждый раз, когда Влад пробегает мимо тренера, сделав очередной круг по стадиону, тот записывает в блокнот показания секундомера в минутах. Фактически показания секундомера соответствуют целому числу минут, прошедших к определенному моменту времени. Причём, если секундомер показывает, например, 1, то это может обозначать и время ровно 2 минуты, так как 1.(9) = 2.
На контрольной тренировке Влад бегал с постоянной скоростью, однако по записям тренера не так легко сказать, с какой именно. Кроме того, секундомер был, возможно, запущен до того как Влад начал бегать. Напишите программу, которая поможет тренеру определить за какое минимальное, а также максимальное возможное время Влад мог пробегать каждый круг.
В первой строке входного файла находится единственное натуральное число N — количество записей в блокноте тренера (2 ≤ N ≤ 105). В следующей строке находятся сами эти записи — разделённые пробелами целые числа a1, a2, ..., aN (0 ≤ a1 ≤ a2 ≤ ... ≤ aN ≤ 106). Здесь a1 соответствует времени, когда Влад пробежал мимо тренера в первый раз.
Выведите два неотрицательных вещественных числа, разделённых пробелом, — минимальное и максимальное возможное количество минут, за которое спортсмен пробегал один круг. Ваш ответ должен отличаться от правильного менее чем на 10 - 3.
Если ответа не существует, то есть Влад не мог бежать с постоянной скоростью так, чтобы записи тренера получились именно такими, в единственной строке выведите «No solution».
5
2 3 5 6 8
1.33333 1.66667
5
1 6 9 14 17
4 4
3
1 5 6
No solution
5
1 1 2 3 3
0.5 0.75
Во втором тесте время 4 соответствует показаниям секундомера 1.(9), 6.0, 9.(9), 14.0, 17.(9).
В четвёртом примере минимальное время соответствует показаниям секундомера 1.5, 1.(9), 2.5, 3.0, 3.5, а максимальное — показаниям 1.0, 1.75, 2.5, 3.25, 3.(9).
Как вы помните, Джонни работает в министерстве финансов одной небольшой страны. На этот раз он решил очень тщательно распланировать бюджет. Для этого ему первым делом необходимо выяснить, сколько же будет выходных дней в каждом интересующем его году (без учёта праздников, которые и в этой стране то и дело переносят).
Так как Джонни смотрит в будущее, то его интересуют лишь года, которые ещё не наступили. Но он верит в успехи биоинформатики, касающиеся увеличения продолжительности жизни, и хочет рассчитать всё заранее, поэтому его интересуют и очень отдалённые даты. При этом он предположил, что достаточно рассчитать лишь некоторые из интересующих его годов, чтобы получить общую картину.
В первой строке входного файла содержится целое число Q — количество лет, которые интересуют Джонни (1 ≤ Q ≤ 1 000 000). Далее в Q строках содержатся номера годов Yi, по одному на строке (2013 ≤ Yi ≤ 109).
Для каждого года в отдельной строке выведите количество выходных дней в соответствующем году.
1
2013
104
Напомним, что в неделе семь дней, выходными считаются суббота и воскресенье. Сегодня четырнадцатое октября две тысячи двенадцатого года, воскресенье. В невисокосных годах 365 дней, в високосных — 366. Год называется високосным, если он делится на 400, или если он делится на 4, но не делится на 100.
Максим и Лёша поехали на сборы в Петрозаводск. После тура они решили не ходить на дорешивание, а поиграть в шахматы. Игра проходит на бесконечной доске, и в какой-то момент у Максима осталось только две ладьи и король, а у Алексея — один король. А на бесконечной доске в такой ситуации победить затруднительно. Тогда Максим заменил своего короля на припасённую ещё одну ладью и ситуация изменилась.
Помогите Максиму поставить мат тремя ладьями на бесконечной доске.
Это интерактивная задача. При запуске решения на стандартный поток ввода поступают 8 чисел — координаты короля и трёх ладей на поле. Координаты не превосходят по модулю 100. Гарантируется, что в начальный момент никакие две фигуры не стоят на одной клетке, и король не находится под боем ни одной из ладей. Первый ход делает Максим.
На каждый ход Максима вводится ответный ход Алексея — перемещение короля dx, dy относительно текущей позиции (0 ≤ |dx|, |dy| ≤ 1). В случае, если |dx| = |dy| = 0, программа должна немедленно завершиться (это означает, что был поставлен мат, пат или сделан некорректный ход).
Для каждого хода выводите на стандартный поток вывода три числа — номер ладьи (1, 2 или 3) и перемещение ладьи lx, ly (|lx| + |ly| > 0;|lx|·|ly| = 0). Ход должен быть корректным, т. е. ладья не может пойти в занятую клетку, перепрыгнуть через другую фигуру. Перемещение ладьи не должно быть больше, чем на 1 000 клеток.
2 0 1 2 0 4 4 1
1 0
-1 -1
0 0
1 0 -1
2 3 0
3 -2 0
Вывод должен завершаться переводом строки и сбросом буфера потока вывода. Для этого используйте flush(output) на языке Паскаль или Delphi, fflush(stdout) или cout.flush() в С/C++, sys.stdout.flush() на языке Python, System.out.flush() на языке Java.
Программа не должна делать более 40 ходов. Если после хода программы мат не поставлен, а король сделать ход не может, то считается, что тест не пройден.
Ладья может ходить на произвольное количество клеток по горизонтали или по вертикали. Король же может ходить в любую соседнюю клетку, которая не находится под боем ладьи, в том числе, он может «съесть» ладью, если клетка, в которой ладья стоит, не находится под боем другой ладьи. Обратите внимание, что в случае, если король съест ладью, то выигрыш станет невозможным, и тест не будет пройден.
Мат — ситуация в шахматах, когда король находится под ударом ладьи, а игрок не может сделать ни одного хода, чтобы его избежать. Пат — ситуация в шахматах, когда король не находится под ударом ладьи, но при этом игрок не может сделать ни одного хода.
Обратите внимание, что тестирующая система сообщает подробный протокол взаимодействия вашей программы и программы жюри. Гарантируется, что существует программа, которая на всех тестах жюри умеет ставить мат.
Пример ответа тестирующей системы для примера из условия.
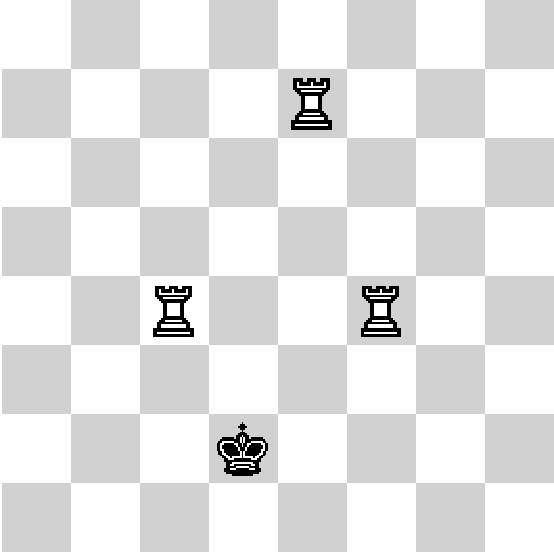
Starting position: king on (2 0), rooks on (1 2) (0 4) (4 1)
Turn 1
Max moves 1st rook to (1 1)... OK.
Alex moved king to (3 0)
King on (3 0), rooks on (1 1) (0 4) (4 1)
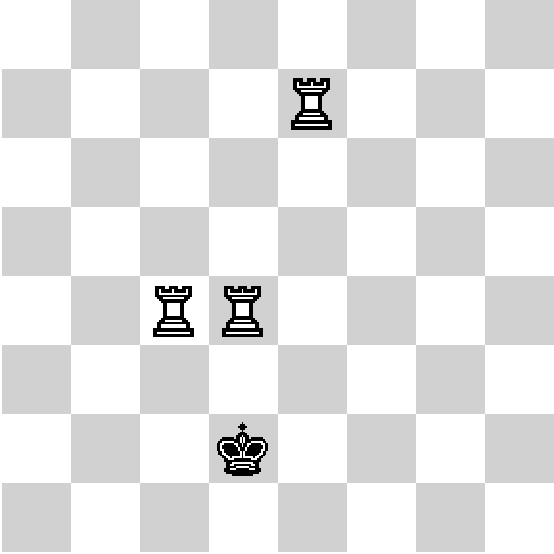
Turn 2
Max moves 2nd rook to (3 4)... OK.
Alex moved king to (2 0)
King on (2 0), rooks on (1 1) (3 4) (4 1)
Turn 3
Max moves 3rd rook to (2 1)... OK.
It's nowhere for king to go :-(
Game over! Checkmate - Max wins!
Положение фигур по ходу игры.
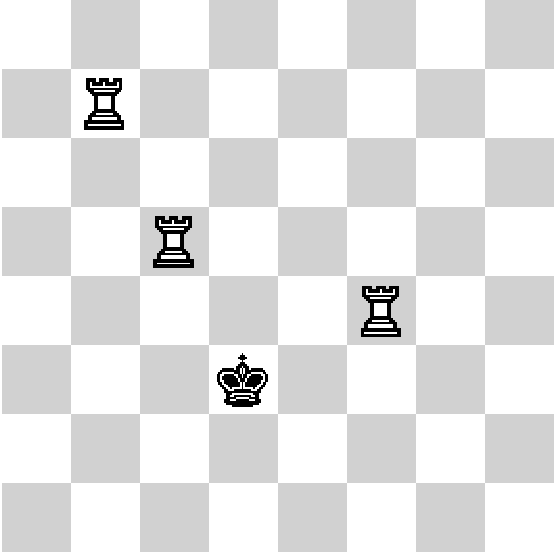
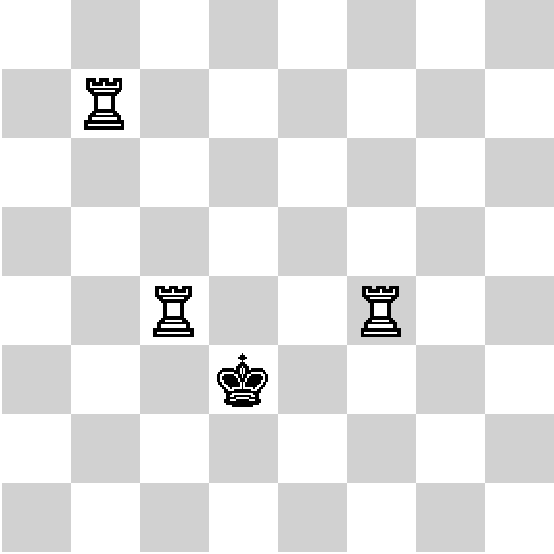
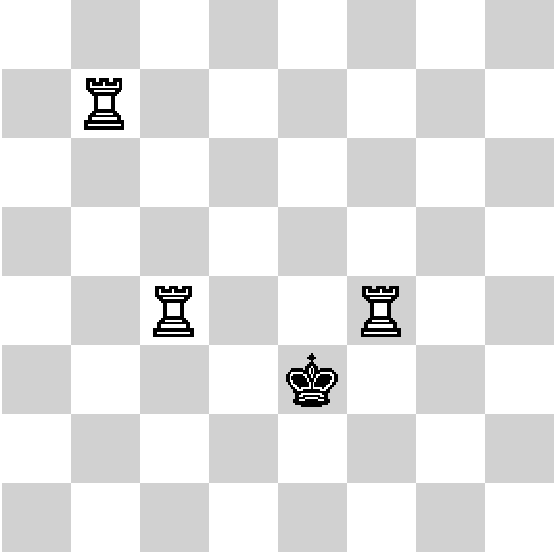
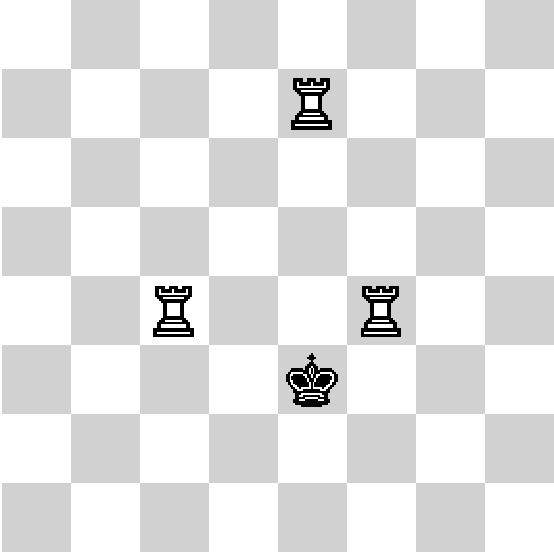
Вася играет в очень интересную игру «Jumper». На специальной дорожке в ряд расположено несколько батутов. Батуты бывают двух типов: те, которые рассчитаны на прыжки в высоту, и те, которые рассчитаны на прыжки в длину. Игрок прыгает по батутам слева направо. При этом, первый свой прыжок он обязан сделать на любом батуте, который рассчитан на прыжок в длину (чтобы хорошенько разогнаться), после этого подпрыгнуть на батуте, который предназначен для прыжков в высоту (теперь он с разгона сможет подпрыгнуть очень высоко!). Игра ограничена по времени, поэтому игрок прыгает только на два батута.
Ваша задача состоит в том, чтобы определить, сколько существует различных способов сыграть в игру. Два способа считаются различными, если они различаются хотя бы одним батутом (для прыжков в длину или для прыжков в высоту).
В единственной строке входных данных содержится описание дорожки. Описание состоит из нескольких символов ‘a’ и ‘b’: ‘a’ обозначает батут для прыжка в длину, а ‘b’ — в высоту. Батуты перечислены слева направо вдоль направления дорожки. Общее число батутов не превосходит 75 000. На дорожке есть хотя бы один батут.
Выведите одно число — искомое число способов пройти игру.
abab
3
В примере из условия есть три варианта пройти игру:
- первый прыжок в длину на первом батуте, второй прыжок — на втором батуте;
- первый прыжок в длину на первом батуте, второй прыжок — на четвёртом батуте;
- первый прыжок в длину на третьем батуте, второй прыжок — на четвёртом батуте.