Название одной маленькой, но очень гордой корпорации состоит из n строчных английских букв. Корпорация решила провести ребрендинг — активную маркетинговую стратегию, включающую комплекс мероприятий по изменению бренда (как компании, так и производимого ею товара), либо его составляющих: названия, логотипа, слогана. Начать решили именно с названия.
Для этого корпорация последовательно наняла \(m\) дизайнеров. Как только компания нанимает \(i\)-го дизайнера, тот сразу вносит свою лепту в создание нового имени корпорации следующим образом: он меняет в текущей версии названия все буквы \(x_i\) на \(y_i\) , а все буквы \(y_i\) на \(x_i\), после чего получается новая версия. Возможно, каких-то из этих букв в строке нет, а также возможно, что \(x_i\) совпадает с \(y_i\). Вариант имени, получившийся после работы последнего дизайнера, становится новым названием корпорации.
Менеджер Аркадий лишь недавно устроился на работу в эту фирму, но уже проникся корпоративным духом и очень переживает за успех ребрендинга. Естественно, ему не терпится узнать, какое имя в итоге получит корпорация.
Удовлетворите любопытство Аркадия — назовите ему окончательный вариант названия.
В первой строке входных данных находятся два числа \(n\) и \(m (1 ⩽ n, m ⩽ 200 000)\) — длина изначального названия и количество нанятых дизайнеров соответственно.
Вторая строка состоит из n строчных английских букв и представляет собой изначальное имя корпорации.
В следующих \(m\) строках содержатся описания действий дизайнеров: в \(i\)-й из последующих строк записаны две строчные английские буквы \(x_i\) и \(y_i\).
Выведите окончательный вариант названия корпорации.
Во втором примере название корпорации последовательно претерпевает следующие изменения:
abacabadaba → babcbabdbab
babcbabdbab → cacbcacdcac
cacbcacdcac → cdcbcdcacdc
cdcbcdcacdc → cdcbcdcacdc
cdcbcdcacdc → cdcbcdcfcdc
cdcbcdcfcdc → cdcbcdcfcdc
6 1 police p m
molice
11 6 abacabadaba a b b c a d e g f a b b
cdcbcdcfcdc
Лесничий Хогвартса Хагрид собирается заняться разведением драконов, для этого он намерен закупить партию драконьих яиц. С этой целью он отправился в волшебный зоомагазин в Косом переулке.
Хагриду известно, что магическая сила новорождённого дракона зависит от веса яйца дракона в фунтах, а именно, она равняется сумме квадратов цифр в десятичной записи веса. Заметим, что в волшебном мире вес яйца дракона всегда выражается целым положительным числом фунтов.
Естественно, Хагрид желает завести себе драконов как можно большей суммарной силы, но его мотоцикл не сможет поднять груз весом более l фунтов. Ассортимент в волшебном зоомагазине поистине волшебный, поэтому можно считать, что для любого целого положительного веса x , Хагрид может купить в магазине произвольное количество яиц драконов с таким весом.
Напишите программу, которая определит максимальную возможную суммарную волшебную силу драконов, родившихся из яиц, которые Хагрид сможет увезти на своём мотоцикле.
В единственной строке входных данных находится целое число l ( 1 ≤ l ≤ 10 12 ) — максимальный вес груза, который может поднять мотоцикл Хагрида.
Выведите единственное целое число — максимальную возможную суммарную волшебную силу драконов, которых Хагрид будет разводить рядом с Хогвартсом, при условии, что он съездит за яйцами только один раз и увезёт всю покупку на своём мотоцикле.
В первом примере выгоднее всего купить одно яйцо весом 6 фунтов.
Во втором примере выгоднее всего купить два яйца весом 9 фунтов каждое.
6
36
18
162
Команда пушистых спасателей сидела без дела в своём дупле, когда неожиданно поступил сигнал бедствия. В считанные мгновения все были на своих местах, и дирижабль бурундучков-спасателей отправился в путь.
Будем считать, что действие происходит на декартовой плоскости. База спасателей расположена в точке ( x 1 , y 1 ) , а сигнал бедствия поступил из точки ( x 2 , y 2 ) .
Благодаря инженерному искусству Гаечки, летательный аппарат спасателей может произвольное количество раз в любые моменты времени мгновенно изменить свою текущую скорость и направление движения. Единственное ограничение — величина скорости дирижабля относительно воздуха не может превосходить
 метров в секунду.
метров в секунду.
Разумеется, как настоящий спасатель, Гаечка хочет лететь так, чтобы оказаться на месте происшествия как можно быстрее. Дело осложняется тем, что в небе дует ветер, который влияет на перемещение дирижабля. Согласно прогнозу погоды, в ближайшие
t
секунд скорость ветра будет характеризоваться вектором
(
v
x
,
v
y
)
, а по прошествии
t
секунд скорость ветра станет равна
(
w
x
,
w
y
)
. Данные вектора определяют как направление ветра, так и его скорость. Формально, если дирижабль находится в точке
(
x
,
y
)
, его собственная скорость относительно воздуха равна нулю и при этом дует ветер
(
u
x
,
u
y
)
, то для любого неотрицательного вещественного числа
 , через
, через
 секунд дирижабль окажется в точке с координатами
секунд дирижабль окажется в точке с координатами
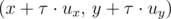 .
.
Гаечка занята управлением дирижаблем, поэтому она попросила Чипа вычислить, как скоро они смогут быть на месте, с чем он легко справился. Однако Дейл убеждён, что Чип не справился вычислить ответ и назвал случайное значение, лишь бы не ударить в грязь лицом перед Гаечкой. Чтобы пристыдить Чипа, Дейл попросил вас посчитать правильный ответ.
Гарантируется, что скорость ветра в любой момент времени строго меньше максимально возможной скорости дирижабля относительно воздуха.
В первой строке ввода записаны четыре целых числа x 1 , y 1 , x 2 , y 2 ( | x 1 |, | y 1 |, | x 2 |, | y 2 | ≤ 10 000 ) — координаты дупла спасателей и точки, из которой поступил сигнал бедствия.
Во второй строке записаны два целых числа
 и
t
(
0 <
v
,
t
≤ 1000
), задающих соответственно максимальную скорость дирижабля бурундуков и момент времени, в который произойдёт перемена ветра, согласно прогнозу погоды.
и
t
(
0 <
v
,
t
≤ 1000
), задающих соответственно максимальную скорость дирижабля бурундуков и момент времени, в который произойдёт перемена ветра, согласно прогнозу погоды.
Далее, по одной в строке записаны две пары целых чисел
(
v
x
,
v
y
)
и
(
w
x
,
w
y
)
, описывающие ветер в первые
t
секунд и ветер, который будет дуть всё остальное время, соответственно. Гарантируется, что
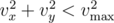 и
и
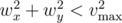 .
.
Выведите единственное число — минимальное время, через которое спасатели смогут оказаться в точке ( x 2 , y 2 ) . Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6 .
А именно: пусть ваш ответ равен
a
, а ответ жюри —
b
. Проверяющая программа будет считать ваш ответ правильным, если
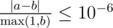 .
.
0 0 5 5 3 2 -1 -1 -1 0
3.729935587093555327
Гарри Поттер и Тот-Кого-Нельзя-Называть снова сошлись в смертельном поединке. На этот раз они стоят в противоположных концах коридора длины l метров и одновременно пускают в противника свои смертельные заклинания. Известно, что магический импульс заклинания Гарри распространялся со скоростью p метров в секунду, а магический импульс заклинания Сами-Знаете-Кого — со скоростью q метров в секунду.
Импульсы движутся по коридору навстречу друг другу, и в момент столкновения разворачиваются и летят обратно к тем, кто их выпустил, не меняя своих изначальных скоростей. Затем, каждый из волшебников отражает вернувшийся импульс и тот снова летит в сторону врага, опять же не меняя своей скорости.
Так как Гарри отлично освоил основы магии, то он знает, что после второго столкновения импульсы исчезнут, а в месте их встречи произойдёт сильный взрыв. Но вот с математикой у юного волшебника проблемы, поэтому он просит вас вычислить расстояние от его позиции до места второй встречи импульсов заклинаний, при условии, что противники стоят на месте в течение всего боя.
В первой строке ввода записано единственное целое число l ( 1 ≤ l ≤ 1 000 ) — длина коридора, в котором происходит поединок.
Во второй строке находится целое число p , в третьей целое число q ( 1 ≤ p , q ≤ 500 ) — скорости магических импульсов Гарри Поттера и Того-Кого-Нельзя-Называть соответственно.
Выведите единственное число — расстояние от конца коридора, в котором стоит Гарри, до места второй встречи импульсов заклинаний. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 4 .
А именно: пусть ваш ответ равен
a
, а ответ жюри —
b
. Проверяющая программа будет считать ваш ответ правильным, если
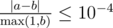 .
.
В первом тесте из условия скорости импульсов равны, поэтому обе их встречи произойдут ровно посередине между Гарри и Тем-Кого-Нельзя-Называть.
100 50 50
50
199 60 40
119.4
Опасаясь приближения мирового экономического кризиса, государства Бермания, Беранция и Берталия заключили союз и разрешили жителям всех входящих в него государств беспрепятственный проход по территории любого из них. Дополнительно было решено построить дороги между государствами так, чтобы из любой точки любого государства можно было добраться до любой точки любого другого государства.
Так как дороги всегда обходятся недёшево, правительства государств новообразованного союза попросили вас помочь им оценить затраты. Для этого вам была выдана карта, которая представляет собой клетчатый прямоугольник из n строк по m клеток в каждой. Любая клетка карты либо принадлежит одному из трёх государств, либо является областью, на которой можно построить дорогу, либо является областью, на которой дорогу построить нельзя. Проходимыми являются все клетки, принадлежащие государствам, а также все клетки, в которых построены дороги. Из любой проходимой клетки можно перемещаться вверх, вниз, вправо и влево, если соответствующая такому перемещению клетка существует и является проходимой.
Требуется построить дороги в минимальном количестве клеток так, чтобы стало возможным добраться из любой клетки любого государства до любой клетки любого другого государства.
Гарантируется, что изначально из любой клетки любого государства можно добраться до любой клетки этого же государства, перемещаясь только по его клеткам. Также гарантируется, что на карте присутствует хотя бы одна клетка каждого государства.
В первой строке ввода записаны размеры карты n и m ( 1 ≤ n , m ≤ 1000 ) — количество строк и столбцов соответственно.
Следующие n строк содержат по m символов каждая и описывают строки карты. Цифры от 1 до 3 означают принадлежность соответствующему государству. Символ ' . ' соответствует клетке, на которой можно построить дорогу, а символ ' # ' соответствует клетке, на которой дорогу построить нельзя.
Выведите единственное целое число — минимальное количество клеток, в которых необходимо построить дороги, чтобы соединить все клетки всех государств. Если это сделать невозможно, то выведите -1 .
4 5 11..2 #..22 #.323 .#333
2
1 5 1#2#3
-1