Темы
Информатика(2656 задач)
--->
228 задач
<---
#113357
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2015,
Лига Б,
Задача I
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
На планете Бублик идёт война. Каждый из городов планеты принадлежит одному из нескольких враждующих государств. На планете есть n городов, расположенных вокруг дырки от Бублика и пронумерованных числами от 1 до n в порядке их обхода по кругу. Расстояние между любыми двумя соседними по кругу городами (в том числе между городом номер n и городом номер 1 ) одно и то же, а именно 42 бубликанских километра.
Когда на какой-то город происходит нападение, из него в противоположных направлениях выбегают два гонца. Двигаясь с одинаковой постоянной скоростью, они пробегают полный круг, предупреждая о нападении все города этого государства на своём пути. Чем больше максимальное время, которое пройдёт между нападением на какой-то город государства и моментом, когда все города этого государства будут оповещены о нападении, тем более уязвимым является данное государство. Вы решили выбрать наиболее уязвимое государство и предупредить его об опасности.
Вам дана политическая карта планеты Бублик. Требуется найти два города, принадлежащих одному государству, расстояние между которыми максимально.
Входные данные
В первой строке содержится единственное число n ( 2 ≤ n ≤ 1000 ) — количество городов.
Во второй строке содержатся n чисел, i -е из которых — номер государства, владеющего i -м городом. Номера всех государств — целые числа от 1 до 10 9 включительно.
Гарантируется, что найдутся хотя бы два города, принадлежащие одному государству.
Выходные данные
Выведите номера двух различных городов, принадлежащих одному государству, расстояние между которыми максимально. Если правильных ответов несколько, разрешается вывести любой из них.
Примечание
В первом примере первый и четвёртый города принадлежат государству 1 , а расстояние между ними составляет 126 бубликанских километров, тогда как расстояния между городами 3 и 5 и городами 2 и 6 составляют 84 бубликанских километра.
Во втором примере расстояние между вторым и шестым городом равно 126 бубликанских километров.
Примеры
Входные данные
7 1 2 3 1 3 10 2
Выходные данные
1 4
Входные данные
7 30 40 10 40 10 40 20
Выходные данные
2 6
#113358
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2015,
Лига А,
Задача A
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
По рзеульаттам илссеовадний одонго анлигйсокго унвиертисета, не иеемт занчнеия, в кокам пряокде рсапожолены бкувы в солве. Галвоне, чотбы преавя и пслоендяя бквуы блыи на мсете. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, все рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы чиатем не кдаужю бкуву по отдльенотси, а все солво цликеом.
Смогли прочитать текст выше? Теперь, руководствуясь описанными ниже правилами, напишите программу, которая моделирует чтение человеком текста.
Пусть человеку известен набор из n слов языка. Будем считать, что человек может прочитать слово s , если в его словаре имеется хотя бы одно такое слово w , что выполнены два условия:
- Существует способ переставить буквы слова w так, чтобы получилось слово s .
- Слова w и s начинаются с одной и той же буквы, а также заканчиваются одной и той же буквой.
Вам дан набор известных человеку слов и некоторый текст. Определите, сколько слов из текста человек не сможет прочитать в соответствии с данным выше определением. Каждое слово должно учитываться в ответ столько раз, сколько раз оно встречается в тексте.
Входные данные
В первой строке входных данных содержится число n ( 1 ≤ n ≤ 100 000 ) — количество слов, известных человеку. Cледующие n строк содержат эти слова по одному в строке. Суммарная длина всех слов не превышает 100 000 символов. Слова в словаре могут повторяться.
В следующей строке содержится число m ( 1 ≤ m ≤ 100 000 ) — количество слов в тексте. В последней строке входных данных содержится текст, который представляет собой набор слов, разделенных пробелами. Суммарная длина всех слов в тексте не превышает 100 000 символов. Слова в тексте могут повторяться.
Каждое слово во входных данных представляет собой непустую последовательность строчных английских букв.
Выходные данные
В единственной строке выведите количество слов текста, которые человек не сможет прочитать.
Примеры
Входные данные
3 moscow command olympiad 3 mcsoow cmaonmd oalympid
Выходные данные
0
Входные данные
2 british scientist 3 brrtish brrtish scientist
Выходные данные
2
#113359
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2015,
Лига А,
Задача B
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Школьник Вася очень любит читать книжки по программированию и математике. Недавно он прочёл в энциклопедии статью, в которой рассказывалось о методе медианного сглаживания и его многочисленных применениях в науке и технике. Идея метода Васе очень понравилась, и он решил опробовать его на практике.
При использовании простейшего варианта медианного сглаживания по последовательности чисел a 1 , a 2 , ..., a n строится новая последовательность чисел b 1 , b 2 , ..., b n по следующему алгоритму:
- b 1 = a 1 , b n = a n , то есть первое и последнее число новой последовательности совпадают с соответствующими числами исходной последовательности.
- При i = 2, ..., n - 1 значение b i полагается равным медиане трёх значений a i - 1 , a i и a i + 1 .
Напомним, что медианой набора из трех чисел называется число, которое окажется на втором месте, если три числа выписать в порядке неубывания. Например, медианой набора 5, 1, 2 является число 2, а медианой набора 1, 0, 1 — число 1.
Чтобы не усложнять себе задачу, Вася решил применять метод только к последовательностям, состоящим из нулей и единиц.
Проделав нехитрую процедуру один раз, Вася посмотрел на получившуюся последовательность и подумал: что будет, если снова применить к ней алгоритм, а потом применить его к следующему результату и так далее? Рассмотрев пару примеров, Вася обнаружил, что через несколько применений медианного сглаживания последовательность может перестать изменяться. Будем говорить, что последовательность стабильна , если она не изменяется при применении к ней медианного сглаживания.
Васе стало интересно, всегда ли последовательность рано или поздно становится стабильной. Он просит вас написать программу, которая по заданной последовательности нулей и единиц определит, становится ли она когда-нибудь стабильной, и если да, то сколько раз для этого нужно применить к ней метод медианного сглаживания.
Входные данные
В первой строке входных данных находится одно целое число n ( 3 ≤ n ≤ 500 000 ) — число элементов в рассматриваемой последовательности.
В следующей строке находится исходная последовательность чисел a 1 , a 2 , ..., a n , состоящая только из нулей и единиц.
Выходные данные
В случае, если последовательность никогда не станет стабильной, выведите одно число - 1 .
В противном случае в первой строке выведите одно число — минимальное число раз, которое нужно применить алгоритм медианного сглаживания, прежде чем последовательность станет стабильной. Во второй строке выведите n чисел через пробел — саму итоговую последовательность.
Примечание
Во втором примере стабилизация наступает через два шага:
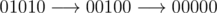, а последовательность
00000
, как нетрудно заметить, является стабильной.
Примеры
Входные данные
4 0 0 1 1
Выходные данные
0 0 0 1 1
Входные данные
5 0 1 0 1 0
Выходные данные
2 0 0 0 0 0
#113360
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2015,
Лига А,
Задача C
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Как вам, может быть, известно, на одном хлебобулочном заводе, который специализируется на производстве багетов, всем заправляет вовсе не гендиректор, а его жена, хотя официально она даже не является сотрудницей завода. Однажды об этом узнал и сам гендиректор. Он страшно разозлися и решил показать жене, кто на заводе хозяин. Для этого он предложил ей сыграть в управленческую игру.
Иерархия сотрудников завода описывается следующими простыми правилами:
- Всего на заводе n + 1 сотрудник. У каждого из них, кроме гендиректора, есть непосредственный начальник — один из других сотрудников. У гендиректора начальника нет.
- Все сотрудники завода так или иначе подчинены гендиректору, то есть любой сотрудник является либо гендиректором, либо непосредственным подчинённым гендиректора, либо непосредственным подчинённым непосредственного подчинённого гендиректора и так далее.
Гендиректор и его жена ходят по очереди, начинает гендиректор. За один ход необходимо выбрать одного произвольного сотрудника, чьим непосредственным начальником ещё не является гендиректор, и исправить эту оплошность, то есть назначить гендиректора непосредственным начальником выбранного сотрудника. Тот, кто не может сделать ход, проигрывает.
Определите, кто из супругов выиграет при правильной игре и сможет называть себя настоящим хозяином завода.
Входные данные
В первой строке находится число n ( 1 ≤ n ≤ 200 000 ) — количество сотрудников на хлебобулочном заводе, не считая директора .
Во второй строке следуют числа d 1 , d 2 , ..., d n ( 0 ≤ d i < i ), где d i означает номер сотрудника, который является непосредственным начальником сотрудника под номером i . Сам гендиректор имеет номер 0 .
Выходные данные
Если при правильной игре выигрывает гендиректор, то выведите « Husband » (без кавычек). Если, как бы ни старался гендиректор, победу в игре одержит его жена, то выведите « Wife » (без кавычек).
Примечание
Во первом примере все сотрудники уже являются непосредственными подчинёнными гендиректора, поэтому в игре нельзя сделать ни одного хода.
Примеры
Входные данные
2 0 0
Выходные данные
Wife
Входные данные
6 0 1 2 1 4 5
Выходные данные
Husband
#113361
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2015,
Лига А,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Условие пока не опубликовано...
Примеры
Входные данные
6 1 police p m
Выходные данные
molice
Входные данные
11 6 abacabadaba a b b c a d e g f a b b
Выходные данные
cdcbcdcfcdc
Выбрано
:
|