Трамвайная линия имеет вид прямой. Петя живет в N трамвайных остановках от метро. Метро находится у нулевой остановки, в точке с координатой 0.
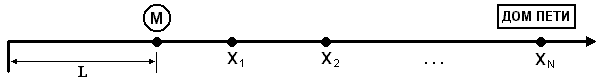
Выходя из метро, Петя хочет попасть домой как можно быстрее, но он очень не любит ждать трамвай на остановке. Поэтому, если, подходя к очередной трамвайной остановке, он не видит трамвая, то идет пешком вдоль трамвайной линии. Если в какой-то момент Петя видит трамвай, то он может принять решение вернуться на остановку, или продолжить свое движение к следующей остановке. Петя идет со скоростью U, трамвай едет со скоростью V. Нужно найти минимальное расстояние L, которое должно просматриваться перед нулевой остановкой, чтобы он мог идти со своей скоростью в сторону дома, не опасаясь, что трамвай его обгонит между остановками.
Во входном файле находятся три числа N, U и V (N ≤ 1000, U и V – положительные вещественные), за которым будет следовать N вещественных чисел – X1, X2,... Xn (0 < X1 < X2 < … < Xn < 106), разделенных пробелами.
В выходной файл ваша программа должна вывести число L с точностью до 10-4.
1 1 10 2
9.0000
Компания MacroHard разработала новый язык программирования PASCAL++. В этом языке имеется оператор вывода PrintLn, с помощью которого можно выводить строки любой длины. По стандарту языка, разработанному специалистами компании, некоторые комбинации символов в строке должны при выводе играть особую роль:
| Комбинация | Значение |
| \n | Переход на новую строку |
| \t | Вывод K пробелов (\(1\leq K \leq 7\))), после чего курсор оказывается на позиции, имеющей номер вида \(7N+1\) (первая позиция каждой строки имеет номер 1). |
| \\ | Вывод символа "\". |
| \XY где X и Y – шестнадцатеричные цифры (0..9, A..F или a..f), причем XY20 | Вывод символа, имеющего ASCII код XY |
Например, строка "New line\ntab\tslash\\\nA char \41, rus Б \81" должна была быть напечатана в следующем виде :
-
Напечатано
Здесь пробелы для наглядности обозначены символами
New line
tab slash\
A char A, rus Б Б
Newline
tabslash\
AcharA,rusББ
К сожалению, главный программист забыл добавить в компилятор правильную процедуру форматирования. Поэтому строки выводятся прямо так, как они были записаны. Ваша задача состоит в том, чтобы преобразовать файл, полученный в результате выполнения одного или нескольких операторов PrintLn к форме, которая была задумана.
Входной файл содержит одну или несколько строк, каждая из которых является результатом работы неправильного оператора PrintLn. Размер файла не превышает 100000 байт.
(Все символы "\", встречающиеся во входном файле участвуют в создании какой-либо ключевой комбинации, т.е. сразу после любой последовательности, состоящей из нечетного количества подряд идущих символов "\", следует символ из набора {"n", "t", "\", "0".."9", "A".."F", "a".."f" }, причем в случае символа из множества {"0".."9", A".."F", "a".."f"}, затем следует еще один символ из этого множества.)
Выведите в выходной файл, как выглядел бы данный текст, если бы он был перобразован по соответствующим правилам языка PASCAL++.
Примеры
| Входные данные | Выходные данные |
| New line\ntab\tslash\\ A char \41, rus Б \81 | New line tab slash\ A char A, rus Б Б |
Известно, что в книгах для слепых для обозначения различных букв используются различные комбинации выступов, которые читающий различает на ощупь. Пусть для обозначения буквы используется прямоугольник шириной M мм и высотой N мм, причем некоторые входящие в него квадратики размера 1∙1 содержат выступ.
Поскольку слепой не видит границ прямоугольника, то он не может различить комбинации, получающиеся друг из друга сдвигом. Так, он не может различить комбинации а) и б) на рисунке 1. (В то же время комбинации а) и в) являются различимыми, поскольку не могут быть получены друг из друга сдвигом)
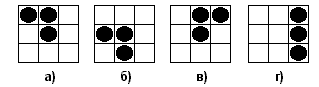
Рисунок 1.
Из-за этого при разработке алфавита для слепых появилась проблема: сколько различных букв можно представить с помощью выступов, если запрещается сопоставлять различным буквам комбинации, получающиеся друг из друга сдвигом. Прямоугольник совсем без выступов также нельзя использовать в качестве буквы (поскольку при написании слова между некоторыми буквами может появиться такой прямоугольник, например между а) и г) на рисунке 1).
Требуется подсчитать количество различных букв, которые можно представить таким способом, если прямоугольник имеет размер M∙N.
В качестве примера, все буквы размера 2∙2 приведены на рисунке 2. (Среди комбинаций, отвечающих одной букве, приведена только одна)

Рисунок 2.
Входной файл содержит числа M и N, разделенный пробелом. Поскольку человек одновременно не может воспринимать слишком много информации, M∙N ≤ 30.
Выведите в выходной файл единственное число – количество различных букв, которые слепой сможет различить при заданном размере прямоугольника.
2 3
44
В новом учебном году на занятия в компьютерные классы Дворца Творчества Юных пришли учащиеся, которые были разбиты на N групп. В i-й группе оказалось Xi человек. Тут же перед директором встала серьезная проблема: как распределить группы по аудиториям. Во дворце имеется M ≥ N аудиторий, в j-й аудитории имеется Yj компьютеров. Для занятий необходимо, чтобы у каждого учащегося был компьютер и еще один компьютер был у преподавателя. Переносить компьютеры из одной аудитории в другую запрещается. Помогите директору!
Напишите программу, которая найдет, какое максимальное количество групп удастся одновременно распределить по аудиториям, чтобы всем учащимся в каждой группе хватило компьютеров, и при этом остался бы еще хотя бы один для учителя.
На первой строке входного файла расположены числа N и M (1 ≤ N ≤ M ≤ 1000). На второй строке расположено N чисел — X1 , …, XN(1 ≤ Xi ≤ 1000 для всех 1 ≤ i ≤ N). На третьей строке расположено M чисел Y1, ..., YM (1 ≤ Yi ≤ 1000 для всех 1 ≤ i ≤ M).
Выведите на первой строке число P - количество групп, которые удастся распределить по аудиториям. На второй строке выведите распределение групп по аудиториям – N чисел, i-е число должно соответствовать номеру аудитории, в которой должна заниматься i-я группа. (Нумерация как групп, так и аудиторий, начинается с 1). Если i-я группа осталась без аудитории, i-е число должно быть равно 0. Если допустимых распределений несколько, выведите любое из них.
3 3 1 2 3 3 4 2
3 3 1 2
Известно, что о создателе шахмат ходит множество легенд. Недавно в одной древней библиотеке была обнаружена еще одна. В ней утверждается, что когда создатель игры рассказал правителю о своем изобретении и попросил скромную награду, правитель сказал ему следующее:
Возьми шахматную доску и поставь на нее коня. На ту клетку, на которую ты поставишь коня, я положу 2K золотых монет. На те клетки, на которые ты сможешь дойти конем за 1 ход, я положу 2K-1 золотых монет. И вообще, если с клетки, на которую ты поставишь коня, ты сможешь дойти до некоторой клетки самое меньшее за P ≤ K ходов, я положу на нее 2K-P золотых монет. Но если ты проявишь чрезмерную жадность и не сможешь унести все монеты, которые я выложу на доску, то я прикажу отрубить тебе голову!
Ученым известно, что создатель шахмат был очень умным человеком. Он знал, что сможет унести не более M монет. Поэтому он поставил коня на такую клетку, чтобы получит как можно больше монет и остаться живым. Если же такой клетки не было, то он тихо покинул город. Помогите ученым узнать, сколько монет заработал создатель шахмат своим изобретением и на какую клетку он поставил коня.
Примечание
 Напоминаем, что шахматная доска имеет форму квадрата 8 на 8 клеток, столбцы называются латинскими буквами от a до h, а строки – цифрами от 1 до 8, клетка имеет название в виде пары буква-цифра, в зависимости от того, на пересечении какого столбца и какой строки она находится.
Напоминаем, что шахматная доска имеет форму квадрата 8 на 8 клеток, столбцы называются латинскими буквами от a до h, а строки – цифрами от 1 до 8, клетка имеет название в виде пары буква-цифра, в зависимости от того, на пересечении какого столбца и какой строки она находится.
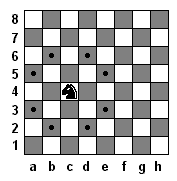
Конь ходит буквой "Г" – на 2 клетки в горизонтальном или вертикальном направлении и затем на одну клетку в перпендикулярном направлении. Разумеется, конь не может выходить за пределы доски.
Шахматная доска и возможные ходы коня в одной из позиций изображены на рисунке.
На первой строке находятся числа K (0 ≤ K ≤ 25) и M (1 ≤ M ≤ 109).
На первой строке выходного файла выведите число N - количество монет, которое получил создатель шахмат (Если ему не удалось заработать ни одной монеты, то N = 0). Если N > 0, на второй строке выведите в любом порядке, но без повторений, все возможные клетки, в которые он мог поставить коня. Разделяйте имена клеток пробелами.
1 7
6 a3 a4 a5 a6 b2 b7 c1 c8 d1 d8 e1 e8 f1 f8 g2 g7 h3 h4 h5 h6
1 10
10 c3 c4 c5 c6 d3 d4 d5 d6 e3 e4 e5 e6 f3 f4 f5 f6