Трамвайная линия имеет вид прямой. Петя живет в N трамвайных остановках от метро. Метро находится у нулевой остановки, в точке с координатой 0.

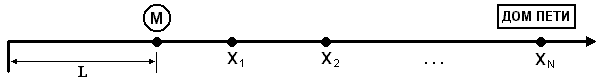
Выходя из метро, Петя хочет попасть домой как можно быстрее, но он очень не любит ждать трамвай на остановке. Поэтому, если, подходя к очередной трамвайной остановке, он не видит трамвая, то идет пешком вдоль трамвайной линии. Если в какой-то момент Петя видит трамвай, то он может принять решение вернуться на остановку, или продолжить свое движение к следующей остановке. Петя идет со скоростью U, трамвай едет со скоростью V. Нужно найти минимальное расстояние L, которое должно просматриваться перед нулевой остановкой, чтобы он мог идти со своей скоростью в сторону дома, не опасаясь, что трамвай его обгонит между остановками.

Недавно один известный художник-абстракционист произвел на свет новый шедевр – картину «Два черных непересекающихся прямоугольника». Картина представляет собой прямоугольник \(m\)×\(n\), разбитый на квадраты 1×1, некоторые из которых закрашены любимым цветом автора – черным. Федя – не любитель абстрактных картин, однако ему стало интересно, действительно ли на картине изображены два непересекающихся прямоугольника. Помогите ему это узнать. Прямоугольники не пересекаются в том смысле, что они не имеют общих клеток.

Рассмотрим последовательность из открывающихся и закрывающихся круглых скобок. Последовательность называется правильной, если она может быть построена по следующим правилам:

1. пустая строка является правильной скобочной последовательностью; 2. если S – правильная скобочная последовательность, то (S) – тоже правильная скобочная последовательность. 3. если A и B – правильные скобочные последовательности, то AB – тоже правильная скобочная последовательность.

Примеры правильных скобочных последовательностей – «», «()», «((()))», «()()()», «((()())())(())». Неформально говоря, правильная скобочная последовательность – это последовательность скобок, которая может быть получена из некоторого арифметического выражения удалением из него всего, кроме скобок.

Рассмотрим последовательность скобок, содержащую как круглые, так и квадратные скобки. Пусть разрешается выполнять следующие операции: заменить открывающуюся квадратную скобку на произвольное число открывающихся круглых и заменить закрывающуюся квадратную скобку на произвольное количество закрывающихся круглых. Разрешается при замене создавать ноль скобок, то есть просто удалять соответствующую квадратную скобку.

Требуется с использованием указанных операций получить из заданной строки минимальную по длине правильную скобочную последовательность, состоящую только из круглых скобок.

Например, из строки [)())(]()] можно получить правильную скобочную последовательность (()())()().