Известно, что в книгах для слепых для обозначения различных букв используются различные комбинации выступов, которые читающий различает на ощупь. Пусть для обозначения буквы используется прямоугольник шириной M мм и высотой N мм, причем некоторые входящие в него квадратики размера 1∙1 содержат выступ.
Поскольку слепой не видит границ прямоугольника, то он не может различить комбинации, получающиеся друг из друга сдвигом. Так, он не может различить комбинации а) и б) на рисунке 1. (В то же время комбинации а) и в) являются различимыми, поскольку не могут быть получены друг из друга сдвигом)
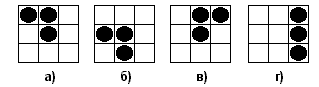
Рисунок 1.
Из-за этого при разработке алфавита для слепых появилась проблема: сколько различных букв можно представить с помощью выступов, если запрещается сопоставлять различным буквам комбинации, получающиеся друг из друга сдвигом. Прямоугольник совсем без выступов также нельзя использовать в качестве буквы (поскольку при написании слова между некоторыми буквами может появиться такой прямоугольник, например между а) и г) на рисунке 1).
Требуется подсчитать количество различных букв, которые можно представить таким способом, если прямоугольник имеет размер M∙N.
В качестве примера, все буквы размера 2∙2 приведены на рисунке 2. (Среди комбинаций, отвечающих одной букве, приведена только одна)

Рисунок 2.
Входной файл содержит числа M и N, разделенный пробелом. Поскольку человек одновременно не может воспринимать слишком много информации, M∙N ≤ 30.
Выведите в выходной файл единственное число – количество различных букв, которые слепой сможет различить при заданном размере прямоугольника.
2 3
44
В новом учебном году на занятия в компьютерные классы Дворца Творчества Юных пришли учащиеся, которые были разбиты на N групп. В i-й группе оказалось Xi человек. Тут же перед директором встала серьезная проблема: как распределить группы по аудиториям. Во дворце имеется M ≥ N аудиторий, в j-й аудитории имеется Yj компьютеров. Для занятий необходимо, чтобы у каждого учащегося был компьютер и еще один компьютер был у преподавателя. Переносить компьютеры из одной аудитории в другую запрещается. Помогите директору!
Напишите программу, которая найдет, какое максимальное количество групп удастся одновременно распределить по аудиториям, чтобы всем учащимся в каждой группе хватило компьютеров, и при этом остался бы еще хотя бы один для учителя.
На первой строке входного файла расположены числа N и M (1 ≤ N ≤ M ≤ 1000). На второй строке расположено N чисел — X1 , …, XN(1 ≤ Xi ≤ 1000 для всех 1 ≤ i ≤ N). На третьей строке расположено M чисел Y1, ..., YM (1 ≤ Yi ≤ 1000 для всех 1 ≤ i ≤ M).
Выведите на первой строке число P - количество групп, которые удастся распределить по аудиториям. На второй строке выведите распределение групп по аудиториям – N чисел, i-е число должно соответствовать номеру аудитории, в которой должна заниматься i-я группа. (Нумерация как групп, так и аудиторий, начинается с 1). Если i-я группа осталась без аудитории, i-е число должно быть равно 0. Если допустимых распределений несколько, выведите любое из них.
3 3 1 2 3 3 4 2
3 3 1 2
Известно, что о создателе шахмат ходит множество легенд. Недавно в одной древней библиотеке была обнаружена еще одна. В ней утверждается, что когда создатель игры рассказал правителю о своем изобретении и попросил скромную награду, правитель сказал ему следующее:
Возьми шахматную доску и поставь на нее коня. На ту клетку, на которую ты поставишь коня, я положу 2K золотых монет. На те клетки, на которые ты сможешь дойти конем за 1 ход, я положу 2K-1 золотых монет. И вообще, если с клетки, на которую ты поставишь коня, ты сможешь дойти до некоторой клетки самое меньшее за P ≤ K ходов, я положу на нее 2K-P золотых монет. Но если ты проявишь чрезмерную жадность и не сможешь унести все монеты, которые я выложу на доску, то я прикажу отрубить тебе голову!
Ученым известно, что создатель шахмат был очень умным человеком. Он знал, что сможет унести не более M монет. Поэтому он поставил коня на такую клетку, чтобы получит как можно больше монет и остаться живым. Если же такой клетки не было, то он тихо покинул город. Помогите ученым узнать, сколько монет заработал создатель шахмат своим изобретением и на какую клетку он поставил коня.
Примечание
 Напоминаем, что шахматная доска имеет форму квадрата 8 на 8 клеток, столбцы называются латинскими буквами от a до h, а строки – цифрами от 1 до 8, клетка имеет название в виде пары буква-цифра, в зависимости от того, на пересечении какого столбца и какой строки она находится.
Напоминаем, что шахматная доска имеет форму квадрата 8 на 8 клеток, столбцы называются латинскими буквами от a до h, а строки – цифрами от 1 до 8, клетка имеет название в виде пары буква-цифра, в зависимости от того, на пересечении какого столбца и какой строки она находится.
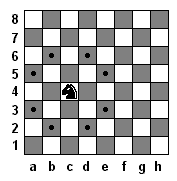
Конь ходит буквой "Г" – на 2 клетки в горизонтальном или вертикальном направлении и затем на одну клетку в перпендикулярном направлении. Разумеется, конь не может выходить за пределы доски.
Шахматная доска и возможные ходы коня в одной из позиций изображены на рисунке.
На первой строке находятся числа K (0 ≤ K ≤ 25) и M (1 ≤ M ≤ 109).
На первой строке выходного файла выведите число N - количество монет, которое получил создатель шахмат (Если ему не удалось заработать ни одной монеты, то N = 0). Если N > 0, на второй строке выведите в любом порядке, но без повторений, все возможные клетки, в которые он мог поставить коня. Разделяйте имена клеток пробелами.
1 7
6 a3 a4 a5 a6 b2 b7 c1 c8 d1 d8 e1 e8 f1 f8 g2 g7 h3 h4 h5 h6
1 10
10 c3 c4 c5 c6 d3 d4 d5 d6 e3 e4 e5 e6 f3 f4 f5 f6
 Правительство страны Ректилании решило построить новый город. По плану правительства, город должен быть построен на сетке M на N прямоугольных участков, размером 100 на 100 метров. Все улицы должны иметь ширину 100 метров и занимать соответственно одну горизонталь или вертикаль сетки. Вертикальные улицы должны пролегать по вертикалям с номерами X1...XV, горизонтальные – по горизонталям с номерами Y1...YH. При этом улицы не соприкасаются, то есть не бывает Xi = Xi-1 + 1 и соответственно Yj = Yj-1 + 1 .
Правительство страны Ректилании решило построить новый город. По плану правительства, город должен быть построен на сетке M на N прямоугольных участков, размером 100 на 100 метров. Все улицы должны иметь ширину 100 метров и занимать соответственно одну горизонталь или вертикаль сетки. Вертикальные улицы должны пролегать по вертикалям с номерами X1...XV, горизонтальные – по горизонталям с номерами Y1...YH. При этом улицы не соприкасаются, то есть не бывает Xi = Xi-1 + 1 и соответственно Yj = Yj-1 + 1 .
Все дома в новом городе должны занимать одну клетку сетки. Причем все дома должны находиться рядом с улицами, а в клетках, не имеющих общих сторон с улицами, будет разбит парк. Кроме того, дома не должны находиться на наружной стороне крайних улиц. Рисунок 1 изображает план города, рассмотренного в примере.
Теперь правительство Ректилании хочет знать, сколько домов будет построено в новом городе и сколько в нем будет клеток парка. Ваша задача состоит в том, чтобы написать программу, которая рассчитает эти величины.
На первой строке входного файла находятся числа M, N, V и H. (2 ≤ V < M ≤ 1000, 2 ≤ H < N ≤ 1000). На второй строке находятся координаты вертикальных улиц — V чисел: 1 = X1 < X2 < … < XV = M. На третьей строке находятся координаты горизонтальных улиц — H чисел 1 = Y1 < Y2 < … < YH = N. Все числа в строках разделены пробелами.
Выведите в выходной файл три числа: A – количество домов в новом городе, B — количество клеток, в которых будет разбит парк и C — количество клеток, по которым будут пролегать улицы. Разделяйте числа пробелами.
4 4 2 2 1 4 1 4
4 0 12
Клуб Юных Хакеров разработал новый язык для web-страниц. В этом языке у тегов нет атрибутов, и запрещается использовать пробелы в написании тега. А именно: назовем открывающим тегом языка HTHL (Hyper Text Hackers' Language) следующую последовательность:
"<", имя тега, ">"
а закрывающим тегом последовательность
"</", имя тега, ">"
где имя тега – любая последовательность латинских букв и цифр, не длиннее 100 символов. Рассмотрим примеры тегов языка HTHL:
<b> <par> <hthl> <hacker2> <super>
</i> </hthl> </br> </hyper> </down>
При написании браузера для просмотра своих страниц, юные хакеры столкнулись с проблемой поиска слова на странице. Ведь некоторые теги (в примере - <b>, <i> и <u>) и соответствующие закрывающие теги (в примере - </b>, </i> и </u>) не разрывают слово. Например, при поиске слова hello комбинация h<b><i>el</i>l</b>o должна быть найдена. Ваша задача состоит в том, чтобы помочь юным хакерам в решении нелегкой проблемы поиска.
На первой строке входного файла находится число K (0 ≤ K ≤ 100) — количество имен тегов, которые не разрывают слово. Следующие K строк содержат имена этих тегов.
На следующей строке находится N — количество строк в странице HTHL, в которой следует осуществлять поиск (1 ≤ N ≤ 100). Следующие N строк содержат текст страницы, все строки не длиннее 250 символов.
Следующая строка содержит число M — количество запросов (1 ≤ M ≤ 100). Затем следует M строк — слова, поиск которых следует осуществить в документе. Словом является любая последовательность латинских букв и цифр не длиннее 250 символов.
Гарантируется, что страница HTHL является корректной, т.е. все символы "<", "/" и ">" используются только в тегах, все теги записаны корректно.
Различие между большими и маленькими буквами следует игнорировать.
Выведите в выходной файл M строк — для каждого слова выведите номер строки в странице, на которой оно впервые встречается, либо 0, если число не встречается на странице (Нумерация строк идет с 1).
0 1 this page is very simple 5 this page is very simple
1 1 1 1 1