Известно, что в книгах для слепых для обозначения различных букв используются различные комбинации выступов, которые читающий различает на ощупь. Пусть для обозначения буквы используется прямоугольник шириной M мм и высотой N мм, причем некоторые входящие в него квадратики размера 1∙1 содержат выступ.
Поскольку слепой не видит границ прямоугольника, то он не может различить комбинации, получающиеся друг из друга сдвигом. Так, он не может различить комбинации а) и б) на рисунке 1. (В то же время комбинации а) и в) являются различимыми, поскольку не могут быть получены друг из друга сдвигом)
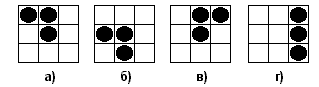
Рисунок 1.
Из-за этого при разработке алфавита для слепых появилась проблема: сколько различных букв можно представить с помощью выступов, если запрещается сопоставлять различным буквам комбинации, получающиеся друг из друга сдвигом. Прямоугольник совсем без выступов также нельзя использовать в качестве буквы (поскольку при написании слова между некоторыми буквами может появиться такой прямоугольник, например между а) и г) на рисунке 1).
Требуется подсчитать количество различных букв, которые можно представить таким способом, если прямоугольник имеет размер M∙N.
В качестве примера, все буквы размера 2∙2 приведены на рисунке 2. (Среди комбинаций, отвечающих одной букве, приведена только одна)
Рисунок 2.
Входной файл содержит числа M и N, разделенный пробелом. Поскольку человек одновременно не может воспринимать слишком много информации, M∙N ≤ 30.
Выведите в выходной файл единственное число – количество различных букв, которые слепой сможет различить при заданном размере прямоугольника.
2 3
44
В новом учебном году на занятия в компьютерные классы Дворца Творчества Юных пришли учащиеся, которые были разбиты на N групп. В i-й группе оказалось Xi человек. Тут же перед директором встала серьезная проблема: как распределить группы по аудиториям. Во дворце имеется M ≥ N аудиторий, в j-й аудитории имеется Yj компьютеров. Для занятий необходимо, чтобы у каждого учащегося был компьютер и еще один компьютер был у преподавателя. Переносить компьютеры из одной аудитории в другую запрещается. Помогите директору!
Напишите программу, которая найдет, какое максимальное количество групп удастся одновременно распределить по аудиториям, чтобы всем учащимся в каждой группе хватило компьютеров, и при этом остался бы еще хотя бы один для учителя.
На первой строке входного файла расположены числа N и M (1 ≤ N ≤ M ≤ 1000). На второй строке расположено N чисел — X1 , …, XN(1 ≤ Xi ≤ 1000 для всех 1 ≤ i ≤ N). На третьей строке расположено M чисел Y1, ..., YM (1 ≤ Yi ≤ 1000 для всех 1 ≤ i ≤ M).
Выведите на первой строке число P - количество групп, которые удастся распределить по аудиториям. На второй строке выведите распределение групп по аудиториям – N чисел, i-е число должно соответствовать номеру аудитории, в которой должна заниматься i-я группа. (Нумерация как групп, так и аудиторий, начинается с 1). Если i-я группа осталась без аудитории, i-е число должно быть равно 0. Если допустимых распределений несколько, выведите любое из них.
3 3 1 2 3 3 4 2
3 3 1 2
Правительство страны Ректилании решило построить новый город. По плану правительства, город должен быть построен на сетке M на N прямоугольных участков, размером 100 на 100 метров. Все улицы должны иметь ширину 100 метров и занимать соответственно одну горизонталь или вертикаль сетки. Вертикальные улицы должны пролегать по вертикалям с номерами X1...XV, горизонтальные – по горизонталям с номерами Y1...YH. При этом улицы не соприкасаются, то есть не бывает Xi = Xi-1 + 1 и соответственно Yj = Yj-1 + 1 .
Все дома в новом городе должны занимать одну клетку сетки. Причем все дома должны находиться рядом с улицами, а в клетках, не имеющих общих сторон с улицами, будет разбит парк. Кроме того, дома не должны находиться на наружной стороне крайних улиц. Рисунок 1 изображает план города, рассмотренного в примере.
Теперь правительство Ректилании хочет знать, сколько домов будет построено в новом городе и сколько в нем будет клеток парка. Ваша задача состоит в том, чтобы написать программу, которая рассчитает эти величины.
На первой строке входного файла находятся числа M, N, V и H. (2 ≤ V < M ≤ 1000, 2 ≤ H < N ≤ 1000). На второй строке находятся координаты вертикальных улиц — V чисел: 1 = X1 < X2 < … < XV = M. На третьей строке находятся координаты горизонтальных улиц — H чисел 1 = Y1 < Y2 < … < YH = N. Все числа в строках разделены пробелами.
Выведите в выходной файл три числа: A – количество домов в новом городе, B — количество клеток, в которых будет разбит парк и C — количество клеток, по которым будут пролегать улицы. Разделяйте числа пробелами.
4 4 2 2 1 4 1 4
4 0 12
Клуб Юных Хакеров разработал новый язык для web-страниц. В этом языке у тегов нет атрибутов, и запрещается использовать пробелы в написании тега. А именно: назовем открывающим тегом языка HTHL (Hyper Text Hackers' Language) следующую последовательность:
"<", имя тега, ">"
а закрывающим тегом последовательность
"</", имя тега, ">"
где имя тега – любая последовательность латинских букв и цифр, не длиннее 100 символов. Рассмотрим примеры тегов языка HTHL:
<b> <par> <hthl> <hacker2> <super>
</i> </hthl> </br> </hyper> </down>
При написании браузера для просмотра своих страниц, юные хакеры столкнулись с проблемой поиска слова на странице. Ведь некоторые теги (в примере - <b>, <i> и <u>) и соответствующие закрывающие теги (в примере - </b>, </i> и </u>) не разрывают слово. Например, при поиске слова hello комбинация h<b><i>el</i>l</b>o должна быть найдена. Ваша задача состоит в том, чтобы помочь юным хакерам в решении нелегкой проблемы поиска.
На первой строке входного файла находится число K (0 ≤ K ≤ 100) — количество имен тегов, которые не разрывают слово. Следующие K строк содержат имена этих тегов.
На следующей строке находится N — количество строк в странице HTHL, в которой следует осуществлять поиск (1 ≤ N ≤ 100). Следующие N строк содержат текст страницы, все строки не длиннее 250 символов.
Следующая строка содержит число M — количество запросов (1 ≤ M ≤ 100). Затем следует M строк — слова, поиск которых следует осуществить в документе. Словом является любая последовательность латинских букв и цифр не длиннее 250 символов.
Гарантируется, что страница HTHL является корректной, т.е. все символы "<", "/" и ">" используются только в тегах, все теги записаны корректно.
Различие между большими и маленькими буквами следует игнорировать.
Выведите в выходной файл M строк — для каждого слова выведите номер строки в странице, на которой оно впервые встречается, либо 0, если число не встречается на странице (Нумерация строк идет с 1).
0 1 this page is very simple 5 this page is very simple
1 1 1 1 1
Петя придумал новую игру. На стол кладется кучка из N спичек, и затем Петя с Ваней по очереди берут спички из кучки. Первым берет Петя, ему разрешается взять от 1 до K спичек. Затем игрок может взять любое количество спичек, не более чем на 1 превышающее то количество, которое взял игрок перед ним (можно взять меньше или столько же, но обязательно хотя бы одну). Например, если N = 10, K = 5, то на первом ходу Петя может взять 1, 2, 3, 4 или 5 спичек, если Петя возьмет 3, то на следующем ходу Ваня может взять 1, 2, 3 или 4, и если Ваня возьмет 1, то Петя затем может взять 1 или 2, и т. д. Проигрывает тот, кто возьмет последнюю спичку.
Теперь Петя хочет рассчитать какое количество спичек он должен взять на первом ходу, чтобы выиграть при любой игре Вани. Помогите ему.
На первой строке входного файла находятся числа N и K, разделенные пробелом. (1 ≤ K ≤ N ≤ 200).
Выведите в выходной файл все такие X, что, взяв на первом ходу X спичек, Петя выиграет. Если таких X не существует, выведите в выходной файл единственное число - 0. Числа следует разделять пробелами и выводить в порядке возрастания.
2 2
1
5 4
1 4