Темы
Информатика(2656 задач)
--->
8 задач
<---
#1382
Темы:
[Быстрая сортировка]
Источники:
[
Командные олимпиады,
Командные чемпионаты школьников Санкт-Петербурга по программированию,
2002,
Задача E
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
После пожара 1812 года на одной из главных улиц Москвы уцелел лишь один дом. Вернувшиеся после победы жители решили вновь поселиться на этой улице. При этом каждый решил построить себе дом такой же высоты, каким он был у него до пожара.
Дома будут строиться вплотную друг другу, а крыши соседних домов будут соединяться лестницами (длина лестницы равна разнице высот домов), чтобы трубочист мог путешествовать по крышам и чистить трубы.
Когда план постройки домов был уже почти утвержден, свое веское слово сказал Главный Трубочист. Он попросил построить дома так, чтобы суммарная длина лестниц была минимальной. Помогите ему составить такой план постройки домов.
Входные данные
Во входном файле записано сначала число N (1 ≤ N ≤ 10000), затем N чисел — высоты домов до пожара (это натуральные числа от 1 до 109), и затем K — номер уцелевшего дома.
Выходные данные
В выходной файл выведите высоты домов в таком порядке, чтобы выполнялось требование Главного Трубочиста. Обратите внимание, что K-ый дом (уцелевший) перестраивать не нужно (и следовательно его высота должна остаться прежней).
Примеры
Входные данные
5 1 3 4 2 6 2
Выходные данные
6 3 4 2 1
#1383
Источники:
[
Командные олимпиады,
Командные чемпионаты школьников Санкт-Петербурга по программированию,
2002,
Задача F
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
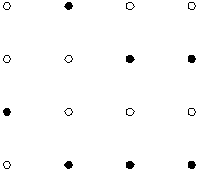
Рассмотрим целочисленную решетку размера N × N. Пусть некоторые ее узлы покрашены в белый, а некоторые – в черный цвет. Требуется определить количество квадратов на заданной решетке, то есть квадратов, вершины которых совпадают с узлами заданной решетки и покрашены в одинаковый цвет.
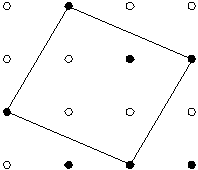
Например, на решетке размера 4 × 4, изображенной на рисунке 1 такой квадрат один, он показан на рисунке 2.
|
|
|
| Рисунок 1. Решетка 4 × 4. | Рисунок 2. Квадрат на решетке. |
Входные данные
Первая строка входного файла содержит число N – размер решетки (2 ≤ N ≤ 50). Следующие N строк содержат по N чисел из множества {0, 1} и задают решетку. Если точка с координатами (i, j) покрашена в белый цвет, то j-ое число i-ой строки есть 0, а если в черный, то 1.
Выходные данные
Выведите в выходной файл количество квадратов на решетке из входного файла.
Примеры
Входные данные
4 0 1 0 0 0 0 1 1 1 0 0 0 0 1 1 1
Выходные данные
1
#1384
Источники:
[
Командные олимпиады,
Командные чемпионаты школьников Санкт-Петербурга по программированию,
2002,
Задача H
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Группа альпинистов покорила много вершин и возвратилась в родной город. Одна из местных газет решила написать статью об их походе. Как выяснилось, в процессе похода альпинисты N раз останавливались на ночлег на той или иной высоте hi. Поскольку главный редактор газеты настаивает, чтобы название статьи было «Восхождение и спуск», решено было не упоминать о некоторых днях похода, рассказав лишь о 2k+1 дне, причем если статья будет рассказывать о x1-ом, x2-ом, …, x2k+1-ом (x1 < x2 < … < x2k+1)) дне, то должно выполняться условие hx1 < hx2 < … < hxk < hxk+1 > hxk+2 > … > hx2k+1 . Найдите максимальное k, для которого можно соответствующим образом выбрать 2k+1 день.
Входные данные
Первая строка входного файла содержит число N – количество дней в походе (1 ≤ N ≤ 100). Следующая строка содержит N целых чисел – h1, h2, …, hN (0 ≤ hi ≤ 104).
Выходные данные
В первой строке выходного файла выведите число k. Затем выведите 2k+1 число - номера дней, репортаж о которых следует включить в статью, в возрастающем порядке. Если возможных ответов несколько, выведите любой.
Примеры
Входные данные
7 0 3 1 10 7 2 1
Выходные данные
2 1 2 5 6 7
Входные данные
4 1 2 3 4
Выходные данные
0 1
Выбрано
:
|