Фирма Julick&Co ведет учет своих доходов и расходов. Но главный бухгалтер этой фирмы не любит математику, поэтому всякую сумму денег, которую фирма получает или отдает, он характеризует некоторым признаком. Например, сумму денег от 5 до 10 рублей он может охарактеризовать словом "МАЛО", а от 7 до 60 рублей словом "МНОГО". Время от времени он пересчитывает деньги и записывает признак суммы, которая имеется у фирмы. Недавно налоговая инспекция заинтересовалась доходами данной организации. Она хочет узнать, какая минимальная и максимальная сумма денег может быть сейчас у этой фирмы или выяснить, что имеется ошибка в ее записях. Известно, что по законам страны, где развиваются события, в любой момент времени организация должна обладать неотрицательной суммой денег.
Первая строка входного файла содержит \(K\) (\(1 \leq K \leq 100\)) – количество признаков, которые бухгалтер использует для описания различных сумм денег. На следующих \(K\) строках содержатся соответствующие признаки \(S_i\) и числа \(Min_i\) и \(Max_i\). \(S_i\) - слово, состоящие не более чем из \(20\) латинских букв, отделенное от последующих чисел одним пробелом, \(Min_i\) и \(Max_i\) - целые положительные числа (\(1 \leq Min_i \leq Max_i \leq 1000\)), разделенные одним пробелом. Следующая строка содержит количество денег, которое было у фирмы в начале ее деятельности – целое число . Затем следует число \(N\) – количество записей в бухгалтерской книге фирмы Julick&Co (\(1 \leq N \leq 100\)). Следующие N строк содержат записи в следующем формате: первый символ строки из множества {"+", "-", "!"} означает вид операции – доход, расход или подсчет денег соответственно. Непосредственно за этим символом (без пробелов) следует признак, характеризующий сумму денег, использованную в операции.
Если в учетных записях содержится ошибка, выведите в выходной файл число \(-1\), в противном случае выведите числа \(Min\) и \(Max\) - наименьшую и наибольшую сумму денег, которая может быть у фирмы Julick&Co.
3 LITTLE 1 5 MIDDLE 4 10 BIG 18 50 11 3 +MIDDLE !BIG -LITTLE
13 20
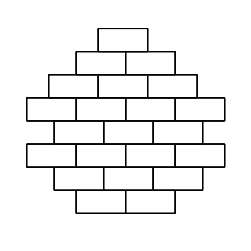
Воодушевленный легендой о Вавилонской Башне, Петя решил построить ее аналог у себя в комнате, для этого он взял \(N\) детских строительных кирпичиков, выбрал для себя размер основания \(D\) и высоту башни \(H\). Кроме того, он решил для себя, что размер каждого следующего уровня будет отличаться от предыдущего на один. Башня, показанная на рисунке, удовлетворяет Петиным запросам, имеет основание \(2\), высоту \(8\), и составлена из \(22\) кирпичиков.
Ваша задача состоит в том, чтобы написать программу, которая определяет, можно ли построить башню при выбранных Петей параметрах, и если да, то выдает сколько кирпичей должно быть на каждом уровне.
Во входном файле находятся числа \(N\), \(D\), и \(H\), разделенные пробелами (\(1 \leq N \leq 1000\), \(1 \leq D,H \leq 30\)).
Если башня, удовлетворяющая Петиным запросам существует, выведите в выходной файл \(N\) чисел – проект любой такой башни – количество кирпичиков на каждом уровне, начиная с самого нижнего. В противном случае выведите \(0\).
22 2 8
2 3 4 3 4 3 2 1
На сырном заводе во Флатландии живут мыши. Они очень любят сыр и часто уничтожают запасы сыра, приготовленные для отправки в магазин.
Всего на заводе живет \(m\) мышей. Для \(i\)-й мыши известна ее скорость поедания сыра \(s_i\), мышь может съесть \(s_i\) грамм сыра в час.
Недавно мышам стал известен план работы завода на ближайшее время. Планируется изготовить \(n\) головок сыра. Про каждую головку известны \(r_i\) к началу какого часа она будет изготовлена, \(d_i\) в начале какого часа она начнет портиться, и \(p_i\) вес головки сыра в граммах.
Мыши решили съесть весь сыр. В любой момент времени каждая мышь может есть некоторую головку сыра. Мыши существа брезгливые, и одну и ту же головку сыра не могут есть одновременно несколько мышей. При этом в любой момент времени мышь может решить прекратить есть головку сыра и приняться за другую, в том числе ту, которую ранее ела другая мышь.
Мыши не любят есть сыр после того как он начал портиться. Но оставлять сыр недоеденным мыши не могут. Они решили организовать поедание сыра таким образом, чтобы величина \(t\), такая что какую-либо головку все еще продолжают есть через \(t\) часов после того как она начала портиться, была минимальна. Помогите мышам выяснить, как это сделать.
Первая строка входного файла содержит два целых числа \(n\) и \(m\) (\(1 \le n \le 30\), \(1 \le m \le 30\)). Следующие \(n\) строк содержит по три целых числа: \(p_i\), \(r_i\) и \(d_i\) (\(1 \le p_i \le 10^5\), \(0 \le r_i \lt d_i \le 10^7\)). Далее следуют \(m\) строк, каждая из которых содержит по одному целому числу \(s_j\) (\(1 \le s_j \le 10^5\)).
Выведите одно вещественное число — искомое минимальное \(t\). Ваш ответ должен отличаться от правильного не больше чем на \(10^{-4}\).
Комментарий к примеру тестов
В первом примере мышам следует организовать поедание сыра следующим образом. Сначала первая мышь начинает есть первую головку сыра. Когда появляется вторая головка, она перестает есть первую и начинает есть вторую (в этот момент от первой осталось 9 граммов). Вторая мышь принимается есть первую головку сыра. Через 2.5 часа первая мышь доедает вторую головку сыра (на 0.5 часа позже чем она начала портиться) и снова начинает есть первую (вторая мышь за это время съела еще 5 граммов от первой головки и от нее осталось 4 грамма). Таким образом еще за час первая мышь доедает первую головку, также на 0.5 часа позже чем она начала портиться.
Во втором примере мышь успевает съесть сыр до того как он начинает портиться
2 2 13 0 4 10 1 3 4 2
0.5
1 1 1 0 1 1
0.0
Вова проводит соревнования и тренировки по программированию в своей школе. Для этого он скачал из Интернета много архивов разных соревнований и сборов по программированию. Он разархивировал все, что скачал, на жесткий диск своего компьютера, и теперь не может разобраться в получившемся наборе файлов. Вова хочет понять, сколько описаний соревнований по программированию он скачал.
Пара файлов называется тестом, если они находятся в одном каталоге и имеют полные имена вида «XY» и «XY.a», где «XY» — номер теста (дополненный ведущим нулем, если он меньше десяти). В первом из указанных файлов хранятся входные данные, а во втором — эталонный ответ.
Каталог называется каталогом с тестами, если в нем есть тесты со всеми номерами от \(1\) до \(N\), где \(1 \le N \le 99\), а других файлов нет (но могут быть подкаталоги).
Каталог называется задачей, если в нем есть файл с именем «check» и любым (возможно пустым) расширением и подкаталог «tests», который является каталогом с тестами. В каталоге-задаче помимо этого могут быть другие файлы и подкаталоги.
Каталог называется описанием соревнования, если в нем есть хотя бы один подкаталог, и все его подкаталоги являются задачами.
Задано описание всех файлов, хранящихся на жестком диске Вовиного компьютера. Необходимо найти, сколько описаний соревнований содержится на его жестком диске.
Первая строка входного файла содержит \(n\) — число файлов (\(1 \le n \le 1000\)). Каждая из последующих \(n\) строк содержит полный путь к файлу. Каждая из этих строк содержит от одного до 200 символов.
Элементы пути разделены символами «\». В начале элемента пути идет буква диска (от «A» до «Z»), затем следует двоеточие, затем «\». Имена каталогов в пути и имена файлов состоят из символов с кодами от 33 до 126, за исключением символа «\». Последний элемент пути является полным именем файла. Полное имя файла содержит не более одной точки, при этом до и после точки идет хотя бы один символ. Если имя файла содержит точку, то часть имени после точки называется расширением, а часть до точки — именем файла. Иначе считается, что файл имеет пустое расширение, а имя файла совпадает с его полным именем.
Строчные и заглавные буквы в путях не различаются. Ни в каком каталоге нет файла и подкаталога, имеющих одинаковые имена.
В выходной файл выведите количество описаний соревнований по программированию, которые содержатся в описанном наборе файлов.
22 C:\olymp\roi2005\aplusb\tests\01 C:\olymp\roi2005\aplusb\tests\01.a C:\olymp\roi2005\aplusb\tests\02 C:\olymp\roi2005\aplusb\tests\02.a C:\olymp\roi2005\aplusb\check.exe C:\olymp\roi2005\gcd\tests\01 C:\olymp\roi2005\gcd\tests\01.a C:\olymp\roi2005\gcd\tests\02 C:\olymp\roi2005\gcd\tests\02.a C:\olymp\roi2005\gcd\check.cpp C:\olymp\roi2005\gcd\solution.exe C:\olymp\roi2006\aplusb\tests\01 C:\olymp\roi2006\aplusb\tests\01.a C:\olymp\roi2006\aplusb\tests\03 C:\olymp\roi2006\aplusb\tests\03.a C:\olymp\roi2006\aplusb\check.exe C:\olymp\roi2006\gcd\tests\01 C:\olymp\roi2006\gcd\tests\01.a C:\olymp\roi2006\gcd\tests\03 C:\olymp\roi2006\gcd\tests\02.a C:\olymp\roi2006\gcd\check.cpp C:\olymp\roi2006\gcd\solution.exe
1
Две страны Байтландия и Флатландия решили объединить свои усилия в исследованиях в области физики высоких энергий и построили \(n\) адронных коллайдеров. Каждый коллайдер имеет форму кольца и находится под землей. При этом можно считать, что толщина каждого из коллайдеров пренебрежимо мала — их можно считать окружностями.
Как известно, адронные коллайдеры — устройства сложные и требующие постоянного внимания. Ни одна из стран не хочет брать на себя обслуживание всех коллайдеров, поэтому было решено поделить обслуживание коллайдеров между странами. Для того чтобы все было честно, было решено, что каждая из стран будет обслуживать ровно половину каждого из коллайдеров. Границу зон ответственности было решено провести в виде окружности. Таким образом, необходимо найти окружность, которая разбивает каждый из коллайдеров на две равные по длине части (то есть пересекает каждый из них в двух диаметрально противоположных точках).
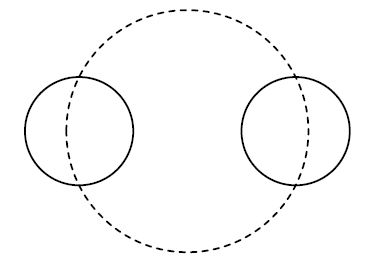
Требуется написать программу, которая по описанию построенных коллайдеров найдет окружность, удовлетворяющую указанным требованиям.
Первая строка входного файла содержит целое число \(n\) (\(1 \le n \le 3\)). Каждая из последующих \(n\) строк содержит описание одного из коллайдеров. Описание коллайдера состоит из трех целых чисел: \(x\), \(y\), \(r\) — координат центра коллайдера и его радиуса (\(|x|\), \(|y|\) \(\le 1000\), \(1\) \(\le r\) \(\le 1000\)). Коллайдеры не имеют общих точек, не лежат один внутри другого, а их центры (если \(n = 3\)) не находятся на одной прямой.
В первой строке выходного файла описание искомой границы: координаты центра окружности и радиус. Выводите как можно больше знаков после десятичной точки. При проверке правильности ответа, погрешности, не превышающие \(10^{-5}\), будут игнорироваться.
Координаты центра и радиус окружности не должны превосходить \(10^7\) по абсолютной величине. Гарантируется, что существует решение, удовлетворяющее указанному ограничению.
2 2 0 1 -2 0 1
0.0 0.0 2.23606797749979
3 0 10 1 0 0 2 10 10 3
5.4 4.85 7.52877812131557