Вася пишет новую версию своего офисного пакета "Closed Office". Недавно он начал работу над редактором "Dword", входящим в состав пакета.
Последняя проблема, с которой столкнулся Вася --- размещение рисунков в документе. Он никак не может добиться стабильного отображения рисунков в тех местах, в которые он их помещает. Окончательно отчаявшись написать соответствующий модуль самостоятельно, Вася решил обратиться за помощью к вам. Напишите программу, которая будет осуществлять размещение документа на странице.
Документ в формате редактора "Dword" представляет собой последовательность абзацев. Каждый абзац представляет собой последовательность элементов – слов и рисунков. Элементы одного абзаца разделены пробелами и/или переводом строки. Абзацы разделены пустой строкой. Строка, состоящая только из пробелов, считается пустой.
Слово --- это последовательность символов, состоящая из букв латинского алфавита, цифр, и знаков препинания: ".", ",", ":", ";", "!", "?", "-", "'".
Рисунок описывается следующим образом: "(image
| Параметр | Описание |
| width | Целое положительное число – ширина рисунка в пикселях |
| height | Целое положительное число – высота рисунка в пикселях |
| layout | Одно из следующих значений: embedded (в тексте), surrounded (обтекание текстом), floating (свободное) – описывает расположение рисунка относительно текста |
Документ размещается на бесконечной вверх и вниз странице шириной \(w\) пикселей (разбиение на конечные по высоте страницы планируется в следующей версии редактора). Одна из точек на левой границе страницы условно считается точкой с ординатой равной нулю. Ордината увеличивается вниз.
Размещение документа происходит следующим образом. Абзацы размещаются по очереди. Первый абзац размещается так, что его верхняя граница имеет ординату 0.
Абзац размещается следующим образом. Элементы располагаются по строкам. Каждая строка исходно имеет высоту \(h\) пикселей. В процессе размещения рисунков высота строк может увеличиваться, и строки могут разбиваться рисунками на фрагменты.
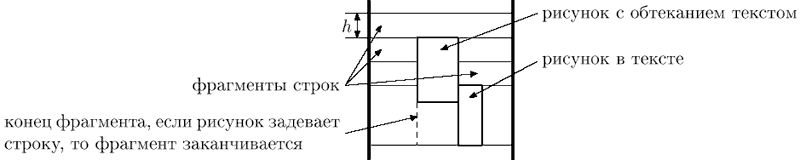
Слова размещаются следующим образом. Считается, что каждый символ имеет ширину \(c\) пикселей. Перед каждым словом, кроме первого во фрагменте, ставится пробел шириной также в \(c\) пикселей. Если слово помещается в текущем фрагменте, то оно размещается на нем. Если слово не помещается в текущем фрагменте, то оно размещается в первом фрагменте текущей строки, расположенном правее текущего, в котором оно помещается. Если такого фрагмента нет, то начинается новая строка, и поиск подходящего фрагмента продолжается в ней. Слово всегда "прижимается" к верхней границе строки.
Размещение рисунка зависит от его расположения относительно текста.
Если расположение рисунка относительно текста установлено в "\(embedded\)", то он располагается так же, как слово, за тем исключением, что его ширина равна ширине, указанной в параметрах рисунка. Кроме того, если высота рисунка больше текущей высоты строки, то она увеличивается до высоты рисунка (при этом верхняя граница строки не перемещается, а смещается вниз нижняя граница). Если рисунок типа "\(embedded\)" не первый элемент во фрагменте, то перед ним ставится пробел шириной \(c\) пикселей. Рисунки типа "\(embedded\)" также прижимаются к верхней границе строки.
Если расположение рисунка относительно текста установлено в "\(surrounded\)", то рисунок размещается следующим образом. Сначала аналогично находится первый фрагмент, в котором рисунок помещается по ширине. При этом перед рисунком этого типа не ставится пробел, даже если это не первый элемент во фрагменте.
После этого рисунок размещается следующим образом: верхний край рисунка совпадает с верхней границей строки, в которой находится найденный фрагмент, а сам рисунок продолжается вниз. При этом строки, через которые он проходит, разбиваются им на фрагменты.
Если расположение рисунка относительно текста установлено в "\(floating\)", то рисунок размещается поверх текста и других рисунков и никак с ними не взаимодействует. В этом случае у рисунка есть два дополнительных параметра: "\(dx\)" и "\(dy\)" --- целые числа, задающие смещение в пикселях верхнего левого угла рисунка вправо и вниз, соответственно, относительно позиции, где находится верхний правый угол предыдущего слова или рисунка (или самой левой верхней точки первой строки абзаца, если рисунок --- первый элемент абзаца).
Если при размещении рисунка таким образом он выходит за левую границу страницы, то он смещается вправо, так, чтобы его левый край совпадал с левой границей страницы. Аналогично, если рисунок выходит за правую границу страницы, то он смещается влево, чтобы его правый край совпадал с правой границей страницы.
Верхняя граница следующего абзаца совпадает с более низкой точкой из нижней границы последней строки и самой нижней границы рисунков типа "\(surrounded\)" предыдущего абзаца.
По заданным \(w\), \(h\), \(c\) и документу найдите координаты верхних левых углов всех рисунков в документе.
В первой строке вводятся три целых числа: \(w\), \(h\) и \(c\) (\(1 \le w \le 1000\), \(1 \le h \le 50\), \(1 \le c \le w\)).
Далее следует документ. Размер входных данных не превышает \(1000\) байт. Гарантируется, что ширина любого слова и любого рисунка не превышает \(w\). Высота всех рисунков не превышает 1000. Относительное смещение всех рисунков типа "\(floating\)" не превышает \(1000\) по абсолютной величине.
Выведите по два числа для каждого рисунка --- координаты его верхнего левого угла. Выводите координаты рисунков в том порядке, в котором они встречаются во входных данных.
Рисунок к примеру
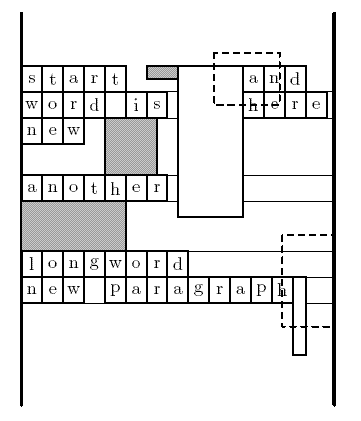
120 10 8 start (image layout=embedded width=12 height=5) (image layout=surrounded width=25 height=58) and word is (image layout=floating dx=18 dy=-15 width=25 height=20) here new (image layout=embedded width=20 height=22) another (image layout=embedded width=40 height=19) longword new paragraph (image layout=surrounded width=5 height=30) (image layout=floating width=20 height=35 dx=50 dy=-16)
48 0 60 0 74 -5 32 20 0 52 104 81 100 65
Сегодня на страницах газеты «Математический досуг» была опубликована необычная математическая головоломка. Одна из страниц газеты полностью занята прямоугольной таблицей, состоящей из m строк и n столбцов. В каждой ячейке таблицы записано некоторое целое число.
Для решения головоломки требуется найти такой невырожденный прямоугольник с вершинами в центрах ячеек таблицы, и сторонами, параллельными сторонам таблицы, чтобы сумма чисел, записанных в ячейках на границе получившегося прямоугольника, была максимальна.
Безуспешно потратив несколько часов на решение головоломки, Саша решил написать программу, которая сделала бы это за него. Но и тут его постигла неудача. Теперь ему ничего не остается, как обратиться за помощью к вам.
Напишите программу, которая по заданной таблице найдет искомый прямоугольник.
В первой строке вводятся два целых числа \(m\) и \(n\) (\(2 \le m, n \le 300\)). Далее следует описание таблицы – \(m\) строк, каждая из которых содержит по \(n\) целых чисел \(a_{i, j}\) (\(-10^4 \le a_{i,j} \le 10^4\)).
В первой строке выведите целое число \(s\) – максимальную сумму чисел на границе искомого прямоугольника. Во второй строке выведите четыре натуральных числа: \(x_1\), \(y_1\), \(x_2\), \(y_2\) – координаты левой верхней и правой нижней ячейки выбранного прямоугольника, соответственно (здесь \(x\) – номер строки, а \(y\) – номер столбца, строки нумеруются сверху вниз, начиная с единицы, столбцы нумеруются слева направо, начиная с единицы). Если оптимальных решений несколько, выведите любое.
2 3 1 1 1 1 1 1
6 1 1 2 3
5 4 9 -2 -1 3 -10 -5 1 -4 1 -1 2 -2 3 0 0 -1 2 2 -1 2
8 3 1 5 3
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более, чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
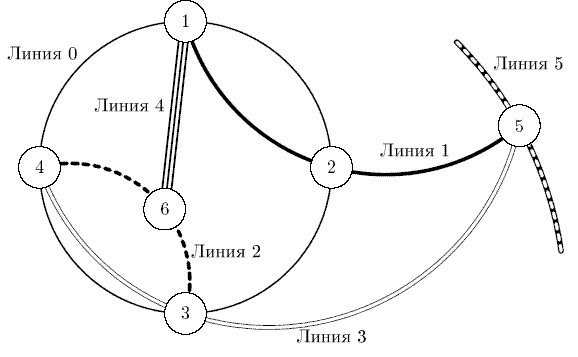
На рисунке приведена возможная схема метро, соответствующая второму примеру.
В первой строке вводится число k – количество линий метро в городе ( 1
k10). Все линии пронумерованы от 0 до k - 1, кольцевая линия имеет номер 0. Во второй строке записано число n – количество пересадочных станций. Каждая из следующих n строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
4 6 2 0 1 2 0 2 2 0 3 2 0 1 2 0 2 2 0 3
NO
6 6 3 0 1 4 2 0 1 3 0 2 3 3 0 2 3 3 1 3 5 2 2 4
YES
Вася написал на длинной полоске бумаги большое число и решил похвастаться своему старшему брату Пете этим достижением. Но только он вышел из комнаты, чтобы позвать брата, как его сестра Катя вбежала в комнату и разрезала полоску бумаги на несколько частей. В результате на каждой части оказалось одна или несколько идущих подряд цифр.
Теперь Вася не может вспомнить, какое именно число он написал. Только помнит, что оно было очень большое. Чтобы утешить младшего брата, Петя решил выяснить, какое максимальное число могло быть написано на полоске бумаги перед разрезанием. Помогите ему!
Входные данные состоят из одной или более строк, каждая из которых содержит последовательность цифр. Количество строк не превышает 100, каждая строка содержит от 1 до 100 цифр. Гарантируется, что хотя бы в одной строке первая цифра отлична от нуля.
Выведите одну строку – максимальное число, которое могло быть написано на полоске перед разрезанием.
2 20 004 66
66220004
3
3
Когда пользователь работает в операционной системе Windows, у него часто запущено несколько приложений. Каждое из приложений работает в отдельном окне. Для переключения между окнами используется комбинация клавиш «Alt+Tab». Эта комбинация делает активным окно, в котором пользователь работал перед тем, как перейти в текущее активное окно.
Чтобы переключиться в другое окно, можно нажать клавишу «Alt» и затем, не отпуская ее, несколько раз нажать клавишу «Tab». Чтобы понять, какое окно станет активным после этого, воспользуемся следующей моделью. Пусть запущено n приложений. Приложения в операционной системе организованы в виде списка и упорядочены по убыванию времени последней активности. То есть приложение, окно которого является активным в настоящий момент – первое в списке, приложение, окно которого было активно перед этим – второе, и т. д.
Если нажать клавишу «Alt» и затем, не отпуская ее, нажать клавишу «Tab» k раз, то активным станет окно приложения, которое находится на (k mod n) + 1-м месте в списке. Здесь a mod b означает остаток от деления a на b. Иными словами, операционная система рассматривает список как циклический, переходя после последнего элемента списка к первому.
При запуске нового приложения оно добавляется в начало списка.
Задана последовательность действий пользователя, где каждое действие – либо запуск приложения, либо переключение между окнами. Выведите список имен приложений в том порядке, в котором с ними работал пользователь.
В первой строке вводится целое число n – количество действий пользователя ( 1n1000). Следующие n строк содержат описание действий пользователя.
Запуск приложения описывается строкой «Run <имя приложения»>. Здесь «<имя приложения»> – строка из не более чем 100 латинских букв, цифр и пробелов. Она отделена от слова «Run» ровно одним пробелом. Все имена приложений различны. Большие и маленькие буквы считаются различными.
Переключение между приложениями описывается строкой «Alt+Tab+...+Tab», здесь подстрока «+Tab» повторена в точности столько раз, сколько раз пользователь нажал клавишу «Tab», не отпуская клавишу «Alt». Это количество не превышает 100.
Первая команда во входных данных – всегда команда «Run».
Выведите n строк – последовательность имен приложений, с которыми работал пользователь в порядке, в котором их окна становились активными.
6 Run Mozilla Firefox Run Free Pascal Alt+Tab Run Miranda IM Alt+Tab+Tab Alt+Tab+Tab+Tab
Mozilla Firefox Free Pascal Mozilla Firefox Miranda IM Free Pascal Free Pascal