Год назад Флатландию потряс серьезный экономический кризис, после которого, с целью снижения издержек, фермер Джон и фермер Билл решили объединить свои фермы. За год совместной продуктивной работы на объединенной территории было построено четыре сарая.
Однако последствия кризиса в последнее время ощущаются все меньше, да и совместное ведение хозяйства – дело непростое. Поэтому фермеры решили снова разделить свои фермы.
Для раздела ферм решено было построить забор. Разумеется, прежде чем приступить к строительству, фермеры взяли карту совместного хозяйства и стали обсуждать возможное положение забора. Забор должен представлять собой прямую линию. Поскольку по закону границы участков должны быть направлены либо с севера на юг, либо с запада на восток, забор на карте должен представлять собой прямую, параллельную краю карты – вертикальную либо горизонтальную.
Единственная проблема – четыре построенных за год совместной работы сарая. Разумеется, каждому фермеру в результате раздела должно достаться по два сарая. Поэтому после постройки забора два сарая должны оказаться с одной стороны от него, а два других – с другой.
Помогите фермерам найти такое положение для забора. Забор может проходить непосредственно вдоль стены сарая.
На вход программы поступают четыре четверки целых чисел. Каждая четверка описывает один сарай. Первые два числа в описании сарая – это координаты на карте его левого нижнего угла, следующие два числа – координаты правого верхнего угла.
Система координат размещена таким образом, что ось OX направлена слева направо, а ось OY – снизу вверх. Оси координат параллельны краям карты. Стороны сараев также параллельны краям карты. Сараи не имеют общих точек. Каждый сарай имеет ненулевую площадь. Все координаты неотрицательны и не превышают 109.
Если построить забор, удовлетворяющий всем условиям, невозможно, выведите слово «Impossible».
В противном случае в первой строке выведите слово «Vertical», если забор следует построить параллельно вертикальному краю карты, или слово «Horizontal», если забор следует построить параллельно горизонтальному краю карты.
В следующей строке выведите координату x всех точек забора, если он должен быть вертикальным, либо координату y всех точек забора, если он должен быть горизонтальным. Выведенная координата должна быть целым числом (несложно показать, что если забор можно построить, то его можно построить так, чтобы искомая координата была целой).
Приведенные ниже рисунки соответствуют примерам входных данных.
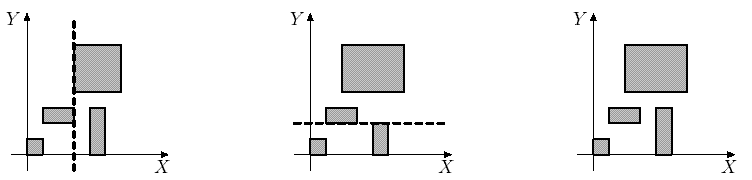
0 0 1 1 1 2 3 3 4 0 5 3 3 4 6 7
Vertical 3
0 0 1 1 1 2 3 3 4 0 5 2 2 4 6 7
Horizontal 2
0 0 1 1 1 2 3 3 4 0 5 3 2 4 6 7
Impossible
Сережа очень любит старые игры. Недавно он нашел у себя на компьютере одну старую приключенческую игру. Управляя героем, надо перемещаться по карте и собирать различные предметы.
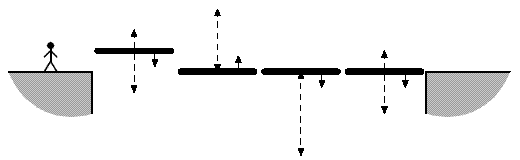
На определенном этапе игры Сережа столкнулся с неожиданной проблемой. Для продолжения приключений герою надо перебраться через пропасть. Для этого можно использовать последовательно расположенные лифты, которые имеют вид горизонтальных платформ. Каждый лифт вертикально перемещается туда-сюда между некоторыми уровнями. Герой может переходить между соседними платформами, однако это можно сделать только в тот момент, когда они находятся на одном уровне. Аналогично, с края пропасти на лифт и обратно можно перейти лишь в тот момент, когда лифт окажется на уровне края.
Каждый лифт имеет ширину, равную четырем метрам. В начале герой находится на расстоянии два метра от края пропасти. Он должен закончить свое путешествие в двух метрах от противоположного края пропасти. Герой перемещается со скоростью два метра в секунду. Таким образом, если герой находится в начальном положении или в центре лифта и хочет перейти на соседний лифт (или сойти с последнего лифта на противоположный край пропасти), он должен начать движение ровно за одну секунду до того момента, когда они окажутся на одном уровне. Через две секунды герой оказывается в центре соседнего лифта (или в конечном положении).
Края пропасти находятся на одном уровне. Для каждого лифта задан диапазон высот, между которыми он перемещается, начальное положение и направление движения в начальный момент. Все лифты перемещаются со скоростью один метр в секундy. Выясните, сможет ли герой перебраться на противоположный край пропасти, и если да, то какое минимальное время ему для этого понадобится.
В первой строке вводится целое число n – количество лифтов ( 1
n100). Следующие n строк содержат описания лифтов.
Каждое описание состоит из четырех целых чисел: l, u, s – самое нижнее, самое верхнее и начальное положение лифта относительно края пропасти в метрах ( -100lsu100, l < u), и d – направление движения лифта в начальный момент (d = 1 означает, что лифт двигается вверх, d = - 1 – вниз).
Выведите минимальное время в секундах, необходимое для того, чтобы перебраться на противоположный край пропасти. Если перебраться на противоположный край пропасти невозможно, выведите число -1.
4 -1 2 1 -1 0 3 0 1 -4 0 0 -1 -2 1 0 -1
29
Сверхсекретный завод, расположенный высоко в горах, занимается изготовлением новейших систем контроля торсионных полей – нанокристаллов. Нанокристалл состоит из нескольких атомов, некоторые из которых попарно связаны сверхпрочными торсионными связями.
Нанокристалл стабилен, если между любыми двумя его атомами можно построить соединяющую их цепочку связей, возможно с использованием других атомов. Например, нанокристалл 
из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.
Для любой пары атомов стабильного нанокристалла определена их взаимная удаленность – минимальная длина цепочки из связей, которая их соединяет. Например, рассмотрим описанный выше нанокристалл . Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).
Важнейшей характерикой стабильного нанокристалла является его емкость. Емкость нанокристалла равна сумме взаимных удаленностей всех пар его атомов. Например, емкость нанокристалла равна 8.
Недавно на завод поступил заказ – разработать стабильный нанокристалл заданной емкости c. При этом как число атомов в нанокристалле, так и число связей может быть произвольным. Помогите ученым разработать такой кристалл!
На вход программы поступает число c ( 1c10 000).
В первой строке выведите два целых числа n и m – количество атомов и связей в разработанном нанокристалле, соответственно. Будем считать, что атомы нанокристалла пронумерованы от 1 до n. Следующие m строк должны содержать по два целых числа – пары атомов, которые следует соединить торсионными связями. Если решений несколько, выведите любое.
Если искомого нанокристалла не существует, выведите в первой и единственной строке выходных данных два нуля.
2
0 0
8
4 4 1 2 1 3 1 4 3 4
Выполняя очередное задание Министерства образования и сельского хозяйства, программисты Флатландского государственного университета информационных технологий, удобрений и ядохимикатов создали специального робота по прокладке оросительных каналов.
Программа для робота представляет собой последовательность команд. Команды робота приведены в следующей таблице:
| Команда | Обозначение | Действия робота |
| Перемещение | (X) | Переместиться вперед на X километров, прокладывая за собой оросительный канал |
| Поворот налево | L | Повернуть налево на 90o |
| Поворот направо | R | Повернуть направо на 90o |
Любая программа начинается и заканчивается командами перемещения и не содержит двух команд перемещения или двух команд поворота подряд.
Исходно робот размещается в некоторой точке поля, на котором требуется создать оросительную систему. После запуска робот последовательно выполняет команды своей программы. Программа считается корректной, если полученный в результате ее выполнения канал не имеет самопересечений или самокасаний.
Программисты университета написали программу и собрались отправить ее по электронной почте в министерство. Однако, в результате поражения сети университета вирусом программа оказалась испорчена. А именно, из нее исчезли все команды перемещения. Теперь программистам требуется восстановить программу. Поскольку времени очень мало, решено было оставить сохранившиеся команды поворота, вставив между ними команды перемещения так, чтобы получившаяся программа была корректной.
Входные данные содержат команды поворота исходной программы в том порядке, в котором они в ней следовали. Каждая команда представляет собой символ «L» либо «R», команды друг от друга не отделяются. Количество команд не превышает 30 000.
Выведите любую корректную программу, последовательность команд поворота в которой совпадает с последовательностью, заданной во входных данных. Параметр X каждой команды перемещения должен быть положительным целым числом и не должен превышать 109. Все команды выведите в одной строке и друг от друга не отделяйте.
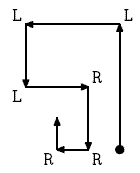
LLLRRR
(4)L(3)L(1)L(2)R(2)R(1)R(1)
Недавно на лесопилку, где работает Вася, поступил новый заказ. Для постройки нового дома мэру соседнего города требуется a досок длины x футов и b досок длины y футов.
Поскольку на лесопилке имеется только неограниченный запас досок длины z футов, Васе поручили исполнить заказ клиента, распилив имеющиеся доски на меньшие. Вася хочет закончить работу как можно быстрее, поэтому он хочет выполнить заказ, сделав как можно меньше распилов. При этом количество использованных досок длины z роли не играет, кроме того, часть досок, образовавшихся в результате распила, может не требоваться для заказа и остаться на лесопилке.
Например, если на лесопилке имеются доски длины 80, а клиенту требуется две доски длины 30 и семь досок длины 20, то достаточно сделать семь распилов: одну доску распилить двумя распилами на доски длины 20, 30 и 30, одну тремя распилами на четыре доски длины 20 и одну двумя распилами на доски длины 20, 20 и 40. Доска длины 40 клиенту не нужна, она останется на лесопилке, остальные доски будут отправлены клиенту.
На вход программы поступают числа \(a, x, b, y \) и \( z \). Все числа положительны и не превышают 300, \( x \le z, y \le z, x \neq y \).
Выведите минимальное количество распилов, которые требуется сделать для того, чтобы выполнить заказ.
2 30 7 20 80
7