Сортировка записей(9 задач)
Использование сортировки(13 задач)
Быстрая сортировка(55 задач)
Сортировка слиянием(9 задач)
Сортировка подсчетом(27 задач)
Сканирующая прямая(39 задач)
Сортировка событий(4 задач)
Задана информация об N партиях - количестве голосующих за них и размер взятки, который необходимо дать партии, чтобы она делала что нужно, если победит. Изменение результата голосования одного человека стоит 1 уе. Требуется за наименьшее количество денег подкупить партию и людей так, чтобы она победила.
В одной демократической стране приближаются парламентские выборы. Выборы проходят по следующей схеме: каждый житель страны, достигший восемнадцатилетнего возраста, отдает свой голос за одну из политических партий. После этого партия, которая набрала максимальное количество голосов, считается победившей на выборах и формирует правительство. Если несколько партий набрали одинаковое максимальное количество голосов, то они должны сформировать коалиционное правительство, что обычно приводит к длительным переговорам.
Один бизнесмен решил выгодно вложить свои средства и собрался поддержать на выборах некоторые партии. В результате поддержки он планирует добиться победы одной из этих партий, которая затем сформирует правительство, которое будет действовать в его интересах. При этом возможность формирования коалиционного правительства его не устраивает, поэтому он планирует добиться строгой победы одной из партий.
Чтобы повлиять на исход выборов, бизнесмен собирается выделить деньги на агитационную работу среди жителей страны. Исследование рынка показало, что для того, чтобы один житель сменил свои политические воззрения, требуется потратить одну условную единицу. Кроме того, чтобы i-я партия в случае победы сформировала правительство, которое будет действовать в интересах бизнесмена, необходимо дать лидеру этой партии взятку в размере pi условных единиц. При этом некоторые партии оказались идеологически устойчивыми и не согласны на сотрудничество с бизнесменом ни за какие деньги.
По результатам последних опросов известно, сколько граждан планируют проголосовать за каждую партию перед началом агитационной компании. Помогите бизнесмену выбрать, какую партию следует подкупить, и какое количество граждан придется убедить сменить свои политические воззрения, чтобы выбранная партия победила, учитывая, что бизнесмен хочет потратить на всю операцию минимальное количество денег.
В первой строке вводится целое число n – количество партий ( 1<= n <=105). Следующие n строк описывают партии. Каждая из этих строк содержит по два целых числа: vi – количество жителей, которые собираются проголосовать за эту партию перед началом агитационной компании, и pi – взятка, которую необходимо дать лидеру партии для того, чтобы сформированное ей в случае победы правительство действовало в интересах бизнесмена ( 1<=vi<=106, 1<=pi<=106 или pi = - 1). Если партия является идеологически устойчивой, то pi равно -1. Гарантируется, что хотя бы одно pi не равно -1.
В первой строке выведите минимальную сумму, которую придется потратить бизнесмену. Во второй строке выведите номер партии, лидеру которой следует дать взятку. В третьей строке выведите n целых чисел – количество голосов, которые будут отданы за каждую из партий после осуществления операции. Если оптимальных решений несколько, выведите любое.
3 7 -1 2 8 1 2
6 3 3 2 5
Вася написал на длинной полоске бумаги большое число и решил похвастаться своему старшему брату Пете этим достижением. Но только он вышел из комнаты, чтобы позвать брата, как его сестра Катя вбежала в комнату и разрезала полоску бумаги на несколько частей. В результате на каждой части оказалось одна или несколько идущих подряд цифр.
Теперь Вася не может вспомнить, какое именно число он написал. Только помнит, что оно было очень большое. Чтобы утешить младшего брата, Петя решил выяснить, какое максимальное число могло быть написано на полоске бумаги перед разрезанием. Помогите ему!
Входные данные состоят из одной или более строк, каждая из которых содержит последовательность цифр. Количество строк не превышает 100, каждая строка содержит от 1 до 100 цифр. Гарантируется, что хотя бы в одной строке первая цифра отлична от нуля.
Выведите одну строку – максимальное число, которое могло быть написано на полоске перед разрезанием.
2 20 004 66
66220004
3
3
Скоро новый год и Санта-Клаус уже начал готовить свою волшебную оленью упряжку, на которой он развозит подарки детям. Известно, что упряжку везут несколько волшебных оленей, на каждом из которых едут два эльфа.
Но волшебные олени – строптивые животные, поэтому не любые два эльфа могут ехать на любом олене. А именно, каждый олень характеризуется некоторой строптивостью ai, а каждый эльф – темпераментом bi. Два эльфа j и k могут ехать на i-м олене в том и только в том случае, если либо \( b_j \lt a_i \lt b_k \), либо \( b_k \lt a_i \lt b_j\).
Чтобы его появление было максимально зрелищным, Санта-Клаус хочет, чтобы в его упряжке было как можно больше оленей. Про каждого оленя Санта знает его строптивость, а про каждого эльфа – его темперамент.
Помогите Санте выяснить, какое максимальное количество оленей он сможет включить в упряжку, каких оленей ему следует выбрать, и какие эльфы должны на них ехать.
В первой строке вводятся два целых числа m и n – количество оленей и эльфов, соответственно \( (1 \le m, n \le 100 000) \).
Вторая строка содержит m целых чисел ai – строптивость оленей \( (0 \le a_i \le 10^9) \). В третьей строке записаны \(n\) целых чисел \(b_i\) – темперамент эльфов \( (0 \le b_i \le 10^9) \).
В первой строке выведите одно число k – максимальное количество оленей, которое Санта-Клаус может включить в свою упряжку. В следующих k строках выведите по три целых числа: di, ei, 1, ei, 2 – для каждого оленя в упряжке выведите его номер и номера эльфов, которые на нем поедут. Если решений несколько, выведите любое.
И эльфы, и олени пронумерованы, начиная с единицы, в том порядке, в котором они заданы во входных данных.
4 6 2 3 4 5 1 3 2 2 5 2
2 1 1 2 2 4 5
Во Флатландии n городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание n - 1 шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды – числа от 1 до n.
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача – таким образом сопоставить числам от 1 до n города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
В первой строке вводится целое число n – количество городов во Флатландии ( 2![]() n
n![]() 1500).
1500).
Далее следует n описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города – строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа x и y – координаты города. Координаты не превышают 104 по абсолютной величине.
Далее следуют n - 1 строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа – номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более, чем одним шоссе.
Выведите n строк, i-я из этих строк должна содержать название города, который следует сопоставить числу i в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите строку «No solution».
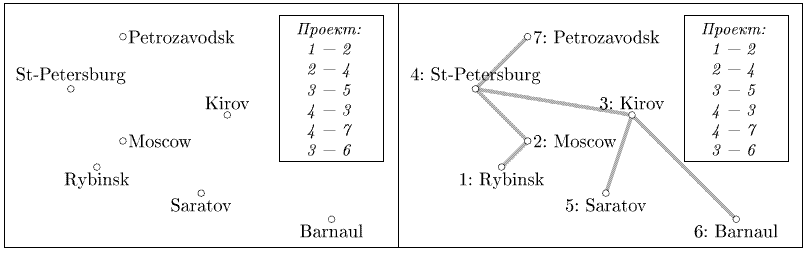
7 Moscow 2 2 St-Petersburg 0 4 Kirov 6 3 Saratov 5 0 Rybinsk 1 1 Petrozavodsk 2 6 Barnaul 10 -1 1 2 2 4 3 5 4 3 4 7 3 6
St-Petersburg Rybinsk Kirov Saratov Moscow Petrozavodsk Barnaul
Ваня очень любит шахматы. Причем он не только любит просто играть в шахматы, но часто придумывает разные головоломки и просто забавные задачки с использованием шахматных фигур. Также вместо стандартной шахматной доски 8×8 Ваня часто использует в своих задачах доски другого размера.
Недавно он придумал новую головоломку и рассказал ее своим друзьям. Суть головоломки заключается в следующем. На одно из полей доски размером m×n записывается некоторое положительное целое число и затем на него ставится ферзь.
После этого Ваня делает k ходов ферзем, каждый раз перемещая его по шахматным правилам на одно из полей, на котором он еще не был. При этом каждый раз, перед тем как поставить ферзя на некоторое поле, он записывает на это поле целое число, причем это число всегда больше всех чисел, уже записанных на доске.
Задача друзей Вани – по числам, записанным на доске, восстановить маршрут ферзя или выяснить, что Ваня где-то ошибся. Поскольку Ваня часто выбирает достаточно большие m, n и k, друзья устали решать эту головоломку вручную и решили написать для ее решения программу. Помогите им
Напомним, что по шахматным правилам ферзь может пойти на любое поле доски, находящееся на одной вертикали, горизонтали или диагонали с тем полем, на котором он находится.
В первой строке вводятся числа m, n и k ( 1![]() m, n
m, n![]() 300, 0
300, 0![]() k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
Если Ваня ошибся при построении головоломки, выведите сообщение «Wrong Board».
В противном случае выведите m строк по n чисел – для каждого поля выведите номер хода, перед которым ферзь побывал на этом поле, а для последнего поля, на котором он оказался – число k + 1. Для полей, на которые ферзь не попадал, выведите число 0.
4 4 7 10 20 0 100 30 0 0 40 0 0 0 0 45 42 0 70
1 2 0 8 3 0 0 4 0 0 0 0 6 5 0 7
2 4 4 10 20 30 40 0 50 0 0
Wrong Board
2 2 2 1 2 4 3
Wrong Board