Скоро новый год и Санта-Клаус уже начал готовить свою волшебную оленью упряжку, на которой он развозит подарки детям. Известно, что упряжку везут несколько волшебных оленей, на каждом из которых едут два эльфа.
Но волшебные олени – строптивые животные, поэтому не любые два эльфа могут ехать на любом олене. А именно, каждый олень характеризуется некоторой строптивостью ai, а каждый эльф – темпераментом bi. Два эльфа j и k могут ехать на i-м олене в том и только в том случае, если либо \( b_j \lt a_i \lt b_k \), либо \( b_k \lt a_i \lt b_j\).
Чтобы его появление было максимально зрелищным, Санта-Клаус хочет, чтобы в его упряжке было как можно больше оленей. Про каждого оленя Санта знает его строптивость, а про каждого эльфа – его темперамент.
Помогите Санте выяснить, какое максимальное количество оленей он сможет включить в упряжку, каких оленей ему следует выбрать, и какие эльфы должны на них ехать.
В первой строке вводятся два целых числа m и n – количество оленей и эльфов, соответственно \( (1 \le m, n \le 100 000) \).
Вторая строка содержит m целых чисел ai – строптивость оленей \( (0 \le a_i \le 10^9) \). В третьей строке записаны \(n\) целых чисел \(b_i\) – темперамент эльфов \( (0 \le b_i \le 10^9) \).
В первой строке выведите одно число k – максимальное количество оленей, которое Санта-Клаус может включить в свою упряжку. В следующих k строках выведите по три целых числа: di, ei, 1, ei, 2 – для каждого оленя в упряжке выведите его номер и номера эльфов, которые на нем поедут. Если решений несколько, выведите любое.
И эльфы, и олени пронумерованы, начиная с единицы, в том порядке, в котором они заданы во входных данных.
4 6 2 3 4 5 1 3 2 2 5 2
2 1 1 2 2 4 5
На планете Плюк, поверхность которой мы будем считать абсолютно плоской, был разработан новый принцип перемещения единственного имеющегося там транспортного средства – пепелаца. А именно, на расстоянии одного километра друг от друга в точках (0, 0) и (1, 0) были построены две станции управления пепелацами A и B. С помощью них можно мгновенно переместить любой пепелац, повернув его на 90 градусов по или против часовой стрелки относительно точки A или B. Расстояние от пепелаца до соответствующей станции при этом не меняется. Следующее перемещение можно делать как относительно той же станции, так и относительно другой.
Например, если повернуть пепелац, находящийся в точке (3, 1) на 90 градусов против часовой стрелки относительно станции A, то он переместится в точку (- 1, 3), если его затем повернуть на 90 градусов по часовой стрелке относительно станции B, то он переместится в точку (4, 2), если затем повернуть его вокруг станции B по часовой стрелке еще раз, он переместиться в точку (3, - 3).
Один житель планеты недавно решил отправиться на своем пепелаце в гости к другу. Житель проживает около точки с координатами (x1, y1), а его друг – около точки с координатами (x2, y2). Помогите жителю с помощью станций управления пепелацем оказаться как можно ближе к месту, где проживает его друг, чтобы потом меньше было идти по пустыне.
Поскольку перемещения мгновенные и абсолютно бесплатные, то минимизировать количество перемещений не надо.
На вход программы поступают четыре целых числа – x1, y1, x2 и y2, они не превышают 104 по абсолютной величине.
Выведите последовательность перемещений с использованием станций управления, которая перемещает пепелац из точки (x1, y1) как можно ближе к точке (x2, y2).
Поворот по часовой стрелке относительно станции A обозначается как «+A», поворот против часовой стрелки относительно станции A обозначается как «-A», соответствующие повороты относительно станции B обозначаются как «+B» и «-B». Выводите по одному перемещению на строке.
Выведенная последовательность не обязана быть минимальной по количеству перемещений, но должна содержать не более 106 действий.
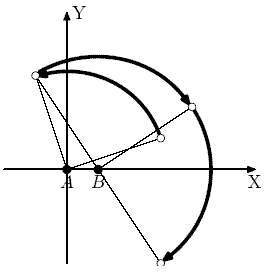
3 1 3 -3
+A -B -B +A +A -B -B +A
0 0 3 0
-A +B +A -B
Сверхсекретный завод, расположенный высоко в горах, занимается изготовлением новейших систем контроля торсионных полей – нанокристаллов. Нанокристалл состоит из нескольких атомов, некоторые из которых попарно связаны сверхпрочными торсионными связями.
Нанокристалл стабилен, если между любыми двумя его атомами можно построить соединяющую их цепочку связей, возможно с использованием других атомов. Например, нанокристалл ![]() из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.
из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.
Для любой пары атомов стабильного нанокристалла определена их взаимная удаленность – минимальная длина цепочки из связей, которая их соединяет. Например, рассмотрим описанный выше нанокристалл ![]() . Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).
. Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).
Важнейшей характерикой стабильного нанокристалла является его емкость. Емкость нанокристалла равна сумме взаимных удаленностей всех пар его атомов. Например, емкость нанокристалла ![]() равна 8.
равна 8.
Недавно на завод поступил заказ – разработать стабильный нанокристалл заданной емкости c. При этом как число атомов в нанокристалле, так и число связей может быть произвольным. Помогите ученым разработать такой кристалл!
На вход программы поступает число c ( 1![]() c
c![]() 10 000).
10 000).
В первой строке выведите два целых числа n и m – количество атомов и связей в разработанном нанокристалле, соответственно. Будем считать, что атомы нанокристалла пронумерованы от 1 до n. Следующие m строк должны содержать по два целых числа – пары атомов, которые следует соединить торсионными связями. Если решений несколько, выведите любое.
Если искомого нанокристалла не существует, выведите в первой и единственной строке выходных данных два нуля.
2
0 0
8
4 4 1 2 1 3 1 4 3 4
Выполняя очередное задание Министерства образования и сельского хозяйства, программисты Флатландского государственного университета информационных технологий, удобрений и ядохимикатов создали специального робота по прокладке оросительных каналов.
Программа для робота представляет собой последовательность команд. Команды робота приведены в следующей таблице:
| Команда | Обозначение | Действия робота |
| Перемещение | (X) | Переместиться вперед на X километров, прокладывая за собой оросительный канал |
| Поворот налево | L | Повернуть налево на 90o |
| Поворот направо | R | Повернуть направо на 90o |
Любая программа начинается и заканчивается командами перемещения и не содержит двух команд перемещения или двух команд поворота подряд.
Исходно робот размещается в некоторой точке поля, на котором требуется создать оросительную систему. После запуска робот последовательно выполняет команды своей программы. Программа считается корректной, если полученный в результате ее выполнения канал не имеет самопересечений или самокасаний.
Программисты университета написали программу и собрались отправить ее по электронной почте в министерство. Однако, в результате поражения сети университета вирусом программа оказалась испорчена. А именно, из нее исчезли все команды перемещения. Теперь программистам требуется восстановить программу. Поскольку времени очень мало, решено было оставить сохранившиеся команды поворота, вставив между ними команды перемещения так, чтобы получившаяся программа была корректной.
Входные данные содержат команды поворота исходной программы в том порядке, в котором они в ней следовали. Каждая команда представляет собой символ «L» либо «R», команды друг от друга не отделяются. Количество команд не превышает 30 000.
Выведите любую корректную программу, последовательность команд поворота в которой совпадает с последовательностью, заданной во входных данных. Параметр X каждой команды перемещения должен быть положительным целым числом и не должен превышать 109. Все команды выведите в одной строке и друг от друга не отделяйте.
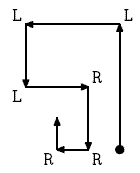
LLLRRR
(4)L(3)L(1)L(2)R(2)R(1)R(1)
На днях Алиса делала уборку в своей комнате и нашла дневник, который вела в начальной школе. Там она с удивлением обнаружила запись о том насколько ее поразило то, что \(2 + 2 = 2 \cdot 2\). Невероятно, умножение и сложение дают один и тот же результат!
Эта запись натолкнула Алису на следующую задачу: пусть целые заданы числа \(a\) и \(b\). Сколько различных значений в наборе чисел
| \(a + b\), | \(\;a - b\), | \(\;a \cdot b\), | \(\;a / b\), | \(\;a^b\), |
| \(b + a\), | \(\;b - a\), | \(\;b \cdot a\), | \(\;b / a\), | \(\;b^a\). |
Деление происходит без округления, результат деления может не быть целым числом. Если какое-либо выражение из этого набора некорректно, то Алиса его не рассматривает. Некорректными считаются деление на ноль и возведение нуля в неположительную степень.
Первая строка входного файла содержит целые числа \(a\) и \(b\), разделенные пробелом (\(|a|, |b| \le 10^9\)).
Выведите в выходной файл количество различных чисел в приведенном наборе.