Сегодня на уроке математики шестиклассник Петя изучил понятие наибольшего общего делителя. Петя тут же решил применить полученные знания на практике.
Петя выписал на листке бумаги \(n\) чисел \(a_1, \ldots, a_n\) --- номера домов, в которых живут его друзья. Теперь он хочет выбрать такое подмножество этих чисел, чтобы их наибольший общий делитель был равен его любимому числу \(d\).
Помогите Пете выбрать из выписанных чисел искомое подмножество.
Первая строка входного файла содержит два целых числа \(n\) и \(d\) (\(1 \le n \le 1000\), \(1 \le d \le 10^9\)). Вторая строка содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)).
Если существует искомое подмножество, выведите на первой строке выходного файла число \(k\) --- количество чисел в нем. На второй строке выведите числа, входящие в это подмножество.
Если решения не существует, выведите на первой строке выходного файла число \(-1\).
Если возможных ответов несколько, выведите любой из них.
4 3 6 8 12 9
2 6 9
3 3 2 4 8
-1
Фридрих III --- мэр обыкновенного средневекового города. Недавно на этот город стали совершать набеги кочевники. Город окружен надежной крепостной стеной, поэтому коренные жители города надежно защищены. К сожалению, бесчинство кочевников привело к наплыву беженцев, которые стали селиться у крепостной стены за пределами города. Именно они больше всего страдают от набегов. Фридрих считает, что защита беженцев входит в его обязанности, но в данный момент у города нет ресурсов на строительство дополнительной стены.
Оборона города на высоте, поэтому кочевники не рискуют приближаться вплотную к городу. Мэр заметил, что за пределами города существуют точки, которые не видны кочевникам до тех пор, пока те остаются достаточно далеко.
Более формально, представим крепостную стену как многоугольник \(P\). Назовем точку \(X\) защищенной многоугольником \(P\), если любой луч, проведенный из \(X\), пересекается с \(P\). Например, любая точка внутри \(P\) является защищенной. Множество всех защищенных точек также образует многоугольник. Назовем его \(Q\).


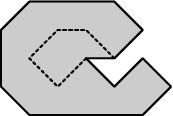
Мэр решил распространить среди беженцев карту защищенных точек, как мест, рекомендуемых для поселения. Требуется помочь ему составить эту карту.
Задан многоугольник \(P\), требуется найти многоугольник \(Q\), состоящий из точек, защищенных многоугольником \(P\).
Первая строка входного файла содержит целое число \(n\) --- число вершин многоугольника \(P\), соответствующего крепостной стене (\(3 \le n \le 100\)). Следующие \(n\) строк содержат по два целых числа \(x_i\) и \(y_i\), разделенных пробелом --- координаты \(i\)-й вершины многоугольника в порядке обхода по часовой стрелке (\(|x_i|, |y_i| \le 10\,000\)).
Выведите множество защищенных точек --- многоугольник \(Q\).
Сначала выведите число \(m\) --- число вершин многоугольника \(Q\). Следующие \(m\) строк должны содержать по два вещественных числа \(x_i\) и \(y_i\), разделенных пробелом --- координаты \(i\)-й вершины многоугольника в порядке обхода по часовой стрелке. Никакие три последовательные вершины не должны лежать на одной прямой.
Вещественные числа выводите с точностью не менее шести знаков после запятой.
3 0 0 0 1 1 0
3 0 0 0 1 1 0
16 0 1 0 3 1 4 4 4 5 3 4 2 3 3 2 3 1 2 2 1 3 2 4 1 5 2 6 1 5 0 1 0
12 0 1 0 3 1 4 4 4 5 3 4 2 3 2 4 1 5 2 6 1 5 0 1 0
Недавно Васе продиктовали номер телефона. Он записал его, разделив числа дефисами, но потом начал сомневаться, не ошибся ли он в записи номера. Ведь бывают различные телефонные номера, которые произносятся одинаково. Например, все четыре номера «3000-100-1», «3000-101», «3100-1», «3101» читаются как «три тысячи сто один». Теперь он хочет выяснить, какие номера произносятся также, как и записанный им номер.
Вася считает, что при произношении телефонного номера не употребляются числа, состоящие более чем из девяти цифр. Напомним, как произносятся числа от \(1\) до \(999\,999\,999\).
Если число больше или равно \(1\,000\,000\), то сначала произносится число миллионов в мужском роде, затем слово «миллион», «миллиона» или «миллионов», по следующим правилам. Если число миллионов, взятое по модулю 100, не равно 11 и дает остаток 1 по модулю 10, то произносится слово «миллион». Если число миллионов, взятое по модулю 100, не равно 12, 13 или 14 и дает остаток 2, 3 или 4 по модулю 10, то произносится слово «миллиона». Иначе произносится слово «миллионов».
Если число по модулю \(1\,000\,000\) больше или равно \(1\,000\), то затем произносится число тысяч в женском роде, затем слово «тысяча», «тысячи» или «тысяч», по следующим правилам. Если число тысяч, взятое по модулю 100, не равно 11 и дает остаток 1 по модулю 10, то произносится слово «тысяча». Если число тысяч, взятое по модулю 100, не равно 12, 13 или 14 и дает остаток 2, 3 или 4 по модулю 10, то произносится слово «тысячи». Иначе произносится слово «тысяч».
Затем, если число по модулю \(1\,000\) отлично от нуля, в мужском роде произносится число единиц.
Например, число \(978\,121\,014\) произносится как «девятьсот семьдесят восемь миллионов сто двадцать одна тысяча четырнадцать», а число \(1\,000\,142\) как «один миллион сто сорок два». Заметим, что перед словом «миллион» нельзя опускать слово «один», перед словом «тысяча» слово «одна», а числа от \(11\) до \(19\) произносятся одним словом.
Помогите Васе найти все телефонные номера, которые произносятся так же, как тот, который он записал.
На входе единственная строка, содержащая номер записанного Васей телефона. Номер телефона --- это целые числа, разделенные символом «-» (ASCII код 39). Каждое число в записи положительно, содержит не более девяти цифр и не содержит ведущих нулей. Гарантируется, что в записанном Васей номере встречается не больше 50 цифр.
В первой строке выведите количество телефонных номеров, которые читаются так же, как и записанный Васей номер. В следующих строках выведите эти номера телефонов. Каждый номер должен находиться в отдельной строке. Каждый номер должен состоять из чисел от 1 до \(999\,999\,999\), разделенных дефисами.
Порядок телефонов в ответе не важен. Гарантируется, что количество номеров в ответе не превышает \(100\,000\). Учтите, что в ответе могут встречаться и номера, составленные более чем из 50 цифр.
3000-101
4 3000-100-1 3000-101 3100-1 3101
На Всероссийскую командную олимпиаду школьников по программированию приезжает множество делегаций из различных городов нашей страны. Расселить делегации по номерам в гостинице является непростой задачей.
Из одного крупного города приехала делегация, состоящая из \(n\) человек. В гостинице, куда решено было заселить делегацию, имеются лишь двухместные и трехместные номера. Для экономии средств делегация хочет занять как можно меньше номеров, при этом в занимаемых номерах не должно оставаться свободных мест.
Помогите определить, каким образом можно разместить делегацию из \(n\) в двухместных и трехместных номерах, чтобы использовать суммарно минимальное число номеров.
В входном файле содержится единственное целое число \(n\) (\(2 \le n \le 100\)) --- размер делегации.
В выходной файл выведите два целых числа \(a_2\) и \(a_3\), разделенных пробелом --- число двухместных и трехместных номеров, которые необходимо выделить делегации, соответственно.
7
2 1
Генералу Тупикову пришла в голову гениальная идея эффектного шоу во время проведения парада в честь пятидесятилетия победы в маленькой победоносной войне Флатландии над Берляндией.
В параде примет участие \(n\) солдат. Солдаты, выстроенные в колонну по одному, выйдут на главную площадь. Затем, по команде генерала, некоторые солдаты сделают шаг влево, а остальные солдаты --- шаг вправо. В результате солдаты, сделавшие шаг влево, должны оказаться упорядочены по возрастанию роста, а сделавшие шаг вправо --- по убыванию.
Генерал приказал немедленно принести ему список солдат, которые примут участие в параде, чтобы определить, в каком порядке им следует построиться, кому сделать шаг влево, а кому --- вправо. Однако выяснилось, что репетиции парада продолжаются уже несколько месяцев и солдаты знают, в каком порядке они должны выйти на площадь.
Эта новость слегка огорчила генерала, но он не упал духом. Он выяснил рост всех солдат, которые примут участие в параде, и теперь хочет разбить всех солдат на два непустых множества: тех кто сделает шаг влево и тех, кто сделает шаг вправо. Сделавшие шаг влево должны оказаться упорядочены по возрастанию роста, а сделавшие шаг вправо --- по убыванию.
Помогите генералу составить сценарий парада, выясните, кому из солдат надо отдать команду сделать шаг влево. Остальные солдаты сделают шаг вправо. Хотя бы один солдат должен сделать шаг влево, и хотя бы один солдат должен сделать шаг вправо.
В первой строке входного файла задано целое число \(n\) (\(2 \le n \le 100\,000\)) --- количество солдат. Во второй строке задано \(n\) целых положительных чисел \(a_1, a_2, \ldots, a_n\) --- рост солдат (\(1 \le a_i \le 10^9\)). Рост солдат приведен в порядке, в котором они выйдут на площадь.
В первой строке выходного файла выведите \(k\) --- количество солдат, которым надо сделать шаг влево (\(1 \le k \le n - 1\)). В второй строке выходного файла выведите \(k\) целых чисел \(b_1, b_2, \ldots, b_k\) --- номера солдат, которым надо сделать шаг влево (\(1 \le b_1 < b_2 < \ldots < b_k \le n\)).
Рост этих солдат должен строго возрастать, а рост оставшихся солдат должен строго убывать. Если решений несколько, выведите любое.
В случае, если решения нет, в единственной строке выходного файла выведите «Impossible».
6 6 1 4 3 2 5
3 2 4 6
6 1 3 2 4 6 5
Impossible
3 1 1 1
Impossible