Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 8 задач <---
Источники --> Командные олимпиады --> Кировские командные турниры
    2001(8 задач)
Страница: << 1 2 Отображать по:
#1133
Васины очки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо определить, сколькими способами можно представить число Y-X в виде суммы чисел A и C (порядок слагаемых не учитывается).

«Что наша жизнь? Игра!»

Вася в казино играет в интересную игру.

Сначала он платит вступительный взнос за игру и в обмен на деньги получает право играть. Более того, за уплаченные деньги он сразу получает X очков.

На автомате, в который он играет, есть три кнопки. Когда он нажимает первую, к его очкам добавляется A очков. Когда нажимает вторую — добавляется B. Когда нажимает третью — добавляется C очков.

Ему разрешается сначала несколько раз (или ни разу) нажать третью кнопку, и затем несколько раз (или ни разу) — первую. Нажимать вторую кнопку Васе запрещено.

Если после этого он набрал ровно Y очков, то Вася считается выигравшим, и ему выплачивается премия. Если же Y очков набрать не удается, Вася считается проигравшим, и ничего не получает.

Если Вася выиграл, то считается, что он разгадал одну из волшебных последовательностей нажатий, которые приводят к выигрышу. Он имеет право и дальше играть в эту игру, и искать другие такие последовательности, которые X очков превращают в Y, но ему категорически запрещено использовать одну и ту же выигрышную последовательность более одного раза.

Напишите программу, которая посчитает, сколько различных выигрышных последовательностей существует, то есть сколько раз Вася может выиграть в эту замечательную игру.

Входные данные

Во входном файле записаны числа X, A, B, C, Y. Каждое из этих чисел — целое из диапазона [–109, 109].

Выходные данные

В выходной файл выведите одно число — количество различный выигрышных последовательностей. Если таких последовательностей бесконечно много, выведите –1.

Примеры
Входные данные
0 0 -1 0 1
Выходные данные
0
#1134
РЛС
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Задана карта района, на которой присутствуют не более 5 связных фигур из клеток. Необходимо окружить все клетки забором минимальной длины (при этом группы клеток можно окружать отдельным забором).

Задачи противовоздушной обороны: ...борьба с десантом на всем маршруте пролета,

уничтожение вертолетов огневой поддержки, действующих из засады»

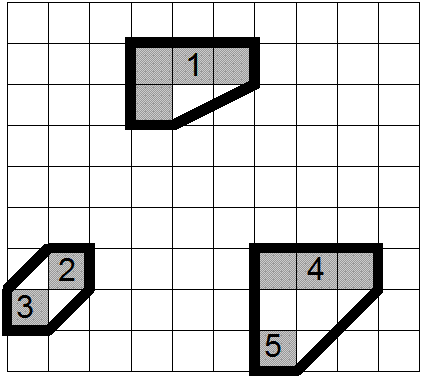Радиолокационная станция (РЛС) состоит из нескольких передатчиков (не более 5). К сожалению, их нельзя ставить рядом — они друг для друга создают помехи. Каждый передатчик состоит из квадратных модулей, которые располагаются вплотную друг к другу.

Вам дана карта района, в котором расположена РЛС. Вся карта для удобства разбита на квадраты, и для каждого квадрата известно, располагается в нем какой-то из модулей одного из передатчиков РЛС или нет.

Требуется оградить забором (или несколькими заборами) минимально возможной суммарной длины все передатчики РЛС. Забор — это произвольная ломаная (ее элементы не обязаны идти по сторонам клеток). Одним забором могут быть огорожены сразу несколько передатчиков.

Входные данные

Во входном файле записаны два числа N и M, задающие размеры района, в котором расположена РЛС (1N20, 1M20). Далее идет N строк, по M чисел в каждой, задающих карту района. Каждое из этих чисел 0 или 1 — 1 означает, что в этом квадрате находится один из модулей передатчика РЛС, а 0 — что в этом квадрате ничего ценного нет.

Общее количество передатчиков РЛС не превышает 5. Каждый передатчик — это связанная группа модулей (модули называются связанными, если они располагаются в квадратах карты, у которых есть общая граница, либо связаны через какие-то другие модули).

Ограничения на число модулей нет.

Выходные данные

В выходной файл выведите одно число — минимально возможную длину забора с тремя значащими цифрами после точки.

Примеры
Входные данные
2 2
1 0
0 1
Выходные данные
6.828
Входные данные
4 5
1 0 0 0 1
0 0 0 0 0
0 0 1 0 0
1 0 0 0 1
Выходные данные
18.000
#1135
Гипер-каналы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо найти кратчайший путь в невзвешенном графе. Вершины задаются парой чисел.

«Не плюй в телепорт: вылетит — не поймаешь!»

На зараженной радиацией планете некоторые точки соединены между собой гипер-каналами. Когда человек заходит в гипер-канал в одной точке, он мгновенно оказывается в другой. Все гипер-каналы двусторонние — то есть их можно использовать для перемещения в обоих направлениях (как из первой точки во вторую, так и из второй в первую).

К сожалению, гипер-каналы платные — каждый проход через гипер-канал стоит 10 у.е.

Перемещаться по поверхности планеты из одной точки в другую, не используя гипер-каналы, чревато для здоровья (радиация, однако!).

Напишите программу, которая определит, какой минимальной суммой у.е. должен располагать путешественник, чтобы добраться из одной точки в другую, не рискуя своим здоровьем.

Входные данные

Во входном файле записаны сначала два числа — начальные координаты расположения путешественника, затем еще два числа — координаты точки, куда ему надо попасть. Затем записано число N — количество гипер-каналов на планете (0N500). Затем идет N описаний гипер-каналов. Каждый гипер-канал описывается четверкой чисел. Первые два задают координаты одной из соединяемых гипер-каналом точек, последние два — координаты другой. Все координаты — целые числа, не превышающие по модулю 1000000.

Выходные данные

В выходной файл запишите одно число — минимальную сумму, которой должен располагать путешественник для достижения цели. Если, не рискуя здоровьем, он не сможет добраться до конечной точки, запишите в выходной файл число 171717 (столько стоит лечение лучевой болезни на этой планете).

Примеры
Входные данные
10 10
-10 -10
3
-10 -10 -10 -10
-10 -10 1 1
10 10 1 1
Выходные данные
20
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест