Привидение Петя любит играть со своими кубиками. Он любит выкладывать их в ряд и разглядывать свое творение. Однако недавно друзья решили подшутить над Петей и поставили в его игровой комнате зеркало. Ведь всем известно, что привидения не отражаются в зеркале! А кубики отражаются. Теперь Петя видит перед собой N цветных кубиков, но не знает, какие из этих кубиков настоящие, а какие — всего лишь отражение в зеркале. Помогите Пете! Выясните, сколько кубиков может быть у Пети. Петя видит отражение всех кубиков в зеркале и часть кубиков, которая находится перед ним. Часть кубиков может быть позади Пети, их он не видит.
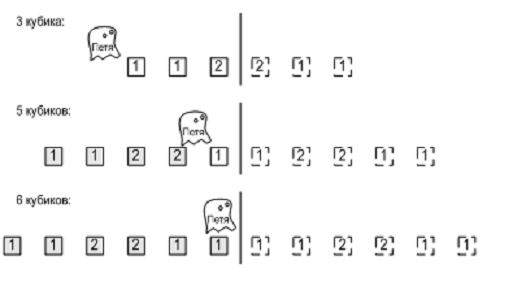
Первая строка входного файла содержит число N ( 1 ≤ N ≤ 1000000 ) и количество различных цветов, в которые могут быть раскрашены кубики — M ( 1 ≤ M ≤ 1000000 ). Следующая строка содержит N целых чисел от 1 до M — цвета кубиков.
Выведите в выходной файл все такие K , что у Пети может быть K кубиков
6 2 1 1 2 2 1 1
3 5 6
Известно, что в солнечной системе есть 8 планет и один планетоид. Мало кто знает, что ещё есть секретная планета, населенная медведями. Именно туда ассоциация Savez отправляет бравого генерала Хенрика для изучения медведей. Выяснилось, что медведи умеют телепортироваться. Расчётливый генерал Хедрик решил завербовать их в свою армию.
У одного медведя есть N строк (обозначим i -ю из них x i ). Исследования показывают, что количество раз, которое может телепортироваться медведь равно длине наибольшей подпоследовательности этих строк, удовлетворяющей такому правилу: строки x i и x j ( i < j ) могут принадлежать одной такой последовательности, если x i является и префиксом, и суффиксом x j .
Помогите уставшему от долгого полёта генералу Хендрику определить, сколько телепортаций сможет сделать данный медведь.
В первой строке содержится одно целое число N – количество строк, которые есть у медведя. В последующих N строках содержатся сами эти строки. Входной файл содержит не более двух миллионов символов.
Выведите одно число – ответ на вопрос любопытного генерала Хендрика.
В первом примере наибольшая последовательность A -> AA -> AAA В третьем примере наибольшая последовательность A -> A -> A или B -> B -> B
5 A B AA BBB AAA
3
5 A ABA BBB ABABA AAAAAB
3
6 A B A B A B
3
Строка \(s\) назывется префиксом строки \(t\), если строка \(t\) начинается со строки \(s\). Строка \(s\) назывется суффиксом строки \(t\), если строка \(t\) заканчивается на строку \(s\).
Назовём две строки \(s\) и \(t\) циклически эквивалентными, если существует циклический сдвиг, переводящий строку \(s\) в строку \(t\); другими словами строки \(s\) и \(t\) циклически эквивалентны тогда и только тогда, когда, строка \(s\) может быть получена из строки \(t\) путем перемещения некого суффикса строки \(t\) в начало строки \(t\). Например, строки \(ababba\) и \(abbaab\) циклически эквивалентны, в то время как строки \(ababba\) и \(ababab\) нет. В частности, любая строка циклически эквивалентна самой себе.
Дана строка \(t\) длины \(n\). Требуется найти такой префикс \(p\) и такой суффикс \(s\) строки \(t\), что:
- \(p\) циклически эквивалентен \(s\) (и, как следствие, их длины равны)
- длина \(p\) не превосходит \(\frac{n}{2}\) (то есть \(p\) и \(s\) не пересекаются в \(t\))
- длина \(p\) максимальна
Первая строка входных данных содержит одно целое число \(n\) — длину строки \(е\) (\(1 \le n \le 1000 000\)).
Вторая строка входных данных содержит строку \(t\) состоящую из строчных латинких букв.
Выведите единственное целое число \(res\) - наибольшее целое число, такое что (\(0 \le res \le \frac{n}{2}\)) и \(res\) - ый префикс строки \(t\) циклически эквивалентен \(res\)-му суффиксу строки \(t\).
В тестах суммарной стоимостью не менее \(30\) баллов дополнительно гарантируется что \(n \le 500\).
В тестах суммарной стоимостью не менее \(50\) баллов дополнительно гарантируется что \(n \le 5000\).
В тестах суммарной стоимостью не менее \(80\) баллов дополнительно гарантируется что \(n \le 200000\).
В тестах суммарной стоимостью не менее \(90\) баллов дополнительно гарантируется что \(n \le 500000\).
15 ababbabababbaab
6
В рамках новой рекламной кампании некоторая корпорация хочет разместить свой логотип где-нибудь в городе. Компания собирается потратить весь рекламный бюджет на логотип, поэтому он должен быть воистину огромным. Один из менеджеров решил использовать здания целиком как части логотипа.
Логотип состоит из \(n\) вертикальных полос различной высоты. Полосы пронумерованы от \(1\) до \(n\) слева направо. Логотип описывается перестановкой \((s_1, s_2, ..., s_n)\) чисел \(1, 2, ..., n\). Полоса с номером \(s_1\) - самая низкая, полоса с номером \(s_2\) - следующая по высоте и, наконец, полоса \(s_n\) - самая высокая. Фактическая высота полос не имеет большого значения. Вдоль главной улицы расположено \(m\) зданий. К вашему удивлению, высота зданий различна. Задача состоит в том, чтобы найти все позиции, на которых логотип соответствует зданиям. Помогите компании и найдите все непрерывные последовательности зданий, которые соответствуют логотипу. Непрерывная последовательность зданий соответствует логотипу, если здание \(s_1\) в этой последовательности является самым низким, здание \(s_2\) является следующим по высоте и т. д. Например, последовательность зданий высотой \(5, 10, 4\) соответствует логотипу, описанному перестановкой \((3, 1, 2)\), поскольку здание №3 (высотой 4) является самым низким, здание №1 - вторым по высоте, а здание №2 - самым высоким.
Первая строка стандартного ввода содержит два целых числа \(n\) и \(m\) \((2 \le n \le m \le 1 000 000)\).
Вторая строка содержит \(n\) целых чисел \(s_i\), образующих перестановку чисел \(1, 2, ..., n\). То есть \(1 \le s_i \le n\) и s\(_i \neq s_j\) для \(i \neq j\).
Третья строка содержит \(m\) целых чисел \(h_i\) - высоты зданий (\(1 \le h_i \le 10^9\) для \(1 \le i \le m\)). Все числа различные.
В каждой строке числа разделены пробелами.
Первая строка стандартного вывода должна содержать целое число \(k\) – количество совпадений.
Вторая строка должна содержать \(k\) целых чисел - индексы зданий начиная с 1, которые соответствуют первой полосе из логотипа в правильном соответствии. Числа должны быть перечислены в возрастающем порядке.
Если \(k = 0\), ваша программа должна напечатать пустую вторую строку.
В тестах суммарной стоимостью не менее 35 баллов \(n \le 5000\) и \(m \le 20 000\).
В тестах суммарной стоимостью не менее 60 баллов \(n \le 50 000\) и \(m \le 200 000\).
5 10 2 1 5 3 4 5 6 3 8 12 7 1 10 11 9
2 2 6
Байтазар, король Байтотии организовал масштабную реформу имён своих подданных. Имена жителей Байтотии исторически часто содержат повторяющиеся фразы и Байтазар хочет с одной стороны упростить имена, а с другой, сохранить традиции повторения, а именно Байтазар хочет заменить каждое из имён в Байтотии на имя такой же длины, чтобы при этом множества периодов для старого и нового имён совпали, но имя при этом состояло только из символов «0» и «1». Из всех кандидатов в новое имя Байтазар хочет выбрать лексикографически минимальное.
Натуральное число \(k\) (\(1 \le k \lt n\)) называется периодом строки \(s\) длины \(n\) тогда и только тогда, когда для любого натурального \(i\), такого что \(1 \le i \le n - k\), верно что \(s_i = s_{i + k}\).
Множество периодов для данной строки \(s\) – множество таких чисел \(i\), что \(i\) является периодом \(s\). Обозначим его за Per(\(s\)). К примеру, Per(«ABIABUABIAB») = {6, 9}, Per(«0000») = {1, 2, 3}.
Помогите Байтазару перевести имена его подданных, и, возможно, он разрешит вам сохранить ваше собственное имя!
В первой строке ввода дано единственное число \(t\) (\(1 \le t \le 20\)) - количество имён, которые необходимо перевести в соответсвии с реформой Байтазара.
В последующих \(t\) строках содержатся имена жителей Байтотии. В \(i\) строке содержится строка \(s_i\), состоящяя из заглавных латинских букв - имя \(i\) жителя до перевода.
Вы должны вывесте \(t\) строк. В \(i\) строке выведите имя, в которое превратится имя \(s_i\) после перевода.
Подзадача 1 (30 баллов): длина каждого имени не превосходит 20 (\(|s_i| \le 20\))
Подзадача 2 (70 баллов): длина каждого имени не превосходит 200000 (\(|s_i| \le 200000\))
3 ABIABUABIAB BABBAB BABURBAB
01001101001 010010 01000010