При написании программы, проверяющей ответ участника для задачи 3204 "Отрезки на прямой возвращаются" (ссылка на задачу) (прочитайте её условие!), жюри столкнулось с трудностями, превосходящими сложность самой задачи. С мыслью "почему бы и нет" написание такой программы было решено также включить в комплект задач.
Проверяющей программе доступно три блока информации:
- входные данные в формате, описанном в условии предыдущей задачи,
- ответ некоторого абстрактного участника в формате, также описанном в предыдущем условии,
- ответ жюри.
Ваша задача - написать программу, которая по этим данным определит, правильно ли программа абстрактного участника посчитала ответ.
Вход состоит из трёх частей. Первая часть - число \(N\) (\(1 \le N \le 100\,000\)) и следом \(N\) пар \(a_i\), \(b_i\) (\(-10^9 \le a_i \lt b_i \le 10^9\)). Далее идут \(N\) чисел, каждое из которых от 0 до \(N\), \(i\)-е равно номеру отрезка, являющегося одним из непосредственно содержащих \(i\)-й, либо нулю - по мнению абстрактного участника. Далее идут ещё \(N\) чисел в том же формате - ответ жюри на эту задачу.
Входные данные всегда корректны. Это означает, например, что ответ участника не нужно проверять на соответствие формату и что ответ жюри точно правильный.
Выведите \(N\) строк. В \(i\)-й строке должен быть вердикт для \(i\)-го отрезка. Выведите OK, если ответ абстрактного участника правильный, и WA - иначе.
Тесты состоят из четырёх групп.
- Тест 1, из условия, оценивается в 0 баллов.
- Тесты 2--11. В них \(N \le 100\). Группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- Тесты 12--27. В них \(N \le 10\,000\). Группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- Тесты 28--35. Полные ограничения. Каждый тест оценивается в 5 баллов (тесты оцениваются независимо друг от друга). При этом баллы за тесты этой группы ставятся только тогда, когда программа проходит все тесты групп 1 и 2. Если программа не проходит хотя бы один из тестов групп 1 и 2, то баллы за тесты группы 3 не ставятся.
4 2 3 0 4 1 6 0 5 2 2 1 0 3 4 0 0
OK WA WA OK
Прямоугольная детская площадка полностью замощена \(N\) плитками. Все плитки прямоугольные, возможно разного размера. Плитки не перекрываются.
На этой площадке решили построить песочницу. Чтобы подготовить место для песочницы, необходимо вынуть не более K плиток таким образом, чтобы песочница занимала все освободившееся пространство, была прямоугольной и имела максимально возможную площадь.
Напишите программу, которая определяет расположение песочницы, удовлетворяющей перечисленным выше требованиям.
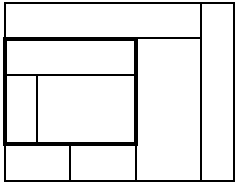
Введем систему координат так, чтобы начало координат совпадало с одним из углов площадки, а оси координат шли вдоль сторон площадки. В этом случае противоположный угол площадки окажется в точке \((X,Y)\).
Первая строка содержит два числа \(X\) и \(Y\) (натуральные числа, не превышающие 10000). Во второй строке заданы числа \(N\) и \(K (1 \le K \le N \le 2000)\). Следующие \(N\) строк файла содержат по четыре целых числа \(X_{i,1}, Y_{i,1}, X_{i,2}, Y_{i,2}\), задающих координаты двух противоположных углов плитки.
Выведите координаты двух противоположных углов найденного прямоугольника. Если решений несколько, выведите любое из них.
В этой задаче 16 тестов, каждый тест оценивается независимо.
Гарантируется, что решения, корректно работающие при \(n \le 25\) наберут не менее 30 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 500\) наберут не менее 42 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 1500\) наберут не менее 54 баллов.
7 5 8 3 0 0 2 1 2 0 4 1 0 1 1 3 1 1 4 3 0 3 4 4 0 4 6 5 4 0 6 4 6 0 7 5
0 1 4 4
В супермаркете «На троечку» часто происходят распродажи товаров, срок годности которых подходит к концу. Каждый товар привозят в магазин в определенное время, а через некоторое его вывозят из магазина, в связи с окончанием срока годности. Более формально, каждый товар имеет стоимость c i , время его завоза в магазин a i и время его вывоза из магазина b i .
У Иннокентия есть хитрый план похода в магазин. Даже несколько. Каждый план похода в магазин выглядит так: Иннокентий выбирает какое-то время, когда он появится в магазине m j , время s j , которое он проведет в магазине среди огромных стеллажей товаров, и сумму денег k j , которую он рассчитывает потратить. Для каждого плана он хочет узнать, сможет ли он осуществить его, т. е. верно ли, что он сможет во время своего пребывания в магазине купить несколько товаров суммарной стоимостью ровно k j , при этом все выбранные товары должны быть в магазине на протяжении всего пребывания Иннокентия в магазине.
Помогите Иннокентию определить, какие из его планов можно выполнить.
В первой строке входных данных содержится число N — общее количество товаров в магазине ( 1 ≤ N ≤ 500 ). Далее содержатся описания товаров, каждый товар описывается тремя целыми числами c i , a i , b i , обозначающими стоимость товара, время его завоза и время его вывоза из магазина ( 1 ≤ c i ≤ 1 000 , 1 ≤ a i < b i ≤ 10 9 ).
Далее содержится число M — количество планов Иннокентия ( 1 ≤ M ≤ 500 000 ). Каждый план описывается тремя целыми числами m j , k j , s j , обозначающими время прихода Иннокентия в магазин, сумму денег, которую он готов потратить в этом плане и длительность его пребывания в магазине ( 1 ≤ m j ≤ 10 9 , 1 ≤ k j ≤ 100 000 , 0 ≤ s j ≤ 10 9 ).
Помните, что это только планы, т. е. ситуация в магазине не меняется вне зависимости от того, может ли Иннокентий осуществить план или нет.
Для каждого плана в отдельной строке выведите « YES », если Иннокентий может его осуществить, и « NO » в противном случае.
Тесты к этой задаче состоят из четырех групп.
- Тест 1. Тест из условия, оценивается в ноль баллов.
- Тесты 2–7. В тестах этой группы M ≤ 10 , a i , b i , m j , s j ≤ 20 000 , k j ≤ 1 000 . Эта группа оценивается в 30 баллов.
- Тесты 8–11. В тестах этой группы N ≤ 200 , M ≤ 200 , k j ≤ 5 000 . Эта группа оценивается в 30 баллов.
- Тесты 12–23. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы.
5 6 2 7 5 4 9 1 2 4 2 5 8 1 3 9 5 2 7 1 2 7 2 3 2 0 5 7 2 4 1 5
YES NO YES YES NO
Королевские Железные Дороги (КЖД) готовятся открыть новый, скоростной, маршрут из столицы в соседний город NN и обратно. Новые поезда будут добираться до места назначения втрое быстрее обычных ночных поездов. Конкурс на поставку новых составов выиграла зарубежная компания «MacroHard» — производитель локомотивов «Hawk», которые будут использоваться в королевстве под локализованным названием «Ястреб». Расписание уже готово, но до сих пор не решен вопрос, сколько именно составов нужно, чтобы его выполнить. Не требуется покупать по составу на каждый рейс, поскольку поезд, прибывший на станцию, может выполнить и обратный рейс. КЖД обратились к вам и просят написать программу, способную рассчитать минимально необходимое количество поездов на один день. Расписание состоит из N 1 рейсов из столицы в город NN и N 2 обратных рейсов. Для каждого рейса известно время отправления и время прибытия — с точностью до минуты. Любой рейс полностью выполняется в течение одних календарных суток (с 00: 00 до 23: 59 включительно) — то есть никакой рейс не прибывает на следующий день после отправления. Каждый рейс занимает как минимум одну минуту, то есть ни один поезд не прибывает на станцию назначения в ту же минуту, в которую он отправился . КЖД настолько эффективны, что после прибытия поезд готов в ту же минуту отправиться в обратный рейс. Одновременно на станции может находиться, отправляться или прибывать любое количество поездов. Руководство КЖД не одобряет холостые поездки, поэтому поезда не могут перемещаться вне расписания в течение дня. Отметим, что вам не нужно учитывать подготовку к выполнению расписания следующего дня — к моменту начала следующих суток железнодорожники способны обеспечить любое распределение составов по станциям, независимо от того, как они были распределены к концу предыдущих.
В первой строке находится число N 1 (1 ≤ N 1 ≤ 100000) — количество рейсов из столицы в город NN. В следующих N 1 строках находятся описания рейсов, по одному на строке: время прибытия и время отправления, разделенные дефисом («-»). И время прибытия, и время отправления записаны в формате HH : MM ,где HH — час (число от 0 до 23, при необходимости, дополненное ведущим нулем до двух цифр), MM — минута (число от 0 до 59, при необходимости, дополненное ведущим нулем до двух цифр). В N 1 + 2 - й строке находится число N 2 (1 ≤ N 2 ≤ 100000) — количество обратных рейсов: из города NN в столицу. На следующих N 2 строках находятся описания этих рейсов в том же формате.
Выведите единственное число — минимально возможное количество составов, которое нужно для выполнения расписания.
В первом примере семь поездов могут выполнить рейсы, например, следующим образом: 1. обратно 6:35, туда 19:00
2. туда 6:45, обратно 11:00
3. обратно 7:15, туда 20:08
4. туда 7:36, обратно 15:40
5. обратно 14:00
6. обратно 18:35
7. обратно 20:20.
Во втором примере один поезд может выполнить все рейсы.
4 06:45-10:20 07:36-11:26 19:00-22:35 20:08-23:58 7 06:35-10:10 07:15-11:10 11:00-14:48 14:00-17:48 15:40-19:28 18:35-22:23 20:20-23:55
7
2 10:00-12:00 15:00-17:00 2 12:30-14:30 17:30-19:30
1