Страница: 1 Отображать по:
#111426
Раздел имущества
  
Темы: [meet in the middle]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В этой задаче входные данные записаны в файле exchange.in, вывод нужно записать в файл exchange.out.

Вася — профессиональный юрист, и сейчас он рассматривает очередное дело о разделе имущества. Всего имеется N наследников, каждый из них имеет значимость Ri. Богатый дедушка оставил им состояние в размере L иностранных тугриков. Логично раздать наследство пропорционально значимости, в этом случае i-ый наследник получит 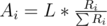иностранных тугриков. Однако, наследники очень привередливы, поэтому наследник желает получить кругленькую сумму, т.е. ту, которая делится на Si.

Чтобы выполнить просьбу наследников, Вася может округлять числа Ai до ближайшего, делящегося на Si (в случае, если делимость не имеет места). При этом, Вася сам выбирает, округлить очередное число вниз или вверх. Пусть Bi означает, сколько в итоге получит очередной наследник. Так как Вася — честный человек, он хочет минимизировать 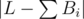. В случае нескольких вариантов, он выбирает тот, при котором 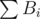будет наименьшей.

Входные данные

В первой строке входных данных содержится два целых числа N и L — количество наследников и размер состояния, соответственно (1 ≤ N ≤ 30, 1 ≤ L ≤ 109). В следующей строке содержатся значимости наследников Ri (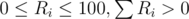). В следующей строк содержатся числа Si (1 ≤ Si ≤ 109).

Выходные данные

Выведите единственное число — искомую оптимальную сумму .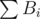

Примеры тестов

Входные данные
2 250
1 2
100 150
Выходные данные
250
Входные данные
3 1000
25 25 50
34 77 52
Выходные данные
989
Входные данные
3 10
1 1 0
50 50 50
Выходные данные
0

#113570
День рождения Мирко
  
Источники: [ Личные олимпиады, COCI, COCI 2015-2016, Раунд 3, День рождения Мирко ]
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
512 megabytes

Мирко получил в подарок на свой день рождения квадратный стол N x N , где в каждой клетке записано неотрицательное целое число. К сожалению, некоторые числа кажутся Мирко слишком большими, поэтому он собирается положить на стол K фишек домино, которые закроют некоторые слишком большие числа. Точнее, он собирается положить фишки домино в соответствии со следующими правилами:

1. Каждая фишка домино покрывает две клетки, соседних по строчке или столбцу..

2. Фишки домино не накладываются друг на друга (но могут соприкасаться).

3. Сумма чисел на всех видимых (непокрытых) клетках минимальна.

Ваша задача - определить минимально возможную сумму чисел на видимых клетках. Тесты к задаче таковы, что на поле всегда можно положить K не накладывающихся друг на друга фишек домино.

Входные данные

Первая строка содержит два целых числа: N ( 1 ≤ N ≤ 2000 ) - размер стола, и K ( 1 ≤ K ≤ 8 ) - количество фишек домино. Каждая из следующих N строк содержит N целых чисел (в диапазоне [0, 1000]) - числа в соответствующих клетках поля.

Выходные данные

Выведите единственное целое число - минимально возможную сумму чисел в клетках после установки фишек домино.

Примечание

Решения, работающие при K ≤ 5 , будут оцениваться в 70 баллов.

Примеры
Входные данные
3 1
2 7 6
9 5 1
4 3 8
Выходные данные
31
Входные данные
4 2
1 2 4 0
4 0 5 4
0 3 5 1
1 0 4 1
Выходные данные
17
#113809
Простыни
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

В один прекрасный день маленький Дональд решил вымыть N своих чистых белых простыней. После мытья он положил их на землю во дворе, чтобы их высушить. Дональд помещал простыни так, чтобы никакие две простыни не касались ни сторонами, ни углами, и чтобы их стороны не пересекалась, но возможно, что он разместил меньшие простыни поверх более крупных или что простыня полностью закрывает какие-то другие простыни. Сделав это, Дональд лег спать.

Друг Дональда Ким как-то узнал о том, что Дональд сушит простыни и решил пообщаться с ним. Он нашел пейнтбольный пистолет своего отца на чердаке. Наряду с пистолетом у него было несколько пейнтбольных мячей, каждый из них имел свой цвет (не обязательно уникальный). Как только Дональд заснул, Ким вошёл во двор к Дональду и начал стрелять пр простыням из пейнтбольного пистолета. Простыни Дональда очень тонкие, поэтому, когда Ким попадает в какую-то простыню, она пропускает краску дальше, на простыню ниже (и та тоже, и так происходит, пока не закончатся простыни и краска не попадет на землю). После того, как Ким использовал все шары, он с радостью покинул двор Дональда. Дональд был очень расстроен, увидев, что случилось с его простынями. Дональд очень заинтересован в правильных данных о преступлении Кима, но он в шоке и не способен думать, поэтому просит вас сказать ему количество цветов на каждой простыне.

Мы можем представлять двор Дональда как бесконечную систему координат, а простыни - как прямоугольники, параллельные осям координат. Выстрелы Кима могут быть представлены как точки в этой системе.

Когда-то в детстве дедушка рассказал Киму, что снаряд никогда не попадает в одну воронку дважды, так что координаты всех выстрелов попарно различны.

Входные данные

Первая строка ввода содержит два числа - количество простынь N ( 1 ≤ N ≤ 80000 ), и количество шаров M ( 1 ≤ M ≤ 80 000 ).

i -я из следующих N строк содержит четыре числа: координаты нижнего левого угла A i , B i ( 1 ≤ A i , B i ≤ 10 9 ) и верхнего правого угла C i , D i , ( 1 ≤ C i , D i ≤ 10 9 ) i -й простыни.

j -я из следующих M строк содержит три числа, где X j , Y j ( 1 ≤ X j , Y j ≤ 10 9 ) - координаты j -го выстрела Кима и K j ( 1 ≤ K j ≤ 10 9 ) - цвет j -го пейнтбольного шара.

Выходные данные

i -я из N выходных строк должна содержать количество цветов на i -м листе.

Система оценки

Тесты к данной задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп.

Примеры
Входные данные
2 2
1 1 3 3
5 6 10 10
3 3 1
5 1 2
Выходные данные
1
0
Входные данные
3 3
1 1 7 7
2 2 6 6
3 3 5 5
4 4 1
2 6 2
4 7 3
Выходные данные
3
2
1
Входные данные
1 3
1 1 7 7
2 6 2
4 7 3
4 4 1
Выходные данные
3
#113813
Небоскрёбы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Вы когда-нибудь мечтали стать главным героем компьютерной игры? Главный герой этой истории, Бранимир, мечтает сейчас именно об этом.

Мир в мечте Бранимира состоит из N небоскребов, пронумерованных слева направо. Для i -го небоскреба, известна его высота H i и количество золотых монет G i на крыше этого небоскреба. Игра начинается с прыжка на любой из небоскребов и состоит из нескольких ходов. На каждом ходу Бранимир может прыгнуть на любой небоскрёб, находящийся справа от него, но так, чтобы высота нового небоскрёба была не меньше того небоскрёба, на котором сейчас сидит Бранимир. Оказавшись на крыше небоскреба, Бранимир собирает все золотые монеты на ней. Бранимир может закончить игру после любого количества шагов (возможно, нулевого), но он должен собрать не менее K золотых монет, чтобы перейти на следующий уровень.

Бранимир хочет узнать, сколько существует способов сыграть в эту игру так, чтобы перейти на следующий уровень. Две игры называются разными, если существует небоскреб который был посещен в одной игре, но не был посещён в другой.

Входные данные

Первая строка содержит 2 натуральных числа N и K ( 1 ≤ N ≤ 40 , 1 ≤ K ≤ 4·10 10 ) — число небоскрёбов и количество монет, которые надо набрать соответственно.

Следующие N строк содержат информацию о небоскрёбах. В i -й строке даны 2 числа H i и G i ( 1 ≤ H i , G i ,  ≤ 10 9 ) — высота и количество монет на i -м небоскрёбе.

Выходные данные

В единственной строке вывода выведите число возможных игр, в которых Бранимир сможет пройти на следующий уровень.

Система оценки

Решение, корректно работающее при n ≤ 20 будет оцениваться в 40 баллов.

Примеры
Входные данные
4 6
2 1
6 3
7 2
5 6
Выходные данные
3
Входные данные
2 7
4 6
3 5
Выходные данные
0
Входные данные
4 15
5 5
5 12
6 10
2 1
Выходные данные
4
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест