Страница: 1 2 3 4 5 6 7 >> Отображать по:
#11
Казино
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Вновь открытое казино предложило оригинальную игру.

В начале игры крупье выставляет в ряд несколько фишек разных цветов. Кроме того, он объявляет, какие последовательности фишек игрок может забирать себе в процессе игры. Далее игрок забирает себе одну из заранее объявленных последовательностей фишек, расположенных подряд. После этого крупье сдвигает оставшиеся фишки, убирая разрыв. Затем игрок снова забирает себе одну из объявленных последовательностей и так далее. Игра продолжается до тех пор, пока игрок может забирать фишки.

Рассмотрим пример. Пусть на столе выставлен ряд фишек rrrgggbbb, и крупье объявил последовательности rg и gb. Игрок, например, может забрать фишки rg, лежащие на третьем и четвёртом местах слева. После этого крупье сдвинет фишки, и на столе получится ряд rrggbbb. Ещё дважды забрав фишки rg, игрок добьётся того, что на столе останутся фишки bbbи игра закончится, так как игроку больше нечего забрать со стола. Игрок мог бы действовать и по-другому — на втором и третьем ходах забрать не последовательности rg, а последовательности gb. Тогда на столе остались бы фишки rrb. Аналогично, игрок мог бы добиться того, чтобы в конце остались ряды rrr или rbb.

После окончания игры полученные фишки игрок меняет на деньги. Цена фишки зависит от её цвета.

Требуется написать программу, определяющую максимальную сумму, которую сможет получить игрок.

Входные данные

В первой строке входных данных содержится число K (1 ≤ K ≤ 26) — количество цветов фишек. Каждая из следующих K строк начинается со строчной латинской буквы, обозначающей цвет. Далее в той же строке через пробел следует целое число Xi (1 ≤ Xi ≤ 150, i = 1..K) — цена фишки соответствующего цвета.

В (K+2)-ой строке описан ряд фишек, лежащих на столе в начале игры. Ряд задаетсяL строчными латинскими буквами (1 ≤ L ≤ 150), которые обозначают цвета фишек ряда.

В следующей строке содержится число N(1 ≤ N ≤ 150) — количество последовательностей, которые были объявлены крупье. В следующих N строках записаны эти последовательности. Гарантируется, что сумма длин этих N строк не превосходит 150 символов, и все они непустые.

Выходные данные

Выведите единственное целое число — максимальную сумму денег, которую может получить игрок.

Примеры
Входные данные
3
v 3
l 1
u 2
luvu
3
luv
vul
uuu
Выходные данные
6
#16
Приключение
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Теплым весенним днем группа из N школьников-программистов гуляла в окрестностях города Кисловодска. К несчастью, они набрели на большую и довольно глубокую яму. Как это случилось — непонятно, но вся компания оказалась в этой яме.

Глубина ямы равна H. Каждый школьник знает свой рост по плечи hi и длину своих рук li. Таким образом, если он, стоя на дне ямы, поднимет руки, то его ладони окажутся на высоте hi + li от уровня дна ямы. Школьники могут, вставая друг другу на плечи, образовывать вертикальную колонну. При этом любой школьник может встать на плечи любого другого школьника. Если под школьником i стоят школьники j1, j2, …, jk, то он может дотянуться до уровня hj1 + hj2 + … + hjk + hi + li.

Если школьник может дотянуться до края ямы (то есть hj1 + hj2 + … + hjk + hi + li ≥ H), то он может выбраться из нее. Выбравшиеся из ямы школьники не могут помочь оставшимся.

Найдите наибольшее количество школьников, которые смогут выбраться из ямы до прибытия помощи, и перечислите их номера.

Входные данные

В первой строке входных данных задается натуральное число N (1 ≤ N ≤ 2000) — количество школьников, попавших в яму.

Далее в N строках содержится по два целых числа: рост i-го школьника по плечи hi (1 ≤ hi ≤ 105) и длина его рук li (1 ≤ li ≤ 105).

В последней строке указано целое число — глубина ямы H (1 ≤ H ≤ 105).

Выходные данные

В первой строке выведите K — максимальное количество школьников, которые смогут выбраться из ямы. Если K > 0, то во второй строке в произвольном порядке выведите их номера, разделяя их пробелами. Школьники нумеруются с единицы в том порядке, в котором они заданы во входных данных. Если существует несколько решений, выведите любое.

Примечание

Решение, дающее правильный ответ только при N ≤ 100; H, hi, li ≤ 1000, будет оцениваться из 70 баллов.

Примеры
Входные данные
1
239 239
566
Выходные данные
0
Входные данные
3
1 2
1 2
4 1
7
Выходные данные
2
2 1
#19
Треугольная реформа
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.

Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.

Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.

Формат входных данных

В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.

Формат выходных данных

В первую строку  выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.

Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.

В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.

Если искомых разбиений несколько, выведите любое из них.

Примеры

Входные данные

Выходные данные

Рисунок к тесту

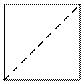
4
0 0
1 0
1 1
0 1

2
1
1 1 0 0

 1

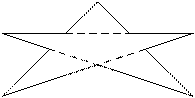
10
-6 0
0 2
6 0
3 3
6 4
2 4
0 6
-2 4
-6 4
-3 3

4
3
2 4 -2 4
0 2 3 3
-3 3 0 2

 2
#22
Ударим мостом по бездорожью
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Профиль Уральских гор задается ломаной (x1, y1), (x2, y2), …, (xN, yN), для координат вершин которой верны неравенства x1 < x2 < … < xN. Начальные и конечные точки профиля расположены на уровне моря (y1 = yN = 0).

На горном профиле заданы две различные точки A и B, между которыми требуется проложить дорогу. Эта дорога будет проходить по склонам гор и проектируемому горизонтальному мосту, длина которого не должна превышать L. Оба конца моста находятся на горном профиле. Дорога заходит на мост с одного конца и выходит с другого. Мост не может содержать точек, расположенных строго под ломаной (строительство тоннелей не предполагается).

Возможные примеры расположения моста

1

Невозможное расположение моста

2

Достоверно известно, что строительство такого моста в данной местности возможно, причем позволит сократить длину дороги из точки A в точку B. Требуется написать программу, которая определит такое расположение горизонтального моста, что длина дороги от точки A до точки B будет наименьшей.

Входные данные

Первая строка входных данных содержит два целых числа N и L — количество вершин ломаной (2 ≤ N ≤ 100 000) и максимальную длину моста (1 ≤ L ≤ 106) соответственно. Вторая строка  содержит координаты точки A, третья строка — координаты точки B. Точки A и B различны.

Последующие N строк содержат координаты вершин ломаной (x1, y1), (x2, y2), …, (xN, yN). Координаты вершин ломаной, а также точек A и B, задаются парой целых чисел, не превосходящих по абсолютному значению 106. Гарантируется, что x1 < x2 < … < xN и y1 = yN = 0, а также, что точки A и B принадлежат ломаной.

Выходные данные

В первой и второй строках выходных данных выведите координаты концов моста с точностью не менее 5 знаков после десятичной точки. В случае, когда решений несколько, выведите любое из них.

В примере в первой строке указана длина дороги от точки A до точки B с учётом построенного моста. Её не нужно выводить.

Примечание

Решения, корректно работающие при N ≤ 2000, будут оцениваться, исходя из 80 баллов.

Примеры
Входные данные
5 3
1 1
3 1
-1 0
0 2
2 0
4 2
5 0
Выходные данные
2.000000000
1.00000 1.00000
3.00000 1.00000
#24
Теория цифр
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Юный информатик стал исследовать, как изменяются суммы цифр натуральных чисел при умножении и делении на разные однозначные числа. Однажды он задался вопросом, можно ли восстановить число A, если нам известна сумма его цифр, а также сумма цифр числа D×A, где D — заданное однозначное число. Довольно быстро он установил, что для восстановления числа А этой информации недостаточно. Так, например, у чисел 9 и 45 одинаковые суммы цифр. Если же их умножить на 5, то получим числа 45 и 225, которые тоже имеют одинаковые суммы цифр.

Тогда юный информатик стал искать ответ на поставленный вопрос при условии, что нам известно K — количество десятичных знаков в числе A. К сожалению, и тут его ждало разочарование. У некоторых чисел, имеющих одинаковое количество цифр и одинаковые суммы цифр, после умножения на один и тот же множитель эти суммы опять оказываются одинаковыми. Такими числами, например, являются 42 и 51 при D = 3.

И тогда юный информатик поставил перед собой такую задачу: найти наименьшее K значное натуральное число A в десятичной системе счисления, которое имеет сумму цифр, равную S, а число D×A имеет сумму цифр, равную P.

Требуется написать программу, решающую поставленную задачу.

Входные данные

Вводятся четыре натуральных числа K, S, P, D (1 ≤ K ≤ 100, 1 ≤ S ≤ 9K, 1 ≤ P ≤ 9(K+1), 1 ≤ D ≤ 9).

Выходные данные

Выведите  число A, если оно существует, или –1, в противном случае. Число A не может начинаться с нуля.

Примечание

Решения, корректно работающие при K ≤ 40, будут оцениваться, исходя из 80 баллов.

Примеры
Входные данные
3 15 15 1
Выходные данные
159
Страница: 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест