Страница: 1 Отображать по:
#113545
Иллюзия сортировки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Известный программист пробует себя в роли иллюзиониста. Его коронный фокус состоит в следующем.

Для заданного массива из n целых неотрицательных чисел a1, a2, ..., an он быстро подбирает магическое число b. Целое неотрицательное число b называется магическим для массива, если применение операции побитового исключающего ИЛИ с этим числом к каждому элементу массива превращает его в отсортированный массив. Иначе говоря,

\(\) (a_1\oplus b) \le (a_2\oplus b) \le ... \le (a_n\oplus b) \(\)

где \(\oplus\) — операция побитового исключающего ИЛИ.

Чтобы фокус был более эффектным, после предъявления магического числа для заданного массива иллюзионист q раз выполняет следующее действие. Он предлагает зрителям изменить один из элементов массива и после этого снова пытается предъявить магическое число. При этом программист настолько отточил свое мастерство иллюзиониста, что каждый раз предъявляет зрителям минимальное возможное магическое число. Иногда фокус не удаётся, так как для полученного массива невозможно подобрать магическое число.

Требуется написать программу, которая по заданному исходно массиву, а также после каждого изменения элемента, вычисляет минимальное магическое число для полученного массива, либо определяет, что такого числа нет.

Примечание

Исключающее ИЛИ — это логическая операция, обозначаемая знаком \(\oplus\), которая задаётся следующей таблицей истинности:

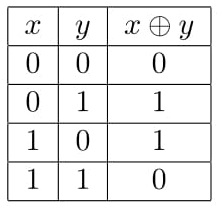
Определим побитовое исключающее ИЛИ для двух неотрицательных целых чисел x и y. Запишем каждое из целых чисел x и y в двоичной системе счисления, дополнив при необходимости более короткое из чисел ведущими нулями до равной длины. Побитовое исключающее ИЛИ двух целых чисел \(x\) и \(y\), обозначаемое также как \(\oplus\), это целое неотрицательное число, каждый разряд которого в двоичной системе счисления является исключающим ИЛИ соответствующих разрядов чисел \(x\) и \(y\). Например, \(5\oplus22=101_2\oplus10110_2=10011_2=19\).

Среди предложенных на олимпиаде языков программирования в языке Паскаль для обозначения исключающего ИЛИ используется оператор «xor», в остальных языках программирования используется оператор «^».

Входные данные

Первая строка входных данных содержит целое число n — количество чисел в массиве (1 ≤ n ≤ 106).

Вторая строка содержит n целых чисел a1, a2, ..., an — элементы массива (0 ≤ ai < 230).

Третья строка содержит целое число q — число изменений элемента массива (0 ≤ q ≤ 106).

Следующие q строк содержат по два целых числа pi и vi, где pi — номер элемента массива, который следует заменить (1 ≤ pi ≤ n), а vi — новое значение этого элемента (0 ≤ vi < 230).

Выходные данные

Выходные данные должны содержать (q + 1) целых чисел b0, b1, ..., bq, по одному в строке.

Значение b0 — либо минимальное возможное магическое число для исходного массива, либо  - 1, если такого числа не существует.

Для i от 1 до q значение bi — либо минимальное возможное магическое число для массива после первых i изменений, либо  - 1, если такого числа не существует.

Примеры
Входные данные
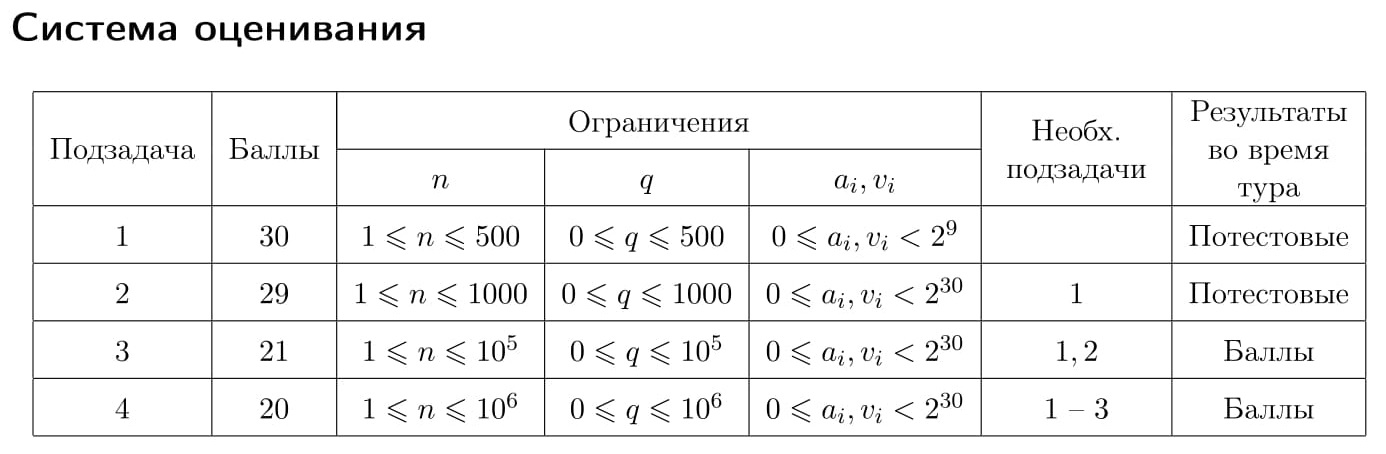
3
0 1 4
3
2 7
3 3
1 4
Выходные данные
0
2
-1
4
#113550
Антивещество
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

Компания тестирует технологию получения антивещества, используемого в качестве топлива в межпланетном звездолёте. Антивещество получается в результате специальных экспериментов в реакторе.

Известно n типов экспериментов, приводящих к получению антивещества. В результате проведения эксперимента i-го типа в выходной контейнер реактора добавляется от li до ri граммов антивещества. Из соображений безопасности запрещается накапливать в контейнере более a граммов антивещества.

Затраты на проведение эксперимента i-го типа составляют ci, а стоимость одного грамма полученного антивещества составляет 109.

Если после проведения экспериментов в контейнере образовалось t граммов антивещества, а суммарные затраты на проведение экспериментов в реакторе составили s, то прибыль определяется по формуле (t·109 - s). Компании необходимо разработать стратегию проведения экспериментов, позволяющую максимизировать прибыль, которую можно гарантированно получить.

В зависимости от результатов предыдущих экспериментов стратегия определяет, эксперимент какого типа следует провести, или решает прекратить дальнейшее выполнение экспериментов. Стратегия позволяет гарантированно получить прибыль x, если при любых результатах проведения экспериментов: во-первых, в контейнере реактора оказывается не более a граммов антивещества, во-вторых, прибыль составит не менее x.

Например, пусть возможен только один тип эксперимента, порождающий от 4 до 6 граммов антивещества, затраты на его проведение равны 10, а вместимость контейнера составляет 17 граммов. Тогда после двукратного проведения эксперимента в контейнере может оказаться от 8 до 12 граммов антивещества. Если получилось 12 граммов, то больше проводить эксперимент нельзя, так как в случае получения 6 граммов антивещества контейнер может переполниться. В остальных случаях можно провести эксперимент в третий раз и получить от 12 до 17 граммов антивещества. В худшем случае придётся провести эксперимент трижды, затратив в сумме 30, прибыль составит (12·109 - 30) = 11 999 999 970.

Требуется написать программу, которая определяет максимальную прибыль x, которую гарантированно можно получить.

Входные данные

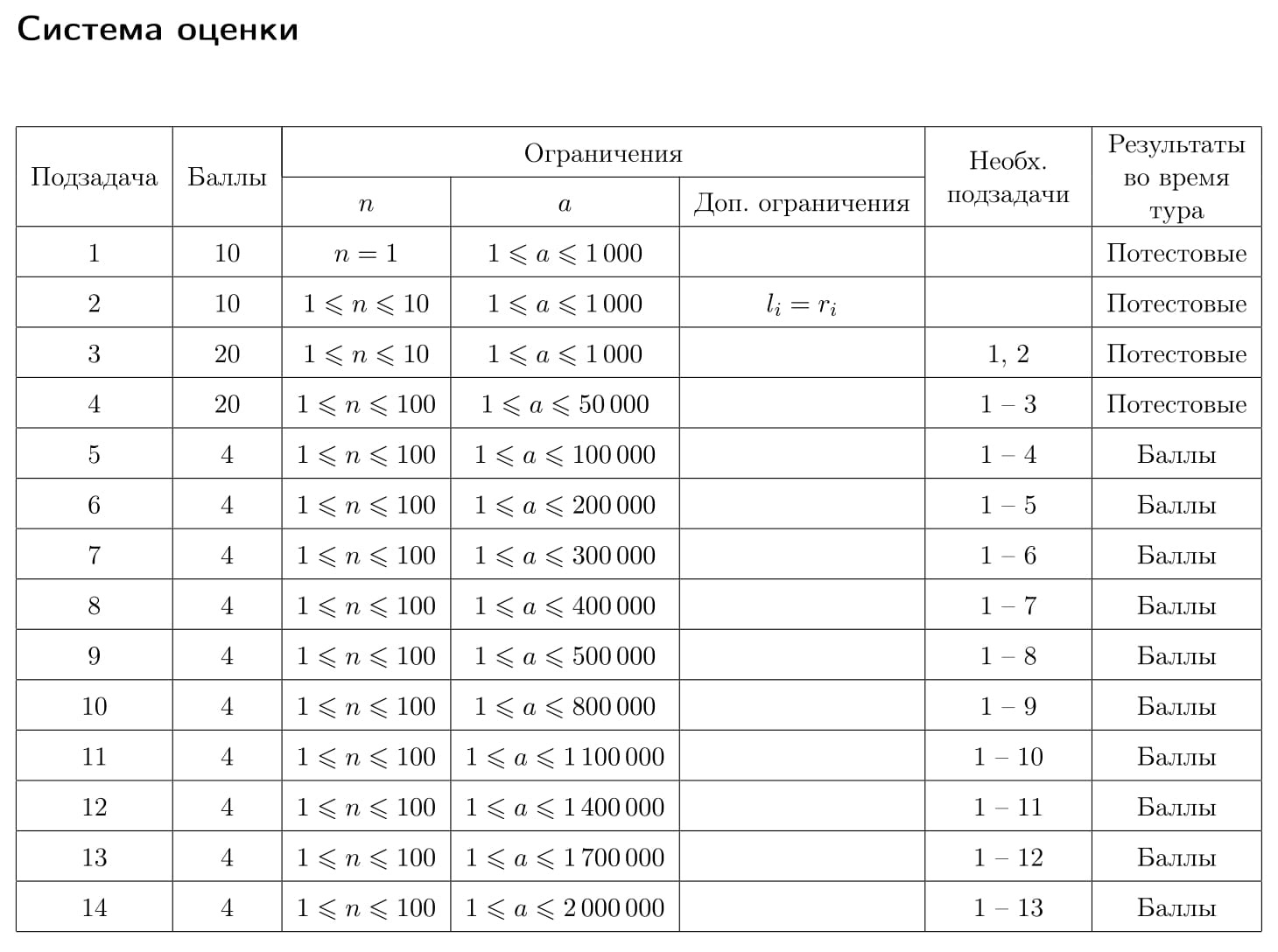
Первая строка входных данных содержит два целых числа: n — количество типов экспериментов и a — максимально допустимое количество антивещества в контейнере (1 ≤ n ≤ 100, 1 ≤ a ≤ 2 000 000).

Следующие n строк содержат по три целых числа li, ri и ci — минимальное и максимальное количество антивещества, получаемое в результате эксперимента типа i, и затраты на эксперимент этого типа, соответственно (1 ≤ li ≤ ri ≤ a, 1 ≤ ci ≤ 100).

Выходные данные

Выходные данные должны содержать одно целое число — максимальную прибыль x, которую гарантированно можно получить.

Примеры
Входные данные
1 17
4 6 10
Выходные данные
11999999970
Входные данные
2 11
2 2 100
3 5 5
Выходные данные
9999999890
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест