В местном книжном магазине акция: "Возьми 3, заплати за 2 самых дорогих". То есть, каждый покупатель, который возьмет 3 книги, получит самую дешевую из них бесплатно. Разумеется, он может взять и больше книг, и, некоторым образом разделив их на группы по 3, получать самую дешевую в каждой группе бесплатно. Например, пусть цены книг, выбранных покупателем, будут следующие: 10 3 2 4 6 4 9. Он может разделить их на группы таким образом: (10, 3, 2), (4, 6, 4), (9). Тогда он получит книгу стоимостью 2 из первой группы и книгу стоимостью 4 из второй группы бесплатно. При этом из третьей группы он ничего не получит бесплатно, так как в ней всего 1 книга. Девушка, работающая в магазине, очень добрая и всегда хочет помочь покупателю заплатить как можно меньше денег за выбранные книги. Помогите ей для выбранных покупателем книг распределить их по группам так, чтобы сумма денег, в результате заплаченная покупателем, была минимальна.
В первой строке записано одно натуральное число N ( 1 ≤ N ≤ 100000 ) - количество книг, выбранных покупателем. В каждой из следующих N строк записано одно натуральное число C i ( 1 ≤ C i ≤ 100000 ) - цена соответствующей книги.
В единственной строке выведите одно целое число - минимальную цену, которую может заплатить покупатель за выбранные книги.
4 3 2 3 2
8
6 6 4 5 5 5 5
21
Любимый всем кукольник Гепетто открыл новую пиццерию. Он хочет делать самую лучшую пиццу в городе, но не хочет иметь маленький ассортимент пицц.
Гепетто делает свои пиццы из N ингредиентов, пронумерованных от 1 до N . Всё было бы хорошо, но к сожалению он не может класть некоторые ингредиенты в одну пиццу.
Всего есть M пар ингредиентов, которые нельзя класть в одну пиццу. Помогите Гепетто узнать, сколько различных пицц он может cделать.
Первая строка содержит два целых числа N и M ( 1 ≤ N ≤ 20 , 0 ≤ M ≤ 400 ). Следующие M строк содержат по два различных чсла a и b , обозначающие, что класть ингредиенты a и b запрещено класть в одну пиццу ( 1 ≤ a , b ≤ N ).
Выведите одно число – ответ на задачу
В первом примере Гепетто может сделать пиццы из наборов {}, {1}, {2}, {3}, {1, 3}. Во втором примере он может использовать любую комбинацию ингредиентов. В третьем примере он может сделать пиццы из наборов {}, {1}, {2}, {3}.
3 2 1 2 2 3
5
3 0
8
3 3 1 2 1 3 2 3
4
Вы наверняка слышали легенду о Короле Артуре и Рыцарях Круглого Стола. Практически все версии этой истории указывают на то, что круглость Круглого Стола тесно связана с верой Артура в равенство среди рыцарей. Это ложь! На самом деле выбор Артура касательно формы стола вызван его детской травмой.
В реальности Артур был принужден убирать и мыть квадратные столы с юного возраста после того как на них играли в бирюльки. После соревнований по этой игре обычно на столе остается множество палочек, не касающихся друг друга. В духе соревнования, организаторы установили свод строгих правил для уборщиков. Точнее, палочки со стола должны быть убраны одна за другой путем их сдвига к ближайшему к уборщику краю стола. Они не должны вращаться и касаться других палочек в процессе перемещения.
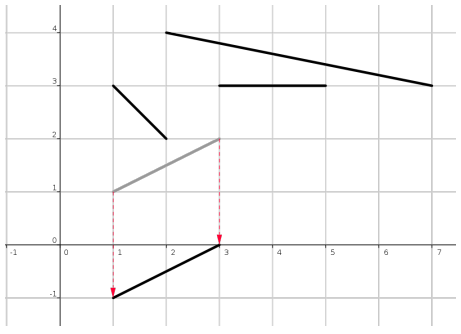
В этой задаче представим стол на координатной плоскости как квадрат с противоположными вершинами в точках (0, 0) и (10000, 10000), где палочкам соответствуют прямые отрезки, лежащие внутри квадрата. Предположим, что Артур сидит у края стола, прилежащего к оси X. Тогда уборка палочек со стола сводится к передвижению их к оси X, покуда они не упадут со стола. Ваша задача - определить порядок уборки палочек со стола, который соответствует условиям из предыдущего абзаца.
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 5000 ) - количество палочек на столе. Каждая из следующих N строк содержит 4 целых числа x 1 , y 1 , x 2 , y 2 ( 0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 10000 ), обозначающих крайние точки палочек.
В единственной строке выведите N целых чисел - номера палочек в том порядке, в котором они должны быть убраны со стола. Если существует несколько решений, выведите любое из них.
4 1 3 2 2 1 1 3 2 2 4 7 3 3 3 5 3
2 4 1 3
4 0 0 1 1 1 2 0 3 2 2 3 3 4 0 3 1
4 3 1 2
3 4 6 5 5 2 1 15 1 3 2 8 7
2 3 1
Известно, что в солнечной системе есть 8 планет и один планетоид. Мало кто знает, что ещё есть секретная планета, населенная медведями. Именно туда ассоциация Savez отправляет бравого генерала Хенрика для изучения медведей. Выяснилось, что медведи умеют телепортироваться. Расчётливый генерал Хедрик решил завербовать их в свою армию.
У одного медведя есть N строк (обозначим i -ю из них x i ). Исследования показывают, что количество раз, которое может телепортироваться медведь равно длине наибольшей подпоследовательности этих строк, удовлетворяющей такому правилу: строки x i и x j ( i < j ) могут принадлежать одной такой последовательности, если x i является и префиксом, и суффиксом x j .
Помогите уставшему от долгого полёта генералу Хендрику определить, сколько телепортаций сможет сделать данный медведь.
В первой строке содержится одно целое число N – количество строк, которые есть у медведя. В последующих N строках содержатся сами эти строки. Входной файл содержит не более двух миллионов символов.
Выведите одно число – ответ на вопрос любопытного генерала Хендрика.
В первом примере наибольшая последовательность A -> AA -> AAA В третьем примере наибольшая последовательность A -> A -> A или B -> B -> B
5 A B AA BBB AAA
3
5 A ABA BBB ABABA AAAAAB
3
6 A B A B A B
3
Юный Мирко решил купить куклу вуду. Учитывая что он крайне заинтересован в том, ктобы купить ее как можно дешевле, он начал отслеживать цены на кукол вуду каждый день. Его список состоит из цен на куклы в последние N дней, где a i обозначает цену куклы i дней назад.
Мирко думает, что нашел связь между средней ценой кукол в течении нескольких последовательных дней и ценой куклы в следующий день. Он хочет проверить свою догадку и задался вопросом: "Для данного числа P , сколько существует наборов последовательных дней в течении последних N дней, для которых средняя цена куклы в эти дни составляет не менее P ".
Два набора последовательных дней считаются различными, если у них отличается первый или последний день.
Первая строка содержит одно целое число N ( 1 ≤ N ≤ \(10^6\) ), количество дней в списке Мирко. Вторая строка содержит N целых чисел a i ( 0 ≤ a i ≤\(10^9\) ) - цены кукол в соответствующие дни. Третья строка содержит одно целое число P ( 0 ≤ P ≤\(10^9\) ).
Выведите одно целое число - ответ на вопрос Мирко для данного P .
3 1 2 3 3
1
3 1 3 2 2
5
3 1 3 2 3
1