#111410

Результаты гонки

Темы: [Разбор случаев]

Формула TheByte это самое известное гоночное соревнование в Байтландии. Соревнование уже завершено и каждый из n гонщиков заработал какое-то целое неотрицательное количество очков. Гонщик, у которого больше очков, займет более высокое место.

Окончательные результаты еще не объявлены, но уже известно, что сумма все зарабонных гонщиками очков равна p, и среди лучших k гонщиков есть только d различных результатов.

Байтланд Таймс просит вас угадать окончательные результаты, основываясь на данной информации.

Входные данные

Единственная строка входного файла содержит четыре целых числа: n — количество гонщиков, p — суммарное количество очков, k и d — количество различных результатов среди k лучших гонщиков (1 ≤ k ≤ n ≤ 1000; 0 ≤ p ≤ 1 000 000; 1 ≤ d ≤ k).

Выходные данные

Выведите возможные результаты, которые соответствуют данным n, p, k и d.

Если возможно создать корректные результаты, вы должны вывести n строк, i-тая из которых будет содержать количество очков, заработанных i-тым гонщиком. Гонщики должны быть упорядочены по убыванию количества очков.

Если не существует возможных результатов, удовлетворяющих данной информации, выведите одну строку "Wrong information".

Примеры тестов

Входные данные

3 4 2 2

Выходные данные

2
1
1

Входные данные

3 5 2 2

Выходные данные

3
2
0

Входные данные

2 5 2 1

Выходные данные

Wrong information

Решения, работающие в случае, если P не превосходит 2000, будут набирать не менее 30 баллов.

#111411

Сетка

Темы: [Конструктив] [Разбор случаев] [Элементарная геометрия]

Геральд потратил несколько часов, рисуя прямоугольную сетку на листе бумаги. Сначала он нарисовал несколько вертикальных линий на одинаковом расстоянии d_x между ними. После этого он нарисовал несколько горизонтальных линий. Они также находились на одинаковом расстоянии d_y друг от друга.

Пока Геральд отдыхал от трудов, его брат Майк пришел и нарисовал прямую линию на листе бумаги. Геральд разозлился и приказал Майку стереть все лишнее с бумаги.

$\text{[math]}$

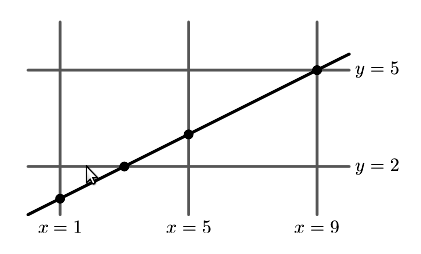
Но Майк не воспринял всерьез слова брата и стер все. Но он заметил, что точки пересечения его линии с сеткой были достаточно жирными для того, чтобы быть заметными даже после стирания.

Помогите Геральду восстановить параметры исходной сетки.

Входные данные

Первая строка входного файла содержит одно целое число n — количество точек пересечения (3 ≤ n ≤ 100 000).

Каждая из следующих n строк содержит два целых числа x_i, y_i — координаты одной из точек пересечения. Координаты не превосходят 10⁹ по абсолютной величине.

Все точки пересечения различны. Других общих точек, кроме описанных выше, у сетки и прямой Майка нет.

Выходные данные

Выведите шесть целых чисел x₁, x₂, d_x, y₁, y₂ и d_y. Первые три числа описывают набор вертикальных прямых: минимальная x-координата вертикальной прямой, максимальная x-координата вертикальной прямой и расстояние между соседними вертикальными линиями ( - 10⁹ ≤ x₁ ≤ x₂ ≤ 10⁹; 0 < d_x ≤ 2·10⁹). Следующие три числа аналогично описывают набор горизонтальных линий ( - 10⁹ ≤ y₁ ≤ y₂ ≤ 10⁹; 0 < d_y ≤ 2·10⁹).

Гарантируется, что хотя бы одно решение существует.

Примеры тестов

Входные данные

Выходные данные

1 9 4 2 5 3

#113805

Тетрис

Темы: [Применение обхода в глубину] [Разбор случаев]

Ивица — страстный компьютерщик. Недавно он начал работать над своей первой компьютерной игрой — клоном популярного тетриса. Хотя игра далека от завершения, его программа уже поддерживает размещение в матрице N × M пяти разных фигур Тетриса (показанных на изображении ниже) в матрице. Перед тем, как поместить фигуру в матрицу, её можно поворачивать на 90 градусов произвольное число раз и можно окрашивать. Кроме того, текущая версия игры не поддерживает размещение фигуры, если она при этом выходит за границы матрицы или перекрывается с другими существующими фигурами в матрице.

$\text{[math]}$

Пока Ивица учился в школе, его сестра Марика начала игру и случайным образом повернула, покрасила и поместила фигуры, но таким образом, что соседние фигуры окрашены по-разному. Две фигуры смежны, если они имеют общую сторону или общий угол.

Он хочет знать для каждого из пяти типов фигуры, сколько таких фигур его сестра разместила в матрицу, пока он занят улучшением игры.

Входные данные

Первая строка ввода содержит положительные целые числа N и M ( 1 ≤ N , M ≤ 10 ), которые представляют количество строк и столбцов матрицы Тетриса. Каждая из следующих N строк содержит M символов, которые представляют матрицу. Каждый символ может быть « . », что означает пустую клетку или строчной буквой английского алфавита, которая представляет часть фигуры. Различные буквы представляют разные цвета, а клетки одной фигуры имеют одинаковый цвет.

Гарантируется, что вводная матрица могла быть получена последовательным добавлением фигур Тетриса в изначально пустую матрицу.

Выходные данные

Вы должны вывести ровно пять строк. i -я строка должна содержать количество фигур i -го типа, находящихся в данной матрице.

Система оценки

$\text{[math]}$

Примеры

Входные данные

4 5
aaaa.
.bb..
.bbxx
...xx

Выходные данные

Входные данные

4 5
.aab.
aabb.
.cbaa
cccaa

Выходные данные

Входные данные

5 7
.c.....
ccdddd.
caabbcc
aabbacc
...aaa.

Выходные данные

#113810

Покос

Темы: [Формула] [Разбор случаев]

Мирко нужно купить землю, чтобы построить дом для своей семьи. Он присмотрел K участков. Для простоты будем считать, что участок представляет собой поле с N строками и M столбцами, N × M клеток в сумме.

Мирко знал, что до начала строительства участок надо поддерживать в порядке. По этой причине он приобрёл газонокосилку. Для покоса участка ему нужно проехать по каждой клетке поля хотя бы раз. Он может начать с любой клетки, смотря в одно из четырёх основных направлений (вверх, вниз, влево или вправо). Его газонокосилка может двигаться только вперёд (перемещаться в следующую клетку вдоль текущего направления) или поворачиваться на 90 градусов. К тому же, ради безопасности, Мирко может косить только на своём участке, не выходя за пределы поля.

Так как поворачивать газонокосилку непросто, Мирко хочет минимизировать количество поворотов газонокосилки. Для каждого из K участков земли ему нужно знать минимальное число поворотов для покоса. Помогите Мирко с этой задачей.

Входные данные

В первой строке вводится натуральное число K ( 1 ≤ K ≤ 50 000 ) — число запросов. В каждой из следующих K строк вводятся два натуральных числа N и M ( 1 ≤ N , M ≤ 10 ⁶ ) — размеры поля для каждого запроса.

Выходные данные

Для каждого запроса в отдельной стоке выведите минимальное число поворотов газонокосилки, которое потребуется для покоса участка.

Система оценки

Программы, верно работающие на тестах, в которых K = 1 , 1 ≤ N , M ≤ 500 , оцениваются в 50 баллов.

Примечание

В первом примере первый участок можно покосить без поворотов, если Мирко встанет в первой клетке поля и пойдёт вперёд. Аналогичная идея относится и ко второму участку.

Примеры

Входные данные

2
1 10
10 1

Выходные данные

0
0

Входные данные

Выходные данные

0
4
4

Входные данные

2
5 8
6 4

Выходные данные

8
6

#113938

Уравнения математической магии

Темы: [Битовые операции] [Разбор случаев]

Колоссально! — воскликнул горбоносый. — Программист! Нам нужен именно программист.

Аркадий и Борис Стругацкие, Понедельник начинается в субботу

Изучая книгу «Уравнения математической магии» Роман Ойра-Ойра и Кристобаль Хунта обнаружили интересное уравнение: $a - (a \oplus x) - x = 0$ для заданого $a$, где знаком $\oplus$ обозначено побитовое исключающее ИЛИ (XOR) двух чисел (эта операция обозначается как ^ или xor во многих современных языках программирования). Ойра-Ойра быстро нашел $x$, являющееся решением, однако Кристобалю Хунте результат Ойры-Ойры показался недостаточно интересным, поэтому он спросил коллегу, сколько существует неотрицательных решений данного уравнения. Такая задача оказалась для Ойры-Ойры слишком сложной, поэтому он обратился за помощью к Вам.

Входные данные

Вам предстоит решить задачу для нескольких возможных значений параметра $a$. В первой строке находится целое число $t$ ($1 \le t \le 1000$) — количество этих значений.

В последующих $t$ строках находятся значения параметра $a$, каждое значение — целое число от $0$ до $2^{30} - 1$ включительно.

Выходные данные

Для каждого значения параметра $a$ выведите строке одно целое число — количество неотрицательных решений уравнения с данным значением параметра. Ответы выводите в том же порядке, в каком параметры следуют во входных данных.

Можно доказать, что количество решений всегда конечно.

Примечание

Определим операцию побитового исключительного ИЛИ (XOR).

Пусть даны два целых неотрицательных числа $x$ и $y$, рассмотрим их двоичные записи (возможно с ведущими нулями): $x_k \dots x_2 x_1 x_0$ и $y_k \dots y_2 y_1 y_0$. Здесь $x_i$ это $i$-й бит числа $x$, а $y_i$ это $i$-й бит числа $y$.

Пусть $r = x \oplus y$ — результат операции XOR над числами $x$ и $y$. Тогда двоичной записью $r$ будет $r_k \dots r_2 r_1 r_0$, где:

 r_i = \left\{ \begin{aligned} 1, ~ \text{если} ~ x_i \ne y_i \\ 0, ~ \text{если} ~ x_i = y_i \end{aligned} \right. 

Для первого значения параметра только $x = 0$ является решением уравнения.

Для второго значения параметра решениями уравнения являются $x = 0$ и $x = 2$.

Примеры

Входные данные

Выходные данные

1
2
1073741824