--->
21 задач
<---
Источники
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Представьте себе бесконечную клетчатую бумагу. Изначально все клетки белые, но некоторые из них можно закрасить черным.
Назовем две клетки 8-связными, если у них есть общая сторона или точка. 8-путем назовем последовательность клеток от A до B, так что все клетки в последовательности черные, и две соседние клетки в последовательности являются 8-связными. Набор черных клеток назовем рисунком, если существует 8-путь из каждой клетки набора в любую другую клетку этого набора.
Назовем две клетки 4-связными, если у них есть общая сторона. 4-путем назовем последовательность клеток от A до B, так что все клетки в последовательности белые, и две соседние клетки в последовательности являются 4-связными. Конечный набор белых клеток назовем пустотой, если существует 4-путь из каждой клетки набора в любую другую клетку этого набора и к нему невозможно добавить ни одной белой клетки так, чтобы предыдущее условие не нарушилось.
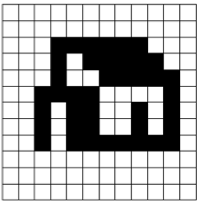
Будем говорить, что рисунок имеет высоту H и ширину W если он охватывается прямоугольником с высотой H и шириной W и не охватывается никаким прямоугольником меньшего размера. На иллюстрации показан рисунок с высотой 7 и шириной 9. По заданным числа H, W и N постройте рисунок высоты H, ширины W содержащий ровно N пустот.
Входные данные
Входной файл содержит несколько тестовых блоков. Первая строка содержит число T (1 ≤ T ≤ 100) – количество тестовых блоков.
Каждая из следующих T строк описывает один тестовый блок. Описание состоит из целых чисел H, W и N (1 ≤ H, W ≤ 20, 1 ≤ N ≤ 200).
Выходные данные
Выходной файл должен содержать следующую информацию для каждого тестового блока:
Если рисунок можно построить, то выведите любую допустимую фигуру, удовлетворяющую условию задачи, состоящую из H строк по W символов в каждой. Выводите символ “.” для обозначения черной клетки и символ “#” для обозначения белой клетки.
Если рисунок построить нельзя, выведите одну строку, содержащую слово “Impossible”.
Вывод данных для разных тестовых блоков разделяйте одной пустой строкой.
Примеры тестов
Входные данные
3 7 9 2 20 20 22 5 5 10
Выходные данные
#......## #.#.....# #.##..... ....####. .#..##.#. .#..##.#. .#....... .#####.######.#####. ..###...####...###.. ...#.....##.....#... .................... ....##..##..#...#... ...#.#.#..#.##.##... ...###.#....#.#.#... ...#.#.#..#.#...#... ...#.#..##..#...#... .................... .................... .###..##..###...##.. ..#..#..#.#..#.#..#. ..#..#....###..#.... ..#..#..#.#....#..#. .###..##..#.....##.. .................... ...#.....##.....#... ..###...####...###.. .#####.######.#####. Impossible
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Вы занимаетесь компьютерной безопасностью. Недавно один из ваших клиентов разработал новый тест, предназначенных для того, чтобы отличить человека от программы. Ваша задача — протестировать его эффективность.
Тест основан на игре «Морской бой». Эта игра проводится на клетчатом поле размером 10 × 10 клеток. Перед началом игры вы должны разместить десять кораблей на этом поле. Каждый корабль задается числом последовательных клеток, расположенных горизонтально или вертикально. Вы должны разместить один четырехклеточный корабль, два трехклеточных, три двухклеточных и четыре одноклеточных корабля. Никакие два корабля не могут иметь общую или соседние по стороне или углу клетки.
После того, как все корабли расставлены, тест продолжается в течение некоторого количества раундов. В каждом раунде выбирается одна клетка, по которой производится стрельба. Корабль тонет, если по каждой его клетке пришлось не менее одного попадания. Тест заканчивается, когда все корабли утонули.
Назовем сложностью расположения кораблей количество раундов, которое потребуется для того, чтобы завершить тест. Идея теста в том, что люди будут создавать более сложные расположения, чем программы.
Вы же выяснили, что порядок, в котором производится стрельба по клеткам, заранее задан, по каждой клетке стреляют ровно один раз. Теперь вам нужно написать программу, которая создает самое сложное расположение кораблей.
Входные данные
Входной файл состоит из десяти строк, каждая из которых содержит десять чисел. Каждое число обозначает номер раунда, в котором по соответствующей клетке будет вестись стрельба. Все числа различны и лежат в диапазоне 1... 100.
Выходные данные
Выведите какое-нибудь оптимальное расположение кораблей для данного порядка стрельбы. Пустые клетки должны быть обозначены точкой ('.'), занятые клетки должны быть обозначены решёткой ('#').
Примеры тестов
Входные данные
1 2 3 4 5 6 7 8 9 10
36 37 38 39 40 41 42 43 44 11
35 64 65 66 67 68 69 70 45 12
34 63 84 85 86 87 88 71 46 13
33 62 83 96 97 98 89 72 47 14
32 61 82 95 100 99 90 73 48 15
31 60 81 94 93 92 91 74 49 16
30 59 80 79 78 77 76 75 50 17
29 58 57 56 55 54 53 52 51 18
28 27 26 25 24 23 22 21 20 19
Выходные данные
...####...
..........
#....##...
#.#.....#.
........#.
...###....
.#........
........#.
..#.....#.
.....#..#.
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Геральд потратил несколько часов, рисуя прямоугольную сетку на листе бумаги. Сначала он нарисовал несколько вертикальных линий на одинаковом расстоянии dx между ними. После этого он нарисовал несколько горизонтальных линий. Они также находились на одинаковом расстоянии dy друг от друга.
Пока Геральд отдыхал от трудов, его брат Майк пришел и нарисовал прямую линию на листе бумаги. Геральд разозлился и приказал Майку стереть все лишнее с бумаги.
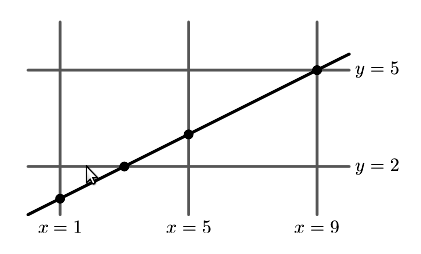
Но Майк не воспринял всерьез слова брата и стер все. Но он заметил, что точки пересечения его линии с сеткой были достаточно жирными для того, чтобы быть заметными даже после стирания.
Помогите Геральду восстановить параметры исходной сетки.
Входные данные
Первая строка входного файла содержит одно целое число n — количество точек пересечения (3 ≤ n ≤ 100 000).
Каждая из следующих n строк содержит два целых числа xi, yi — координаты одной из точек пересечения. Координаты не превосходят 109 по абсолютной величине.
Все точки пересечения различны. Других общих точек, кроме описанных выше, у сетки и прямой Майка нет.
Выходные данные
Выведите шесть целых чисел x1, x2, dx, y1, y2 и dy. Первые три числа описывают набор вертикальных прямых: минимальная x-координата вертикальной прямой, максимальная x-координата вертикальной прямой и расстояние между соседними вертикальными линиями ( - 109 ≤ x1 ≤ x2 ≤ 109; 0 < dx ≤ 2·109). Следующие три числа аналогично описывают набор горизонтальных линий ( - 109 ≤ y1 ≤ y2 ≤ 109; 0 < dy ≤ 2·109).
Гарантируется, что хотя бы одно решение существует.
Примеры тестов
Входные данные
4
1 1
5 3
3 2
9 5
Выходные данные
1 9 4 2 5 3
#112032
Темы:
[Алгоритмы сортировки]
[Конструктив]
Источники:
[
Личные олимпиады,
Открытая олимпиада школьников,
2012-2013,
Заключительный этап - второй тур,
Задача A
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Каждое утро капитан Ъ проводит занятия по строевой подготовке в возглавляемой им роте солдат. Всего в роте N солдат, каждый из которых носит форму определенного цвета. Различных цветов формы не более 26, так что для удобства солдаты обозначают цвета строчными латинскими буквами. Таким образом, каждому из \(N\) солдат соответствует буква от 'a' до 'z' — цвет его формы.
За многие месяцы службы солдаты выяснили, что капитан пребывает в наилучшем расположении духа в том случае, когда цвета формы солдат в шеренге образуют определенную последовательность. Недолго думая, они выписали соответствующую строку \(S\) из \(N\) букв на асфальте и договорились, что отныне каждый должен при построении вставать именно на ту букву, которая соответствует цвету его формы.
Но к 23 февраля солдаты решили удивить капитана и поменяться местами так, чтобы \(каждый\) солдат встал не на ту букву, которая соответствует цвету его формы. Так, солдат с цветом формы 'q' может встать на любую букву, кроме буквы 'q', иначе удивление капитана будет недостаточным.
Помогите солдатам организовать праздничное построение: по данной строке \(S\), обозначающей старую последовательность цветов, выведите строку \(T\), являющуюся перестановкой символов строки \(S\) и обозначающую новую последовательность цветов. i-й символ строки T должен отличаться от i-го символа строки \(S\).
Входные данные
В первой строке входного файла содержится единственное целое число \(N\) — количество солдат в роте \((1 \le N \le 100 000)\). Во второй строке содержится строка S, состоящая из \(N\) строчных латинских букв.
Выходные данные
Единственная строка выходного файла должна содержать искомую строку \(T\), если задумка солдат осуществима, и «Impossible» в противном случае. Если верных ответов несколько, выведите любой из них.
Система оценки
Тесты к этой задаче состоят из четырех групп. Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы.
0. Тесты 1—2. Тесты из условия, оцениваются в ноль баллов.
1. Тесты 3—21. В тестах этой группы \(N \le 9\). Эта группа оценивается в 30 баллов.
2. Тесты 22—36. В тестах этой группы \(N \le 200\), а строка не может содержать никаких букв, кроме 'a', 'b' и 'c'. Эта группа оценивается в 30 баллов независимо от первой.
3. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов.
Примеры
Входные данные
9 olimpiada
Выходные данные
iapdialom
Входные данные
7 baaaaaa
Выходные данные
Impossible
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Ассоциация Великих Машин (АВМ) в последнее время совершила прорыв в археологических раскопках. Они нашли древний артефакт расписанный кодами , безусловно, созданный какой-то великой машиной много лет назад развитой ныне исчезнувшей цивилизацией. Исследователи предполагают, что эти коды скрывают знания этой цивилизации. Однако, прогресс в расшифровке кода остановился, потому что некоторые слова были сильно повреждены, а некоторые слова были непригодны для чтения.
Исследователи выяснили, что Великая Машина использовала слова только определённой структуры. Каждое слово состоит из цифр от 0 до 7 (включительно) и построено из слова "s" одним или несколькими из следующих правил:
s → 0
s → 1s
s → 2ss
s → 3sss
s → 4ssss
s → 5sssss
s → 6ssssss
s → 7sssssss
Каждое из этих правил может быть применено несколько раз, если это необходимо, и они могут быть использованы в любом порядке. Использование правила заменяет одно выбранное "s" на правую часть определённого превращения. Например, слово "2s0" может трансформироваться в "22ss0" по третьему правилу. Пожалуйста, помогите исследователям реконструировать эти слова и расшифровать все сообщения древней цивилизации. Вам предоставлен остаток правильного слова только из цифр от 0 до 7. Исследователи уверенны, что небольшая часть букв была утеряна, поэтому они хотят определить правильное слово минимальной длины, которое будет содержать данное слово как подпоследовательность.
Входные данные
Входной файл содержит одну непустую строку, состоящей из цифр от 0 до 7. Общее количество цифр будет меньше или равно 30 000.
Выходные данные
Вывести слово минимальной длины которое содержит в себе как подпоследовательность вводимые слово. В случае существования нескольких строк минимальной длины вывести любую.
Примеры
Входные данные
00
Выходные данные
200
Входные данные
22
Выходные данные
22000
Входные данные
3002010
Выходные данные
3002010
Выбрано
:
|