Вася записывает в клетки квадратной таблицы NxN натуральные числа по порядку, сначала заполняя первую строку слева направо, затем вторую и т.д. (см. рисунок слева). Петя заполняет такую же таблицу, расставляя числа сначала в первый столбец сверху вниз, затем во второй столбец и т.д.
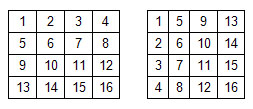
При этом оказалось, что некоторые числа и Вася, и Петя записали в одну и ту же клетку (например, число 6 записано во вторую строку второго столбца обеих таблиц).
Вам требуется написать программу, выводящую все числа, которые в обеих таблицах записаны в одних и тех же клетках.
Вводится одно число - размер таблицы.
Программа должна вывести все числа, которые в обеих таблицах стоят на одном и том же месте, в порядке возрастания, через пробел.
Размер таблицы - натуральное число, не превосходящее 100.
4
1 6 11 16
1
1
Многие натуральные числа можно представить в виде N = 3A + 5B, где A и B - целые неотрицательные числа. Например, 11=3x2+5x1, 20=3x0+5x4.
Вам требуется по заданному числу определить, можно ли его представить в таком виде, и если это возможно, найти подходящие A и B.
Вводится одно число.
Программа должна вывести два целых неотрицательных числа A и B, разделенных пробелом, если такие числа существуют. В противном случае выведите слово IMPOSSIBLE. Если решений несколько, выведите любое из них.
Программа должна верно работать для натуральных чисел, не превосходящих 10 000.
23
1 4
4
IMPOSSIBLE
Дан набор из N отрезков различной длины. Сколькими способами можно выбрать из этих отрезков три, из которых можно составить (невырожденный) треугольник?
Сначала вводится количество отрезков, затем длины этих отрезков (еще N чисел).
Программа должна вывести одно число - искомое количество способов.
Количество отрезков - не менее 3 и не более 20. Длина каждого отрезка - натуральное число, не превосходящее 1000. Все отрезки имеют разную длину.
4 1 3 2 4
1
3 10 100 1000
0
На доске стоит белая шашка. Требуется определить, может ли она попасть в заданную клетку, делая ходы по правилам (не превращаясь в дамку).
Вводится клетка, где стоит шашка, в шахматной нотации, а затем, через пробел, клетка, куда шашка должна попасть.
Выведите слово YES (заглавными буквами), если шашка может попасть из начальной клетки в указанную, и NO в противном случае.
Доска имеет размер 8x8, вертикали нумеруются маленькими латинскими буквами от a до h, горизонтали - числами от 1 до 8. Исходная и конечная клетки не совпадают.
a1 b2
YES
b2 a1
NO
a1 h7
NO
Напишите рекурсивную функцию, возводящую число a в степень n. Гарантируется, что все числа "помещаются" в стандартные вещественные (a и ответ) и целые (n) типы.
Вводится 2 числа - a и n (число n может быть отрицательным).
Необходимо вывести значение an
2 -1
0.5