Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Вася и Петя играют в увлекательную игру. Вася выписал подряд числа от 1 до N. А Петя выписал P пар чисел (Ai, Bi).
Теперь Вася преобразует имеющуюся последовательность чисел - он меняет местами числа в этой последовательности. Если некоторая пара чисел (Ai, Bi) выписана Петей, то Вася имеет право в любой момент взять числа из последовательности, стоящие на местах Ai и Bi и поменять их местами.
Например, если N=5. Тогда изначально Васей выписана последовательность
1 2 3 4 5
Пусть Петя написал две пары чисел: (1,2) и (2,5). Тогда Вася в любой момент может менять числа, стоящие на 1 и 2 местах, или же числа, стоящие на 2 и 5 местах.
Например, он может последовательно получить следующие последовательности:
2 1 3 4 5 (поменяв числа на 1 и 2 местах)
2 5 3 4 1 (поменяв числа на 2 и 5 местах)
5 2 3 4 1 (поменяв числа на 1 и 2 местах).
Пете не показываются промежуточные последовательности, а выписывается лишь полученная на последнем шаге.
От Пети требуется проверить, мог ли Вася получить такую последовательность не нарушая правил игры, и если мог, то указать, в результате какой последовательности обменов (при этом не требуется, чтобы число обменов было минимально возможным).
Напишите программу, которая поможет Пете справиться с этой задачей.
Сначала записано число N (1≤N≤100) – количество чисел в последовательности. Дальше идет N чисел – последовательность, полученная Васей (в последовательности каждое из чисел от 1 до N встречается ровно один раз).
Далее идет число P (0≤P≤10000) – количество пар чисел, выписанных Петей. Далее записано P пар чисел (каждое число пары – из диапазона от 1 до N).
В первую строку выходного файла выведите сообщение YES (если такая последовательность могла быть честно получена Васей) и NO (если такую последовательность Вася не мог получить, не нарушая правил игры).
В случае, если такая последовательность могла быть получена, далее выведите способ ее получения (если вариантов несколько, выведите любой из них). Сначала выведите число K – количество операций обмена (оно не должно превышать 100000), а затем K пар чисел, задающих номера мест, на которых стоят обмениваемые элементы (числа в паре могут быть выданы в любом порядке). Гарантируется, что если решение существует, то существует решение с числом обменов, не превышающим 100000.
5 5 2 3 4 1 2 1 2 2 5
YES 3 1 2 2 5 1 2
5 2 3 4 5 1 2 1 2 2 5
NO
SMS-сообщения на мобильном телефоне марки MOBILO набираются только заглавными английскими буквами. Для набора буквы нужно нажать кнопку, на которой эта буква написана, при этом если эта буква написана первой, то кнопку нужно нажать один раз, если второй – то два раза и т.д. Устройство клавиатуры телефона приведено на рисунке. 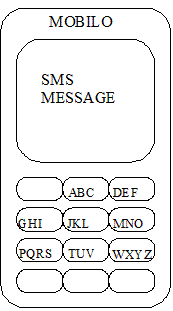
Таким образом, чтобы набрать слово SMS, нужно нажать следующие кнопки:
<PQRS> <PQRS> <PQRS> <PQRS> <MNO> <PQRS> <PQRS> <PQRS> <PQRS>
Для набора двух букв, которые находятся на одной кнопке, при наборе нужно сделать паузу между их вводом. Например, чтобы набрать BA, нужно два раза нажать кнопку <ABC>, затем сделать паузу и затем нажать кнопку <ABC> еще раз.
Если на кнопке написано три буквы, то как только эта кнопка нажата три раза подряд, последняя из написанных на ней букв сразу же добавляется в сообщение, а дальнейшие нажатия на эту кнопку воспринимаются как ввод следующей буквы. То же самое, если на кнопке написано 4 буквы. Таким образом, 4-х кратное нажатие на кнопку <ABC>, затем пауза, и затем нажатие на эту кнопку еще раз приведет к вводу текста CAA.
К сожалению, в силу произошедшего глюка, телефон стал иногда игнорировать паузы при вводе, а, иногда, наоборот, вести себя так, как будто была пауза тогда, когда паузы не было. Например, при вводе слова MOSCOW могло в итоге (как один из вариантов) получиться слово OMSCMNW.
Вы получили SMS-сообщение, набранное на этом телефоне. Известно, что изначально оно состояло из N символов. Напишите программу, которая определит количество вариантов исходных сообщений, которые при вводе могли превратиться в то, что вы получили (если вариантов окажется 0, то это будет означать, что у телефона сломалось что-то еще).
Сначала записана длина исходного сообщения N (1≤N≤80). Вторая строка содержит полученное SMS-сообщение – последовательность не более чем из 80 заглавных латинских букв.
Выведите одно число – количество вариантов исходного сообщения.
4 MAMA
1
2 WWW
2
10 MAMA
0
В тридесятом царстве в новогодние праздники все лягушки собираются на самом большом болоте, чтобы поиграть в замечательную игру. Всего в этом царстве живет N зеленых лягушек и M коричневых. Для игры они выбирают на болоте N + M + 1 кочку, на первые N кочек слева садятся зеленые лягушки, а на последние M — коричневые (т. е. между ними находится одна кочка, на которой никто не сидит). Зеленые лягушки садятся лицом к коричневым лягушкам, а коричневые — к зеленым. Кочки настолько маленькие, что развернуться на них, не свалившись в болото, совершенно не возможно. Поэтому лягушки могут двигаться только вперед и не могут разворачиваться.
На каждом ходе игры одна из лягушек перепрыгивает с той кочки, где она сидит, на свободную кочку. При этом лягушка может прыгнуть на соседнюю кочку вперед, либо перепрыгнуть через одну кочку, если соседняя занята.
Чтобы праздник удался, зеленые лягушки должны оказаться на последних кочках, а коричневые — на первых. Порядок, в котором лягушки окажутся на кочках, не важен. Так как на праздник каждый раз приходит разное количество лягушек, то им каждый год приходится придумывать очередность прыжков. Напишите программу, которая поможет лягушкам составить план прыжков.
Поиграть в эту игру для случая N=M=3 можно по ссылке:
Во входном файле записаны два числа N и M (1≤N≤1000, 1≤M≤1000) – количество зеленых и коричневых лягушек соответственно.
Выведите последовательность прыжков лягушек для достижения поставленной цели. Каждый прыжок можно задать одним числом — номером прыгающей лягушки (поскольку свободная кочка всегда ровно одна). Пронумеруем всех лягушек в соответствии с их начальным положением. Зеленые лягушки будут пронумерованы числами от 1 до N, а коричневые — с N+1 до N+M в порядке слева направо.
В первую строку выходного файла выведите число K — количество прыжков. K не должно превышать 107. Далее выведите K чисел — номера лягушек.
Если же достичь требуемой рассадки лягушек нельзя, выведите одно число –1.
2 1
5 2 3 2 1 3
Те, кто часто путешествуют самолетами, любят просить место у прохода. Ведь если сидеть у прохода, можно встать и прогуляться, не тревожа своих соседей.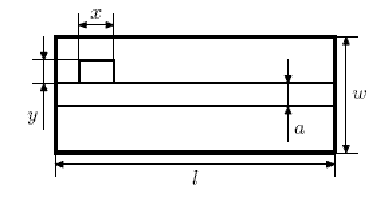
Компания «Аэротрам» готовит к производству новый самолет «T-239-n». Перед инженерами встала задача спланировать организацию салона, чтобы как можно больше мест было у прохода. Будем использовать следующую упрощенную математическую модель салона самолета. В горизонтальном сечении салон представляет собой прямоугольник длиной l и шириной w сантиметров. Кресло представляет собой прямоугольник размером x на y сантиметров и должно быть расположено в салоне так, чтобы его сторона длиной x была параллельна стороне салона длиной l. Проход представляет собой полосу шириной a, параллельную стороне салона длиной l. Проход идет вдоль всего салона.
В салоне требуется разместить n кресел. Помогите инженерам компании выяснить, как организовать салон, чтобы максимальное количество кресел было расположено у прохода. В салоне необходимо сделать хотя бы один проход. Кресло считается расположенным у прохода, если оно имеет хотя бы одну общую сторону с проходом.
Входной файл содержит шесть целых чисел: n, l, w, x, y и a (1 ≤ n ≤ 10000, 1 ≤ l,w,x,y,a ≤ 104).
Если разместить n кресел в салоне так, чтобы был хотя бы один проход, невозможно, выведите в выходной файл единственное число −1 . Иначе выведите максимальное количество кресел, которое можно разместить у прохода.
Комментарий к примерам тестов.
В первом примере оптимально расположить кресла, например, следующим образом:
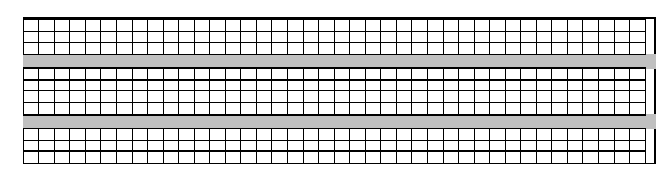
400 3250 750 80 60 70
160
450 3250 750 80 60 70
-1
Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины. 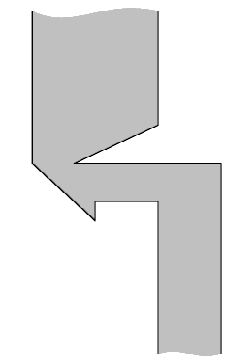
Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).
Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).
Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.
Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.
Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.
Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине
Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.
Оптимальное положение моста показано на следующем рисунке:
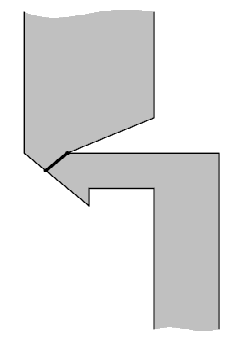
4 6 1 3 1 3 0 0 3 3 9 3 2 3 6 5
1.4142135623730951